Примеры решения задач

Задача 1. Среднее значение индукции в стальном листе толщиной

2b = 0,5 мм составляет В_ср = 1В*с/м²;  = 0,2 * 10⁷ Ом/м,  = 314 1/с.

По кривой намагничивания материала на постоянном токе найдено, что при В = 1 В*с/м², Н = 180 А/м. Определить удельные потери на вихревые токи.

Решение. Находим магнитную проницаемость

;

и

; ;

.

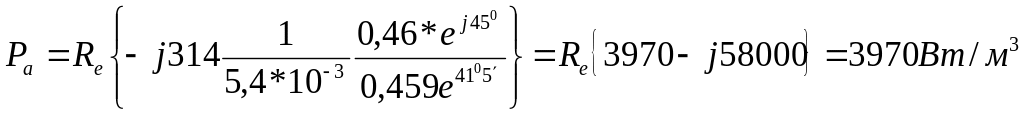Задача 2. По проводу течет ток I. Построить график изменения вектора Пойнтинга в пространстве вне провода, пренебрегая потерями энергии в проводе.

Решение. Определяем значение вектора Е и Н в пространстве вне провода: ,

Е_r 2r =  ( — заряд на единицу длины провода).

Вектор Пойнтинга - . Следовательно, S_z изменяется обратно пропорционально квадрату радиуса.

Заметим, что задача имеет смысл только для области вблизи провода, где можно пренебречь полем обратного провода.

Основные формулы.

Электромагнитные волны в диэлектрике:

Уравнения Максвелла для непроводящей среды ( = 0):

, ;

, .

Уравнение Максвелла в комплексной форме:

; ;

; .

Теорема Пойнтинга для диэлектрика без потерь:

.

Энергия электромагнитного поля:

.

Параметры волны:

коэффициент фазы - ;

длина волны - ;

волновое сопротивление - ;

фазовая скорость - .

Обобщенные (запаздывающие) электродинамические потенциалы:

; .

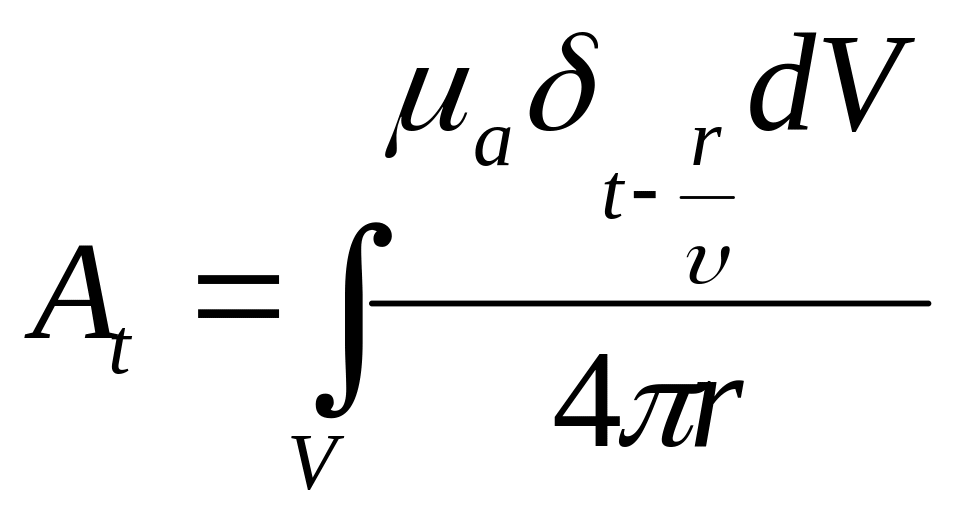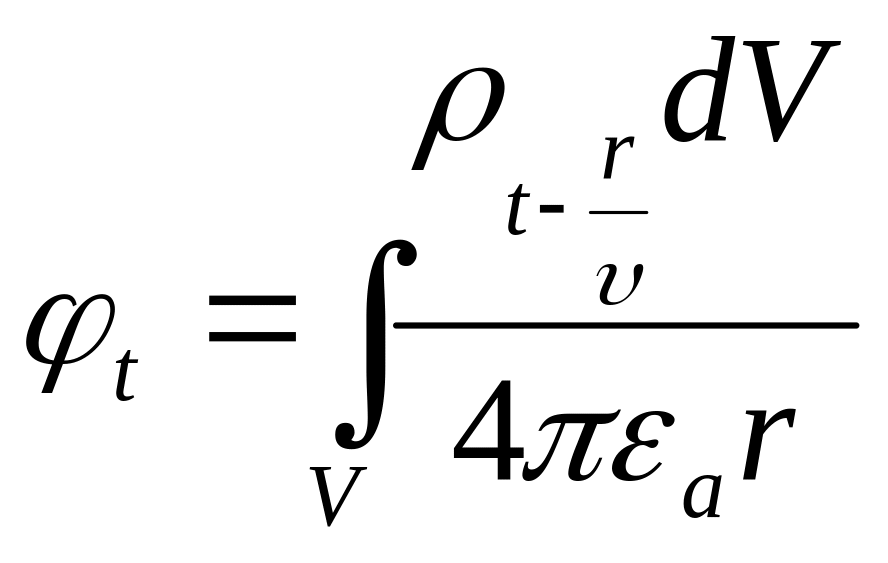Зависимость между векторами поля и обобщенными потенциалами:

; ;

.

Основные уравнения электромагнитного поля, выраженные через обобщенные потенциалы:

; .

Граничные условия в электромагнитном поле:

E_1t – E_2t = 0; D_1n – D_2n = ;

B_1n – B_2n = 0; H_1t – H_2t = 0.

Электромагнитные волны в несовершенном диэлектрике и в проводящей среде. Уравнения Максвелла:

, ;

; при _а = сonst.

Уравнения Максвелла в комплексной форме:

; ;

; .

Теорема Пойнтинга:

.

Граничные условия в электромагнитном поле:

E_1t – E_2t = 0; D_1n – D_2n = ;

B_1n – B_2n = 0; H_1t – H_2t =0.

Зависимость между векторами поля:

; ; .

Параметры волны:

коэффициент распространения - ;

коэффициент затухания - ;

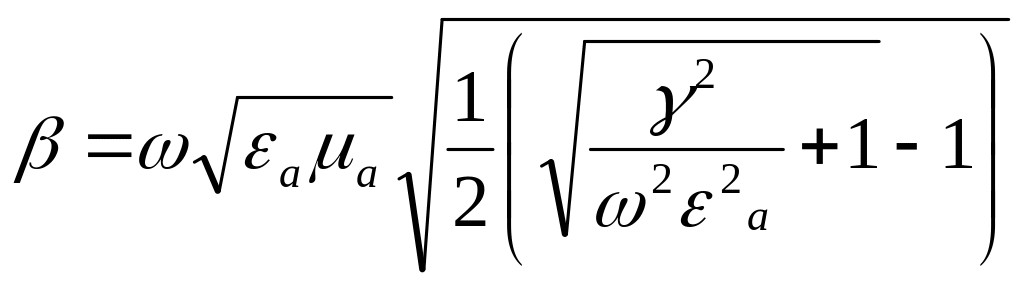коэффициент фазы - ;

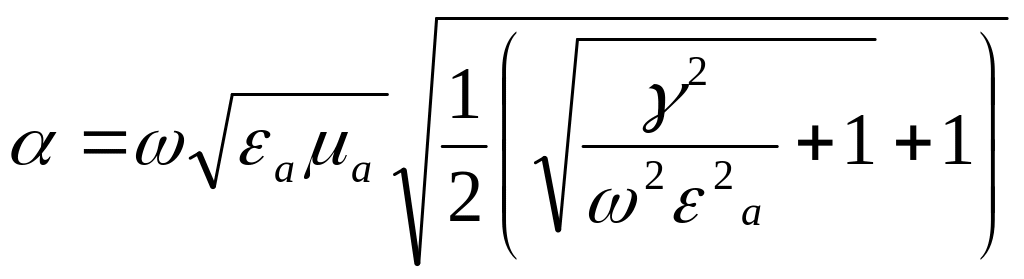волновое (характеристическое) сопротивление- ;

длина волны - ;

фазовая скорость - ;

групповая скорость - .

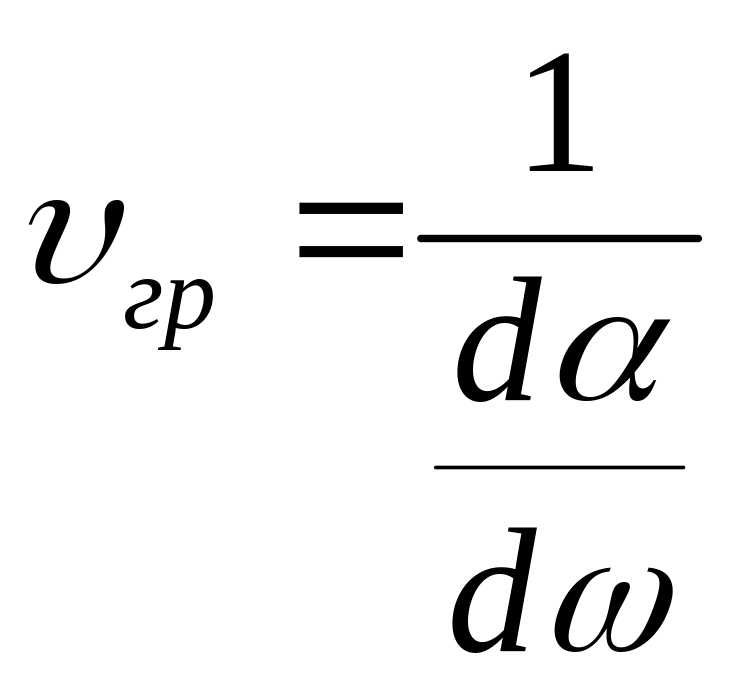Параметры волны в хорошо проводящей среде:

; ;

.

Эквивалентная глубина проникновения волны:

.

Далее приведены основные формулы векторного анализа.

Выражение вектора через проекции (декартовы прямоугольные координаты):

; ;

cos ; cos ; cos .

Сумма двух векторов: ;

S_x = A_x + B_x; S_y = A_y + B_y; S_z = A_z + B_z;

Разность двух векторов: ;

R_x = A_x - B_x; R_y = A_y - B_y; R_z = A_z - B_z;

Скалярное произведение двух векторов:

А*В = АВ cos (А, В) = A_xB_x + А_yВ_y + А_zВ_z.

Векторное произведение двух векторов:

,

где 1_n—единичный вектор по нормали к плоскости, в которой лежат перемножаемые векторы А и В.

Уравнение линии вектора А: ; .

Дифференциальный оператор Гамильтона — набла.

.

Сам вектор  не имеет реального значения, он приобретает определенный смысл лишь в комбинации со скалярными или векторными функциями.

.

Скалярное произведение  на вектор E:

.

Векторное произведение:

.

Градиент потенциала: ,

где 1_n—единичный вектор по нормали к поверхности  = const.

Свойства вихря вектора: divrot a = 0 rot(a + b) = rota + rotb,

rot(Ua) = Urota + gradUa, divab = brota – arotb.

Поток вектора через поверхность S: .

Дивергенция вектора: .

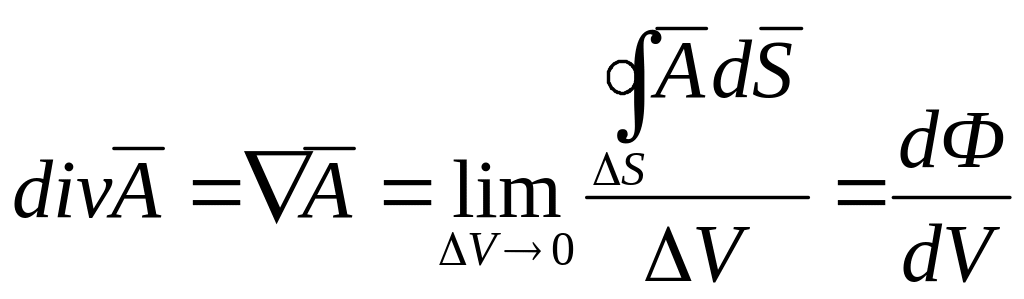Теорема Гаусса: .

Циркуляция вектора: .

Ротор вектора: .

Проекция ротора на направление n:

,

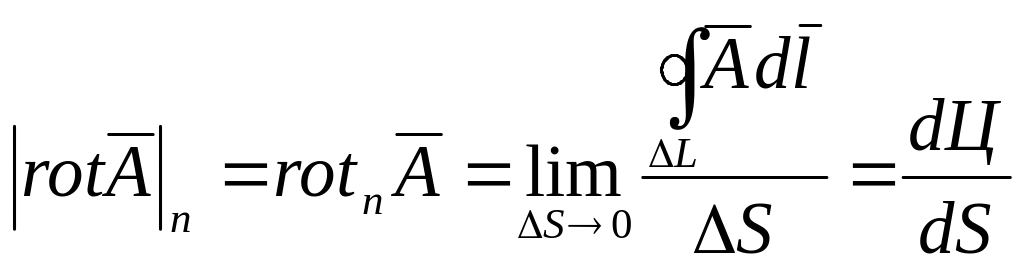где площадка S нормальна к направлению n.

Теорема Стокса: ,

где L—периметр поверхности S.

Лапласиан скаляра : .

Лапласиан вектора А: .

Ротор градиента: .

Дивергенция ротора: .

Дивергенция произведения скаляра и вектора:

.

Дивергенция векторного произведения: div[EH] = HrotE - ErotH.

Ротор от ротора: rot rot A = grad div A - ²A.