Абсолютные и стандартные энтропии

При абсолютном нуле энтропия идеального кристалла чистого вещества равна нулю (постулат Планка).

Справедливость постулата Планка, называемого третьим законом термодинамики, следует из экспериментальных данных о зависимости теплоемкости кристаллических веществ от температуры, а также из статистического характера второго закона термодинамики. При абсолютном нуле данное макросостояние кристалла чистого вещества, кристаллическая решетка которого не имеет каких–либо дефектов, предельно упорядочено и может быть реализовано единственным способом. Следовательно, термодинамическая вероятность при абсолютном нуле равна 1.

S = kln I

S = 0 (27)

На основании постулата Планка можно вычислить абсолютное значение энтропии. Зная, что dS= , a dQ = CdT, dS= , где С – молярная теплоемкость данного вещества. Интегрируя последнее уравнение в пределах от абсолютного нуля до Т, получим:

S_т = (28)

Энтропию S_T называют абсолютной энтропией, она численно равна изменению энтропии при равновесном переходе 1 моль кристаллического вещества от абсолютного нуля до данной температуры.

Вычисление абсолютной энтропии по уравнению (28) возможно лишь в том случае, если известна зависимость теплоемкости данного вещества от температуры.

Абсолютную энтропию тела в стандартном состоянии при данной «Т» называют стандартной энтропией и обозначают через ; чаще всего ее табулируют при 298,15К и обозначают через .

Важно подчеркнуть, что постулат Планка дает возможность вычислить абсолютное значение энтропий различного рода веществ при данном их состоянии, тогда как для других термодинамических функций, например, внутренней энергии и энтальпии могут быть определены только их изменения при переходе данной системы из одного состояния в другое.

Расчет изменения энтропии для протекании химического процесса

Изменение энтропии химического процесса равно алгебраической сумме стандартных энтропий участников реакции, с учетом их стехиометрических коэффициентов, причем энтропии продуктов реакции берутся со знаком плюс, а энтропии исходных веществ – со знаком минус.

Для реакции, протекающей по следующему уравнению: aA + bB  mM + nN

S = (m + n ) – (a ) (29)

Например, изменение энтропии реакции

H₂(г) + Cl₂(г) = 2HCl(г)

если (г) = 130,6 Дж.моль^–1К^–1; (г) = 36,69 Дж.моль^–1К^–1;

(г) = 186,70 Дж.моль^–1К^–1

в соответствии с уравнением (29) равно:

S = 2186,70 – 130,6 – 36,69 = 206,11 Дж.моль^–1К^–1;

Энергия Гиббса

По изменению энтропии можно судить о направлении и пределах протекания процессов только в изолированных системах. В случае закрытых и открытых систем необходимо также учитывать изменение энтропии окружающей среды. Решение последней задачи или крайне сложно, или невозможно. Поэтому в термодинамике для изучения открытых или закрытых систем используют другие термодинамические функции – так называемые термодинамические потенциалы, изменение которых позволяет определять направление процессов и пределы их протекания без учета изменений их в окружающей среде. В частности, к термодинамическим потенциалам относится функция состояния, называемая энергией Гиббса, которую обозначают через G. Понятие об энергии Гиббса было введено на основе объединенного уравнения первого и второго законов термодинамики. Объединенное уравнение может быть выведено следующим образом.

Из первого закона термодинамики следует:

A = Q – U (30).

Из второго закона термодинамики получаем для обратимого процесса:

Q = TS (31)

для необратимого процесса: Q < TS (32)

Подставляя значение Q из уравнения (31) и уравнения (32) в уравнение (30) находим:

для обратимого процесса А обр. =TS – U (33)

для необратимого процесса Анеобр. = < TS – U (34)

Уравнение (33) называют объединенным уравнением первого и второго начал термодинамики для обратимых процессов. Так как внутренняя энергия и энтропия являются функциями состояния, то их изменение не зависит от того, как протекает данный процесс, обратимо или необратимо, следовательно:

ТS обр. – Uобр. = TSнеобр. – Uнеобр. и Аобр. > Анеобр. т.е. работа, совершаемая при обратимом процессе, больше работы, производимой системой при необратимом процессе при условии, что начальное и конечное состояния системы одинаковы в обоих случаях. Имея в виду, что работа, производимая системой, при обратимом процессе является максимальной для данного изменения состояния системы, преобразуем уравнение (33):

Amax = T(S₂ – S₁) – (U₂ – U₁)

Группируя величины с одинаковыми индексами, получаем:

Amax = (U₁ – TS₁) – (U₂ – TS₂) (35)

т.к. U и S – функции состояния, то величина (U – TS) должна быть также функцией состояния.

Если система, кроме полезной работы, совершает работу, против силы внешнего давления (p = const), то для обратимого процесса Amax = Аmax + pV

или Аmax = Amax – pV, где Аmax – максимальная полезная работа, совершаемая системой в обратимом изобарно–изотермическом процессе. Из уравнения (35) получаем для обратимого процесса:

Amax = TS – U –pV (36)

для необратимого процесса: Amax < TS – U –pV (37)

учитывая, что V =V₂ – V₁, получаем:

Аmax = U₁ – U₂ + TS₂ – TS₁ – pV₂ + pV₁

Группируя величины с одинаковыми индексами, находим:

Аmax = (U₁ – TS₁ + pV₁) – (U₂ – TS₂ + pV₂) (38)

Величину (U – TS + pV), которая является функцией состояния, т.к. U,S и V суть функции состояния, называют энергией Гиббса и обозначают через G. Раньше эту функцию состояния называли изобарно–изотермическим потенциалом.

Таким образом,

G = U – TS + pV (39)

Имея в виду последнее уравнение, можно записать:

Аmax = G₁ – G₂ т.к.

G = G₂ – G₁, Аmax = –G (40)

Из уравнения (40) следует, что максимальная полезная работа, совершаемая системой в обратимом изобарно–изотермическом процессе, равна уменьшению энергии Гиббса. Для необратимого процесса, путем аналогичного преобразования справедливо:

Анеобр. < – G (41),

т.е. уменьшение энергии Гиббса в необратимом процессе больше производимой системой полезной работы.

Зная, что U + pV = Н, уравнение (40) можно переписать следующим образом:

G = H – TS (42)

или

G = H – TS (43)

Последнее уравнение может быть представлено следующим образом:

G = U + pV – TS

или

U = G – pV + TS,

из чего следует, что изменение внутренней энергии системы можно представить как сумму трех слагаемых: G – часть внутренней энергии системы, способная при изобарно–изотермических условиях превратиться в работу, pV – часть внутренней энергии, затрачиваемая системой на совершение работы против сил внешнего давления, и TS – «связанная энергия», представляющая собой часть внутренней энергии, которая в указанных условиях не может быть превращена в работу. «Связанная энергия» тем больше, чем больше энтропия данной системы. Таким образом, энтропию можно рассматривать как меру «связанной энергии».

Из уравнений (40 и 41) следует, что величина G служит мерой способности системы производить работу и поэтому решить вопрос, может ли реакция протекать самопроизвольно. Реакция протекает самопроизвольно только в том случае, если происходит уменьшение энергии Гиббса системы. Такие реакции называют экзергоническими, если же энергия Гиббса системы возрастает, то для осуществления реакции необходимо затратить работу. Такие реакции называют эндергоническими.

Реакцию, которая в данных условиях не является самопроизвольной, поскольку протекание ее связано с увеличением «свободной энергии», можно осуществить путем сопряжения ее с другой реакцией, характеризующейся достаточно большой отрицательной величиной изменения энергии Гиббса. Условием такого сопряжения будет наличие интермедиата, т.е. общего для обоих реакций вещества.

1. А + В ⇄ С + Д > 0

2. Д + К ⇄ М + Г < 0

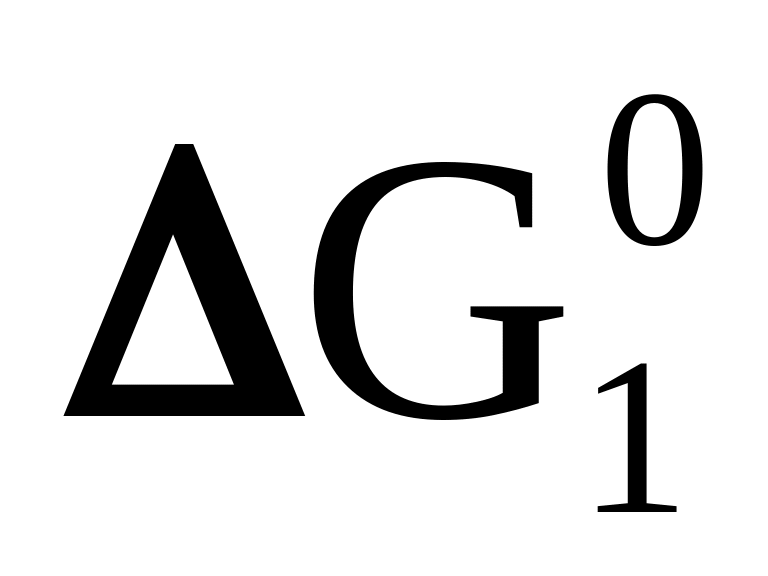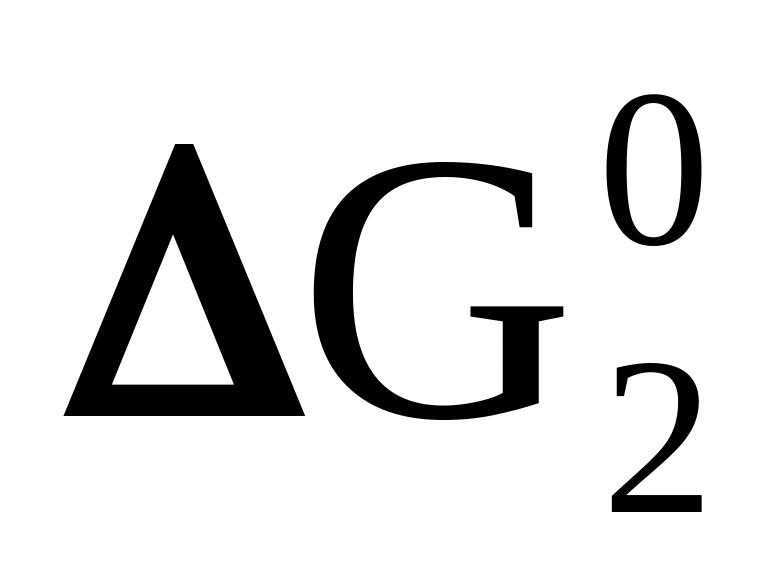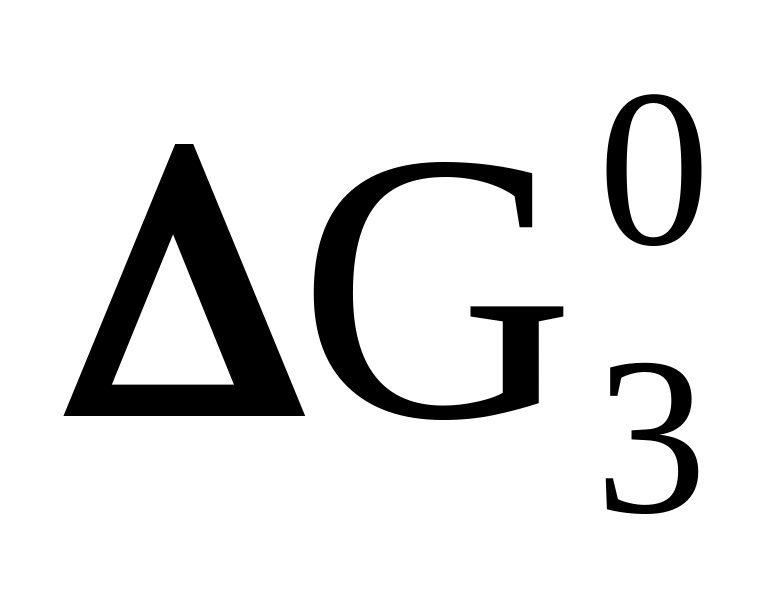3. А + В + К ⇄ С + М + Г < 0

Для живых организмов можно привести много примеров сопряженных реакций. Особенно большое значение имеют реакции гидролиза таких соединений, как аденозинтрифосфат (АТФ), аденозиндифосфат (АДФ), аргининфосфат, креатинфосфат, характеризующиеся величинами изменения энергии Гиббса от – 29,99 до – 50,21 кДж/моль.