Шаг Жордановых исключений осуществляется по следующим правилам:

1. Ноль первого столбца в строке разрешающего элемента меняется местами с переменной .

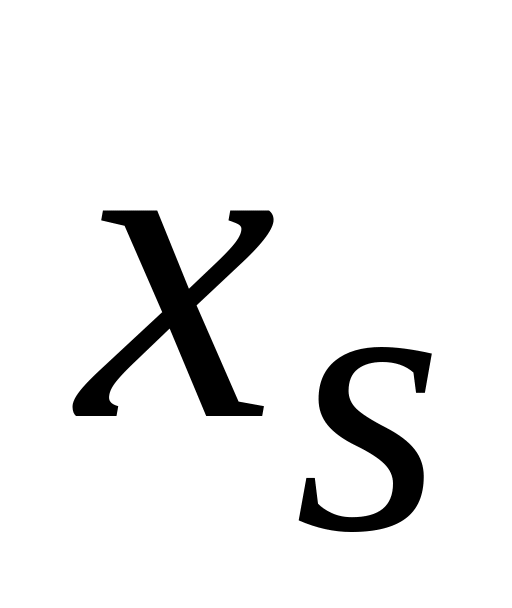2. Разрешающий элемент заменяется обратной величиной.

3. Остальные элементы разрешающей строки делятся на разрешающий элемент.

4. Остальные элементы разрешающего столбца делятся на разрешающий элемент и меняют знак на противоположный.

5. Прочие элементы вычисляются по формуле

.

Или диагональ прямоугольника, на которой расположен разрешающий элемент и преобразуемый элемент , назовем главной, а другую диагональ – побочной. Тогда преобразованный элемент равен разности произведений элементов, расположенных на главной и побочной диагоналях, деленной на разрешающий элемент.

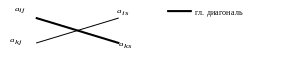
6. 0-столбцы вычеркиваются.

Если система ограничений совместна, то через некоторое число шагов все нули в левом столбце будут замещены переменными . Тогда начальный опорный план найдем, приравняв свободные переменные к нулю, а базисные (столбец «БП») – к соответствующим свободным членам (столбец 1).

Если в ходе Жордановых преобразований встретится 0-строка, в которой все элементы неположительные, то данная система не имеет неотрицательных решений, хотя и является совместной.

Допустим, после некоторого числа шагов Жордановых преобразований все нули в левом столбце замещены переменными , т.е. получили таблицу 5.

Таблица 5

		СП
БП	1		…		...
			…		...
...	...	...	…	...	...	...
			…		...
...	...	...	…	...	...	...
			…		...
			…		...

Тогда компоненты начального опорного плана будут

БП: ,…, ,…, ,

СП: .

Таким образом, начальный опорный план и значение целевой функции на этом плане .

Например, найдем начальный опорный план ЗЛП примера 2-м методом Жордановых исключений. Представим каноническую запись (см. пример 5) в виде (2.11)-(2.12), т.е.

;

Здесь в третьем и четвертом ограничениях предпочтительные переменные и оставлены в левой части.

Заполним первую Жорданову таблицу (таблица 6).

Таблица 6

		СП
БП	1					отношения
0=	31	5	0	4	0	31/5
0=	36	0	3	0	6
	10	1	1	0	0	10/1
	10	0	0	1	1
	0	–8	–7	–4	–2

Начальный опорный план будет найден, если в первом столбце таблицы все нули в ходе преобразований Жордана будут заменены переменными .

Пусть -столбец будет разрешающим. Для нахождения разрешающей строки составим отношения свободных членов к соответствующим положительным элементам этого столбца. Так как в этом столбце только два положительных элемента 5 и 1, то отношения будут и . Так как , то элемент «5» и будет разрешающим. Шаг Жордановых исключений относительно найденного разрешающего элемента переводит таблицу 6 в таблицу 7.

Таблица 7

		СП
БП	1	0	x12	x21	x22
x11=	31/5	1/5	0/5	4/5	0/5
0=	(365–310)/5	0	(35–00)/5	(05–40)/5	(65–00)/5
x3=	(105–311)/5	–1/5	(15–01)/5	(05–41)/5	(05–01)/5
x4=	(105–310)/5	0	(05–00)/5	(15–40)/5	(15–00)/5
Z	(05–31(–8))/5	8/5	(–75–0(–8)/5	(–45–(4(–8)) /5	(–25–0(–8))/5

Вычеркивая 0-столбец, получим таблицу 8.

Таблица 8

		СП
БП	1	x12	x21	x22
x11=	6,2	0	0,8	0
0=	36	3	0	6
x3=	3,8	1	–0,8	0
x4=	10	0	1	1
Z	49,6	–7	2,4	–2

Пусть теперь разрешающим будет -столбец. Найдем отношения свободных членов к соответствующим положительным элементам этого столбца - и (таблица 9).

Таблица 9

		СП
БП	1				отношения
	6,2	0	0,8	0
0=	36	3	0	6	36/6
	3,8	1	–0,8	0
	10	0	1	1	10/1
	49,6	–7	2,4	–2

Так как , то вторая строка будет разрешающей. Итак, следующий разрешающий элемент будет 6, и шаг Жордановых исключений переводит таблицу 9 в таблицу 10.

Таблица 10

		СП
БП	1	x12	x21	0
x11=	6,2	0	0,8	0
x22=	6	0,5	0	1/6
x3=	3,8	1	–0,8	0
x4=	4	–0,5	1	–1/6
Z	61,6	–6	2,4	2/6

Вычеркивая 0-столбец, получим таблицу 11.

Таблица 11

		СП
БП	1	x12	x21
x11=	6,2	0	0,8
x22=	6	0,5	0
x3=	3,8	1	–0,8
x4=	4	–0,5	1
Z	61,6	–6	2,4

Найдем начальный опорный план, приравняв свободные переменные к нулю, т.е. , а базисные переменные к свободным членам, т.е. .

Значит, начальный опорный план: . На этом плане целевая функция: .

Итак, благодаря преобразованиям Жордана, исходную задачу мы можем записать (исходя из последней таблицы) в виде

;