
- •Программа дисциплины
- •Тема 1 общая характеристика и классификация математических методов и моделей, применяемых в экономических исследованиях Предмет математического программирования
- •Общая схема формирования экономико-математической модели
- •Классификация методов математического программирования
- •Тема 2 линейное программирование Задача линейного программирования (злп)
- •Формы записи задач линейного программирования
- •Приемы, позволяющие переходить от одной формы записи условий задач к другой
- •Графический метод решения злп
- •Симплекс-метод решения злп
- •Алгоритм симплекс-метода
- •Геометрическая интерпретация в случае двух переменных
- •Отыскание начального опорного плана (1-ый пункт алгоритма)
- •Отыскание начального опорного плана методом искусственного базиса
- •Отыскание начального опорного плана путем преобразования таблицы Жордана
- •Шаг Жордановых исключений осуществляется по следующим правилам:
- •Исследование на оптимальность опорного плана при минимизации целевой функции (второй пункт алгоритма)
- •Переход к новому, нехудшему опорному плану (третий пункт алгоритма)
- •Тема 3 транспортная задача линейного программирования Постановка транспортной задачи по критерию стоимости в матричной форме
- •Закрытая и открытая модели транспортной задачи
- •Алгоритм решения сбалансированной транспортной задачи
- •Построение исходного опорного плана (первый пункт алгоритма)
- •Проверка на оптимальность невырожденного опорного плана методом потенциалов (второй пункт алгоритма)
- •Переход к нехудшему опорному плану (третий пункт алгоритма)
- •Цикл пересчета
- •Тема 4 динамическое программирование
- •I этап. Условная оптимизация
- •II этап. Безусловная оптимизация
- •Задача об оптимальной стратегии замены оборудования
- •I этап. Условная оптимизация
- •II этап. Безусловная оптимизация
- •Литература
- •Тема 1 общая характеристика и классификация математических методов и моделей, применяемых в экономических исследованиях 3
- •Тема 2 линейное программирование 6
- •Тема 3 транспортная задача линейного программирования 33
- •Тема 4 динамическое программирование 50
Формы записи задач линейного программирования
Симметричной (стандартной) формой записи ЗЛП называется задача максимизации целевой функции (2.1) при ограничениях вида (2.2) и (2.5) или задача минимизации целевой функции (2.1) при ограничениях вида (2.4) и (2.5), т.е.
![]() ;
;
![]() ,
,
![]()
или
![]() ;
;
![]() ,
,
,
где ![]() – заданные действительные числа.
– заданные действительные числа.
Канонической формой записи ЗЛП называется задача минимизации или максимизации целевой функции (2.1) при ограничениях вида (2.3) и (2.5), т.е.
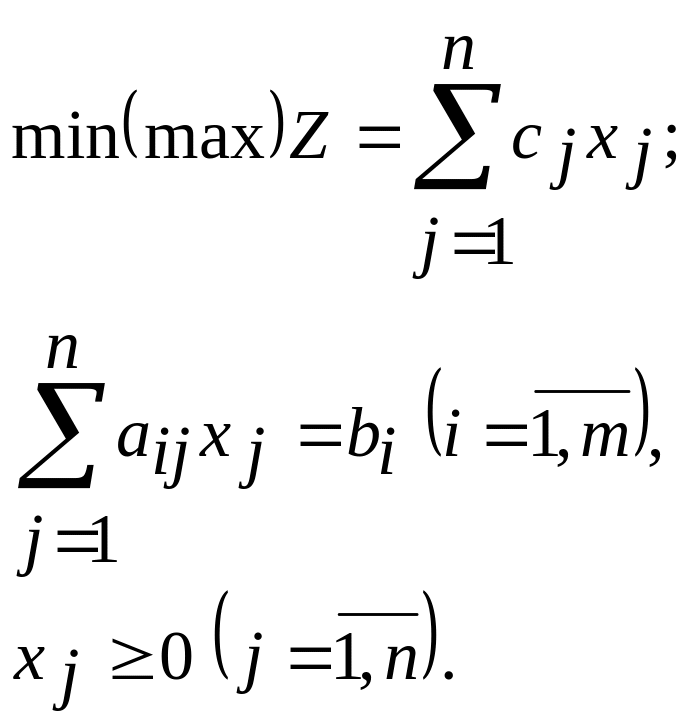
Приемы, позволяющие переходить от одной формы записи условий задач к другой
Переход от задачи на минимум к задаче на максимум осуществляется умножением целевой функции на «–1». Действительно, если функция
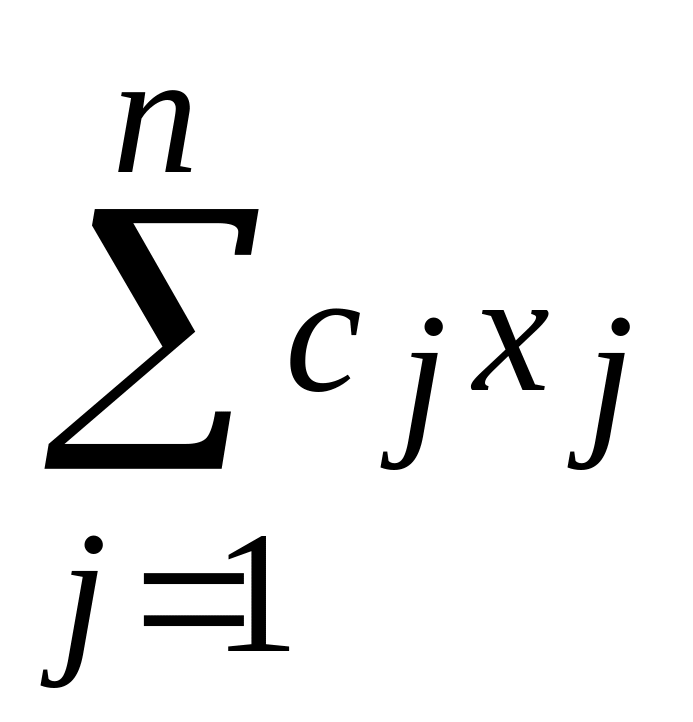 достигает минимума при значениях
достигает минимума при значениях
 ,
то функция
,
то функция
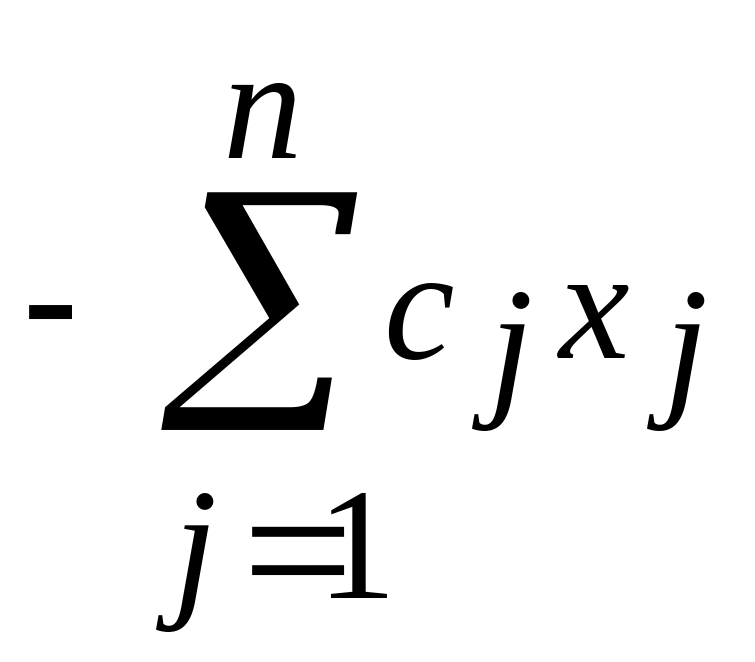 достигает
при тех же значениях переменных
максимума.
достигает
при тех же значениях переменных
максимума.
Переход от неравенства вида к неравенствам вида (и наоборот) также осуществляется умножением исходного неравенства на –1.
Переход от неравенства к равенству осуществляется введением дополнительной неотрицательной переменной
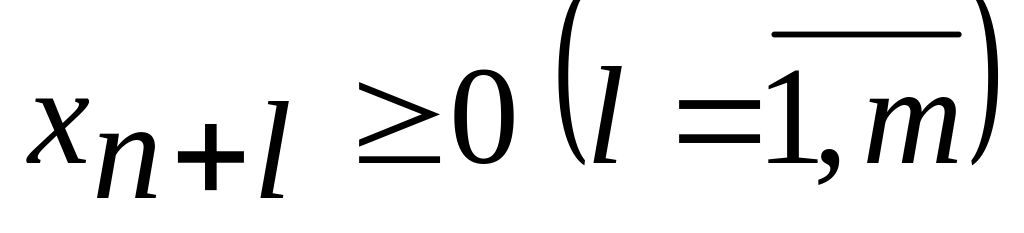 .
К примеру, если первое ограничение
имеет вид
.
К примеру, если первое ограничение
имеет вид
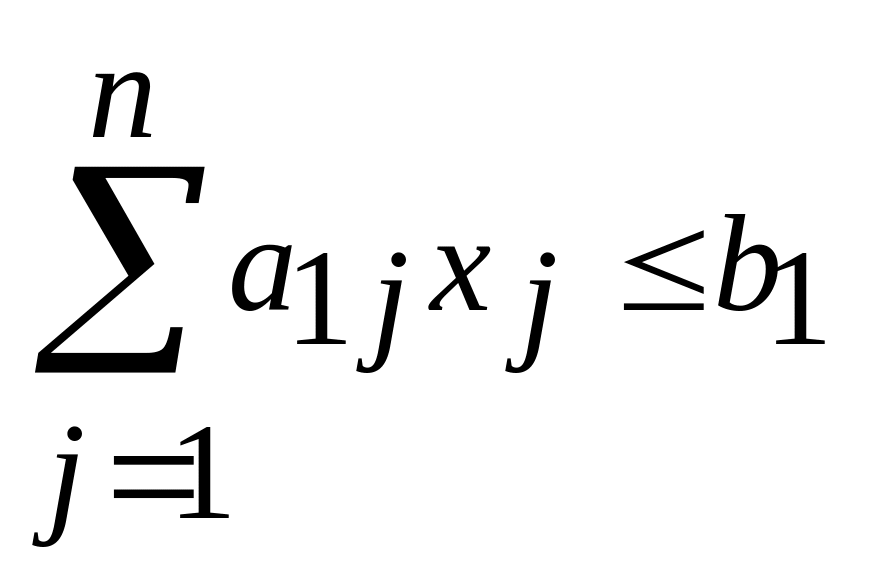 ,
то, вводя неотрицательную переменную
,
то, вводя неотрицательную переменную
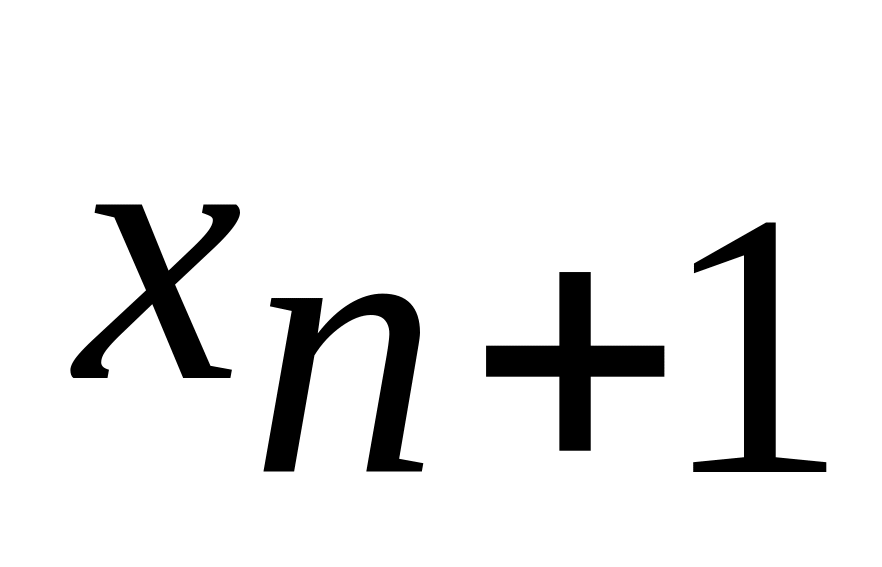 ,
получим
,
получим
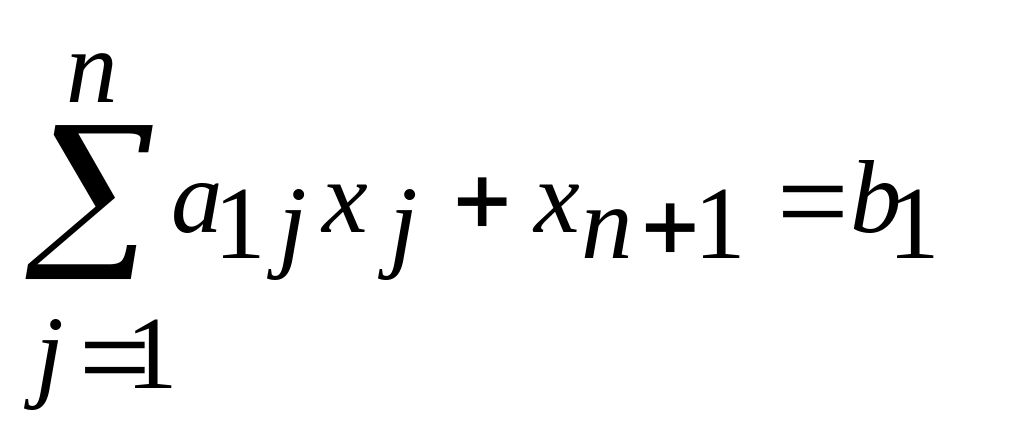 ,
если второе ограничение имеет вид
,
если второе ограничение имеет вид
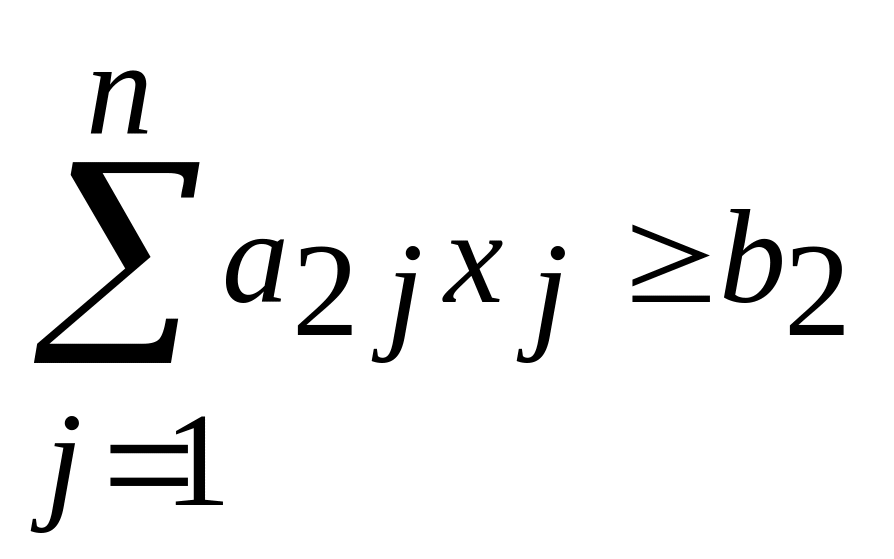 ,
то, вводя неотрицательную переменную
,
то, вводя неотрицательную переменную
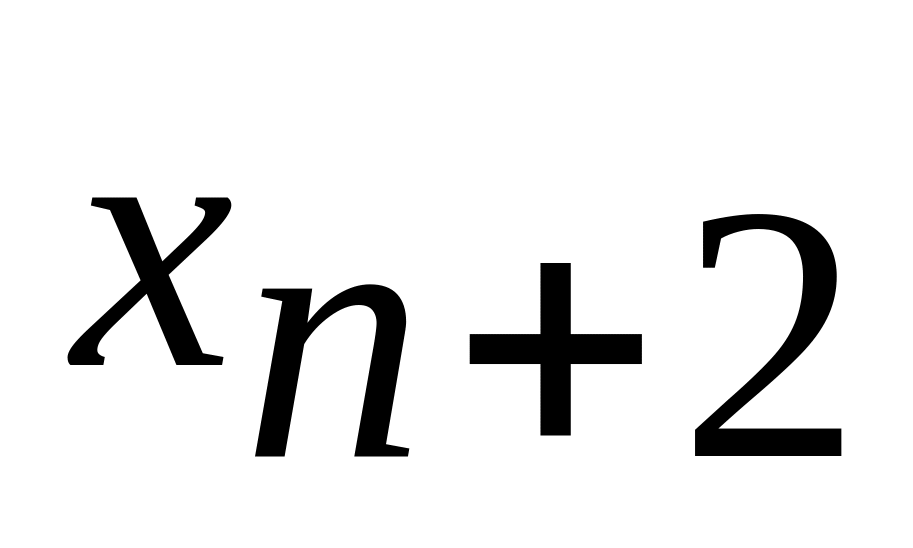 ,
получим
,
получим
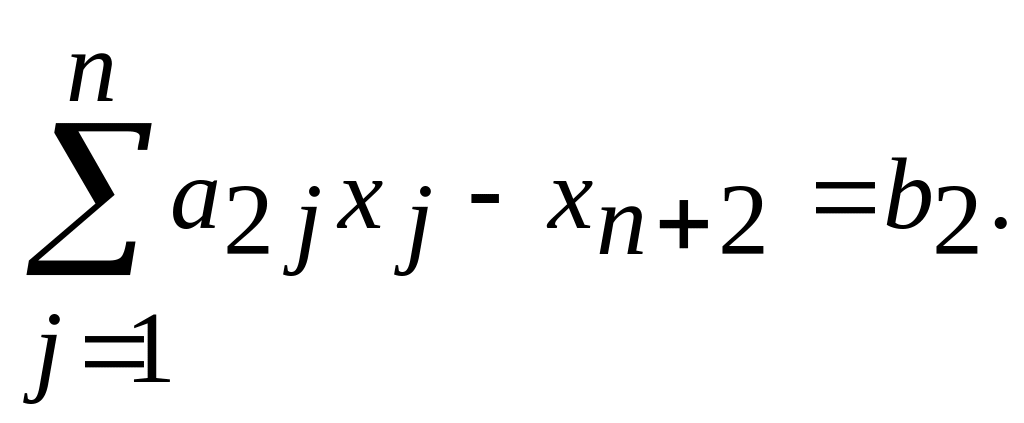
При переходе от равенств к неравенствам можно руководствоваться следующим: если дано А=B, то это можно формально записать в виде двух неравенств А В, А В;
Введение условий неотрицательности переменных. Пусть на переменную
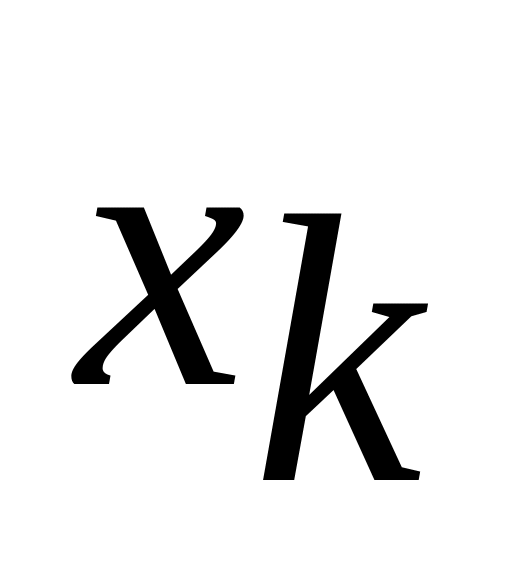 это условие не было наложено, тогда
вместо этой переменной можно ввести
две неотрицательные переменные
это условие не было наложено, тогда
вместо этой переменной можно ввести
две неотрицательные переменные
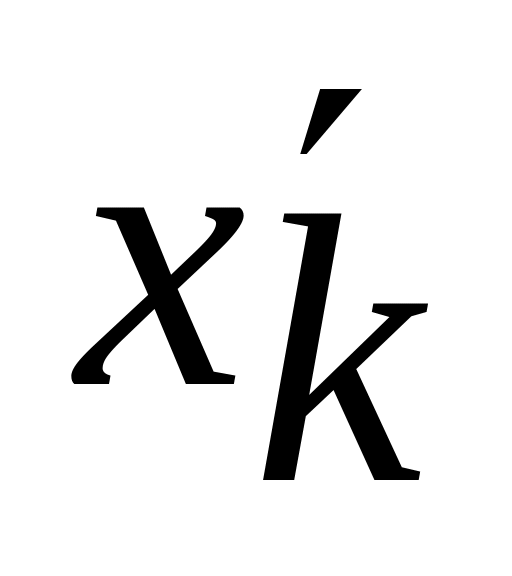 и
и
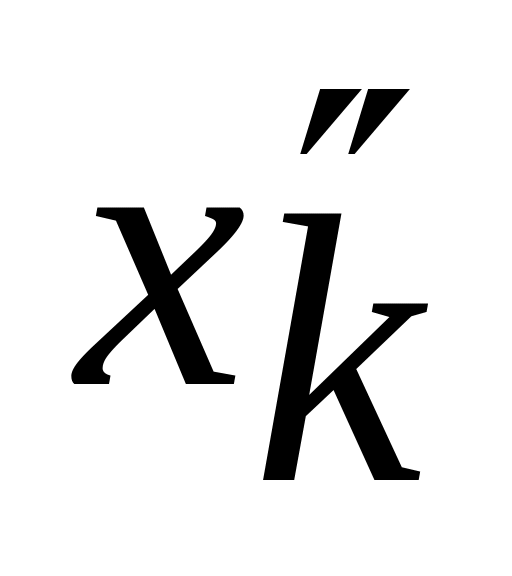 и представить
и представить
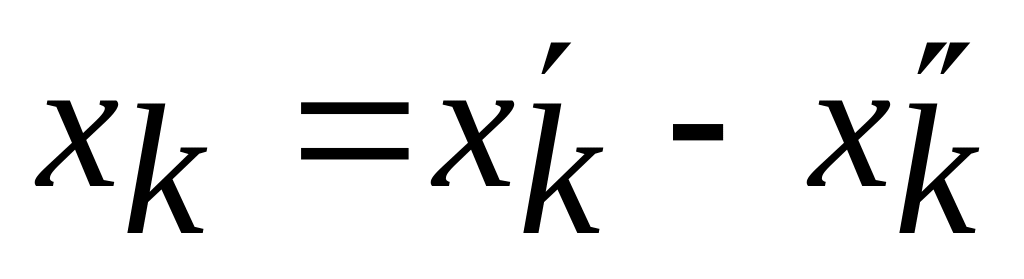 ,
где
,
где
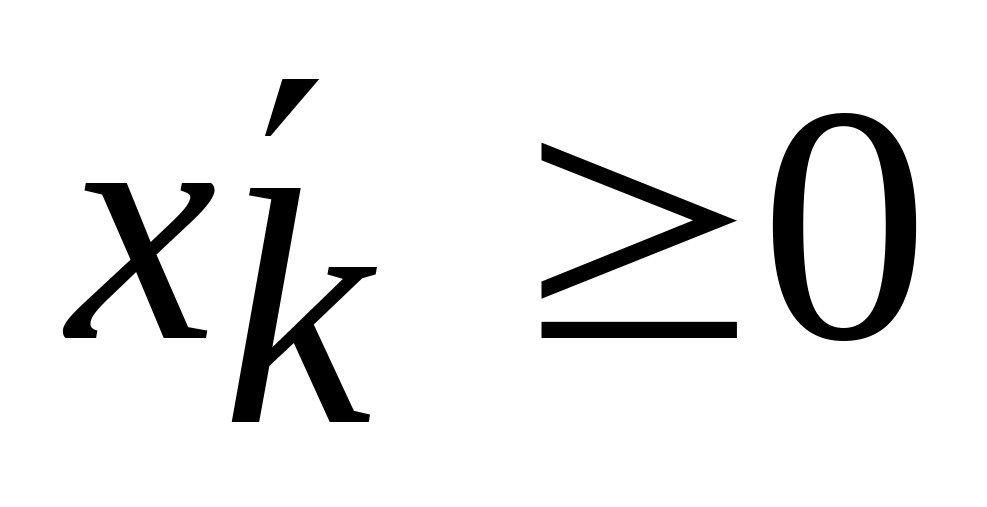
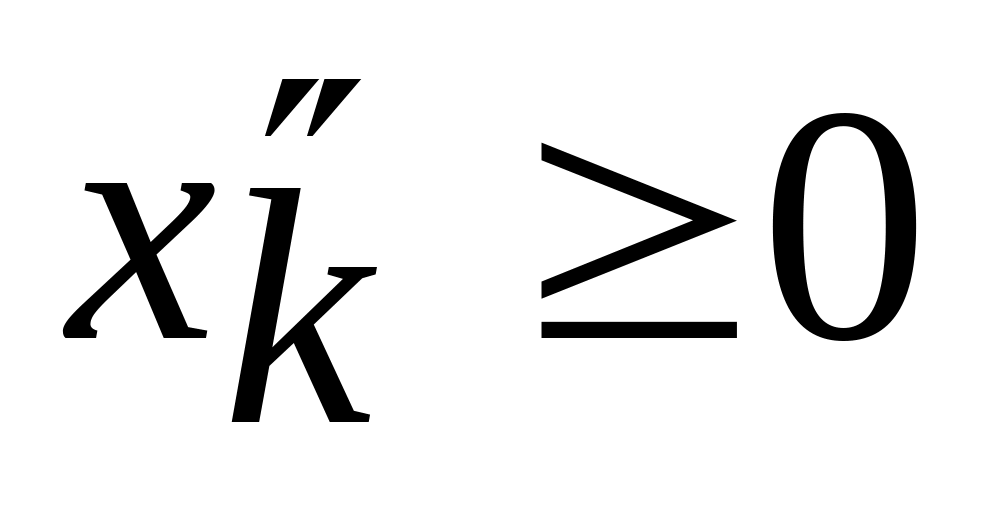 .
Это всегда возможно.
.
Это всегда возможно.
Изложенными приемами общая ЗЛП может быть сведена к симметричной и канонической формам записи ЗЛП и наоборот. Однако, поскольку в процессе таких преобразований мы вводили дополнительные переменные, то после того, как задача решена, нужно произвести обратный переход к исходным переменным, определяющим непосредственный экономический смысл задачи.
Пример 4
Пусть математическая модель задачи имеет следующий вид
![]() ;
;
![]()
Для получения
общей задачи линейного программирования
необходимо, чтобы на все переменные
было наложено условие неотрицательности.
Для наложения этого ограничения на
переменную
воспользуемся правилом 5. Введем новые
неотрицательные переменные
![]() и
и
![]() и представим
и представим
![]() ,
где
,
где
![]() и
и
![]() .
.
Тогда ОЗЛП будет иметь вид
![]() ;
;
![]()
или (раскрыв скобки):
![]() ;
;
![]()
В симметричной (стандартной) форме записи задача будет иметь вид
;
![]()
Здесь ограничение (2.6) умножено на –1, а ограничение (2.7) заменено двумя ограничениями:
![]()
откуда, домножив второе ограничение на –1, получим ограничение (2.9) вида .
Таким образом, из ограничения (2.7) получены ограничения (2.8) и (2.9).
В канонической форме записи ЗЛП будет иметь вид
;
![]()
Пример 5
Экономико-математическую модель задачи, составленную в примере 2, представим в канонической форме записи:
![]() ;
;
![]()
Введенные дополнительные переменные и имеют экономический смысл, связанный с содержанием задачи. Здесь , – время простоя оборудования А1 и А2 соответственно.
