§ 1. Основные понятия

п-местным отношением R на множествах А₁,…,А_n называется подмножество прямого произведения

A₁x...xA_n.

Другими словами, элементы х₁,…, х_п (где х₁ А₁, ...) связаны отношением R тогда и только тогда, когда (x₁,x₂,…, x_n) R ((x₁,x₂,…, x_n)— упорядоченный набор из п элементов).

Наиболее часто встречаются отношения при п = 2; в этом случае они называются бинарными отношениями. Следовательно, бинарное отношение между множествами А и В является просто подмножеством АxВ. Если эти множества эквивалентны (скажем, равны А), то будем говорить, что подмножество А² определяет отношение на А.

Отношения не являются чем-то новым. Можно по­строить отношения, которые, несомненно, будут знакомы читателю. Рассмотрим следующие примеры.

Пример 1.1. Пусть

А = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.

Тогда R = {(х, у): х, у А, х — делитель у и х ≤ 5} мо­жет быть записано в явном виде:

R = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5),

(1, 6), (1, 7), (1, 8), (1, 9), (1, 10),

(2, 2), (2, 4), (2, 6), (2, 8), (2, 10),

(3, 3), (3, 6), (3, 9),

(4, 4), (4, 8),

(5, 5), (5, 10)}. //

Пример 1.2 (шахматы). Как и выше, пусть

F = {а, b, с, d, е, f, g, h}, R = {1, 2, 3, 4, 5, 6, 7, 8}

и пусть S = FxR.

Таким образом, S — множество всех клеток, обознача­емых парами (х, у), где x F, у R. Определим бинар­ное отношение С (для ладьи!) на S так, что (s, t) C тогда и только тогда, когда s и t — элементы S и ладья может пройти от s к t одним ходом на пустой доске. (На­помним, что ладья может изменять либо горизонтальную координату, либо вертикальную, но не обе координаты одновременно.) Поэтому С S x S и

C = {((f_S, r_S), (f₁, r₁)): (f_S = f₁ и r_S ≠ r₁)

или (f_S ≠ f₁ и r_S = r₁)}. //

На первый взгляд определение С может выглядеть сложно, но внимательное исследование показывает, что значение отношения находится непосредственно и вся необходимая информация содержится в определении.

В общем случае ряд различных отношений на мно­жестве А зависит от |А|. Большая часть этих отношений не представляет особого интереса. Ниже приведены три отношения, которые полезны при рассмотрении множеств.

Определение. Для любого множества А опреде­лим тождественное отношение I_А и универсальное отно­шение U_A следующим образом:

I = {(a, а): а А), U = {(a, b): а А, b А}.

Таким образом, U_A = A². Так как ø A², то ø является отношением на A и называется пустым отношением. //

Пусть отношение R определено в соответствии с изо­бражением на рис. 2.1. Необходимо сконцентрировать на­ше внимание на том, что происходит на концах R, т. е. рассмотреть элементы А и В, которые принадлежат R. Они являются элементами подмножеств А и В соответ­ственно и, как следовало ожидать, имеют специальные названия.

Определение. Свяжем с каждым бинарным отно­шением R между А и В два множества — область опре­деления D(R) и область значений (R). Они определя­ются следующим образом:

D(R)={x: (x,y) R}, (R)={y: (x,y) R). //

Пример 1.3. Пусть отношение R такое же, как и в примере 1.1. Тогда

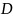(R)= {1, 2, 3, 4, 5}, (R) = А. //

Пример 1.4. Предположим, что мы имеем некото­рую программу. Она читает два числа из множества А = {1, 2, 3, 4, 5}, обозначаемых х и у, и, если х<у, печа­тает число z (также из А) такое, что х ≤ z < у. В любом случае программа останавливается после считывания всех чисел из А.

Задача определяет отношение Р, Р АxА такое, что

P = {((x, y), z): x < y, x ≤ z < y}.

Не все входные данные приводят к выдаче результата. Поэтому область определения Р не совпадает с А². Ясно, что

Р = {((1, 2), 1), ((1, 3), 1), ((1, 3), 2),

((1, 4), 1), ((1, 4), 2), ((1, 4), 3),

((1, 5), 1), ((1, 5), 2), ((1, 5), 3), ((1, 5), 4),

((2, 3), 2), ((2, 4), 2), ((2, 4), 3),

((2, 5), 2), ((2, 5), 3), ((2, 5), 4),

((3, 4), 3), ((3, 5), 3), ((3, 5), 4),

((4, 5), 4)};

(P)={(1, 2), (1, 3), (1, 4), (1, 5),

(2, 3), (2, 4), (2, 5),

(3, 4), (3, 5),

(4, 5)};

(Р)={1, 2, 3, 4}. //

Хотя каждое отношение является множеством и мо­жет быть обозначено прописной буквой, существует так­же практика обозначения отношений строчными гречески­ми буквами, например 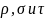. Часто используют следу­ющие обозначения:

а) (а, b) р, т. е. (а, b) находится в ;

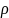б) а b, а связано с b отношением ;

в) b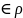 (a).

Первое из обозначений является естественным (оно следует из определений теории множеств). Второе де­лается более разумным, если мы рассмотрим отношение порядка (которое будет определено несколько ниже), где

R N² иR={(x, у): х<у}.

Здесь вместо 6R7 мы можем написать 6 < 7; следова­тельно, мы разрешаем запись любого отношения с ис­пользованием рассмотренных выше символов, если результирующая последовательность символов будет од­нозначно определенной. Третья форма записи является новой и будет преобразована к более привычным обозна­чениям в гл. 3. Из заданного бинарного отношения мож­но вывести ряд других отношений, большинство из кото­рых будут обратными отношениями.

Определение. Пусть R — бинарное отношение. Определим обратное отношение R ^-1 следующим образом:

R ^-1={(x, у):(у, x) R}.

Таким образом, R ^-1 связывает те же пары элементов, что и R, но «в другом порядке». //

Следовательно, если R А x В, то

R ^-1 Bx, (R ^-1) = (R) и (R ^-1) = (R).

Чтобы избежать использования большого количества ско­бок, будем также использовать обозначения _R и _R вме­сто (R) и (R) соответственно.

Упражнение 2.1.

1. Пусть Х = {2, 4, 6, 8) и = {(х, у): х, у Х и х < у). Выписать все элементы и ^-1.

2. Пусть ξ = 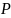({а, b, с}). Найти все элементы отно­шений 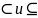на ξ.

3. Пусть ξ = Z² и = {(x, у): х < у}. Описать ' — дополнение — без использования отрицания отношения «меньше».

4. Пусть 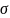= {(х, у): x y}. Может ли ' быть опи­сано тем же способом, что и ' в 2.1, 3? Ответ проверьте.

5. На улице есть 30 домов, пронумерованных обычным способом: нечетные номера с одной стороны, а четные с другой. Пусть h_n обозначает жителя, живущего в доме с номером п. Описать при помощи символов отношение N на множестве жителей такое, что h₁ находится в отно­шении N к h₁ если они являются соседями.

Как будет выглядеть N, если улица является тупи­ком?

6. Вернемся к множеству S клеток шахматной доски. Отношение К связывает клетки, которые определяются ходом коня (т. е. если конь может перейти с х на у за один шаг). Определить К при помощи символов.

7. Пусть G — отношение на S такое, что 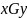тогда и только тогда, когда х есть начальная позиция (белой) пешки, а есть клетка, где первый ход игры заканчива­ется. Описать G, (G) и (G).