
- •Предисловие
- •Введение
- •Глава 1. Множества
- •§ 1. Множества н их спецификация
- •§ 2. Простейшие операции над множествами
- •X ∉ ø при любом х.
- •§ 3. Диаграммы Венна
- •§ 4. Подмножества и доказательства
- •§ 5. Произведения множеств
- •Глава 2. Отношения
- •§ 1. Основные понятия
- •§ 2. Графические представления
- •§ 3. Свойства отношений
- •§ 4. Разбиения и отношения эквивалентности
- •§ 5. Отношения порядка
- •§ 6. Отношения на базах данных и структурах данных
- •§ 7. Составные отношения
- •§ 8. Замыкание отношений
- •Глава 3. Функции
- •§ 1. Функции и отображения
- •§ 2. Обратные функции и отображения
- •§ 3. Мощность множеств и счетность
- •§ 4. Некоторые специальные классы функций
- •§ 5. Аналитические свойства вещественных функций
- •§ 6. Операции
- •Глава 4. Основные понятия арифметики
- •§ 1. «Малая» конечная арифметика
- •§ 2. «Большая» конечная арифметика
- •§ 3. Двоичная арифметика
- •§ 4. Логическая арифметика
- •Глава 5. Алгебраические структуры
- •§ 1. Алгебраические структуры и подструктуры
- •§ 2. Простейшие операционные структуры
- •§ 3. Кольца и поля
- •§ 4. Линейная алгебра
- •4.1. Векторные пространства о линейные преобразования.
- •§ 5. Решетка и булевы алгебры
- •§ 6. Замкнутые полукольца
- •Глава 6. Матрицы
- •§ 1. Матрицы и бинарные отношения на конечных множествах
- •§ 2. Матрицы над другими алгебраическими структурами
- •§ 3. Матрицы и векторные пространства
- •Глава 7. Теория графов
- •§ 1. Вводные понятия
- •§ 2. Маршруты, циклы и связанность.
- •§ 3. Планарные графы
- •3.1. Теоремы Эйлера и Куратовского.
- •3.2. Раскраска карт и графов.
- •§ 4. Структуры данных для представления графа
- •§ 5. Обход графа
- •5.2. Обход графа по глубине.
- •5.4. Остовные леса обходов по глубине и ширине.
- •§ 6. Ориентированные графы
- •6.2. Маршруты и связность в орграфах.
- •Глава 8. Языки и грамматики
- •§ 1. Основные понятия
- •§ 2. Грамматики с фразовой структурой
- •2.1. Основные определения.
- •§ 3. Контекстно-свободные языки
- •§ 4. Понятия грамматического разбора и грамматических модификаций
- •§ 5. Грамматики операторного предшествования
- •Глава 9. Конечные автоматы
- •§ 1. Общие понятия
- •§ 2. Конечные автоматы
- •§ 3. Регулярная алгебра
- •Глава 10.Компьютерная геометрия
- •§ 1. Системы координат для подмножеств r3
- •§ 2. Преобразования
- •§ 3. Кривые и поверхности
Глава 3. Функции
Понятие функции может быть уже известным читателю, однако в этой главе мы будем рассматривать функции как множество бинарных отношений. Собственно, будет дано определение функции и близкого к ней понятия отображения и изучены различные свойства, которыми они обладают. Затем функции будут использованы для того, чтобы формализовать процесс вычислений и дать определение мощности множества. В заключение будут рассмотрены конкретные функции, представляющие особый интерес, и функции, которые удобно определить с помощью операторов.
§ 1. Функции и отображения
Определение. Бинарное отношение ρ между множествами А и В является функцией, если из aρb и а ρ c следует, что b= с; поэтому для любого xϵA существует одно yϵB такое, что хρу. Можно дать определение функции следующим образом:
ρ(х)=ø или ρ(х)={y}. //
Следует помнить, что если ρ(х) существует (т. е. ρ(х)≠ø), то этот элемент единствен. В случае, когда р(х)≠ø, обычно опускают скобки при обозначении множества и записывают
y=ρ(x)
Функции обычно обозначают строчными латинскими буквами f, g,h, ... или в специальных случаях особыми сочетаниями, например sin, log, Fn, ... Если f—функция между множествами А и В, то этот факт может быть записан как f: A→. В. В дальнейшем, если хϵА и хfу, мы будем обозначать это соотношение следующим образом:
f: х→у.
Это обозначение часто используют для того, чтобы описать правило, определяющее функцию (если оно существует).
Пример 1.1. Функция f: А→А, где А = {-1, 0, 1}, определяется соотношением f: x → x3. //
Даже когда f не является отображением (см. ниже), мы часто будем использовать фразы типа «f отображает х в х3». Понятия области определения и области значений в данном случае содержательны, поскольку функция является отношением, однако следует заметить, что обратная функция может не существовать.
Пример 1.2. На множестве {-1, 0, 1} отношение f: х → х2 является функцией, но обратной функции не существует, поскольку f-1(1)={-1,1}. //
Определение. Функция f: А → В является отображением, если ее область определения совпадает с А, т. е. 𝕯1=A. Функции, не являющиеся отображениями, называют частичными. Отображение на множество называют трансформацией (преобразованием).
Замечание. Часто терминология отличается от принятой в этой книге, особенно в американских книгах. Термины «функция» и «отображение» иногда используют как синонимы, а отображение в том смысле, как мы его определили, называют полной функцией.
Конечно, каждая функция может рассматриваться как отображение на своей области определения; иногда это полезно, когда строятся сложные функции. Как мы увидим в последующих параграфах, исследовать свойства функций легче в тех случаях, если на функцию наложить некоторые условия.
Функция f: А→R называется функцией, принимающей действительные значения, а функция, область определения которой совпадает с R, называется вещественной.
Рассмотрим ограничения, которые помогут нам понять, что происходит с отдельными элементами в результате применения к ним функций. Будем заниматься классификацией функций, определенных на множествах, и предполагать, что мы имеем мало информации об этих множествах. Далее будут рассмотрены функции на множествах, где определены такие операции, как сложение.
Определение. Функция f: А→В называется сюръективной (на), если R1 = В. Это означает, что для данного b ϵ В имеем f-1(b)≠ø. Функция f: А→ В является инъективной, если из а1, a2ϵA и f (a1)=f(a2) следует, что a1=a2. //
Итак, если f: А→В и f сюръективна, то для любого bϵB имеем f -1(b)ϵR(A)\ø. Это может быть проинтерпретировано следующим образом: каждая точка из В является «острым концом» по крайней мере одной f-стрелы, выходящей из А. Проиллюстрировать эту ситуацию достаточно трудно (исключая тривиальные случаи).
С другой стороны, наглядную характеристику инъек-тивности легко дать в виде ограничения или запрета.
 Функция
f
не
инъективна
в случае, изображенном на рис. 3.1, a.
Функция
f
не
инъективна
в случае, изображенном на рис. 3.1, a.
Для сравнения на рис. 3.1, b изображено зеркальное отражение, которое отличает функцию от бинарного отношения.
Если
f:
А
→ В
инъективна
и aϵ𝕯1,
то a
= f
-1(f
(а)). Далее, если b
ϵ
R1,
т.
е.
 и в данном случае f
-1
—
функция, то b=
f(f
-1(b)).
и в данном случае f
-1
—
функция, то b=
f(f
-1(b)).
Следовательно, если мы определим функцию Ix: X→X как тождественное отображение на X, т. е. Ix: x→x для всех xϵx, тогда, если f инъективна, то
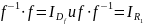
Используя
функцию f
из примера 1.2, мы видим, что
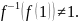 Это
означает, что первое из этих тождеств
в общем случае неверно, однако, как мы
увидим в § 2, вычисления становятся
гораздо легче в случаях, когда оба
тождества имеют место. Прежде чем
продолжить изложение, обсудим
терминологию, объединяющую введенные
выше свойства. Функция f
биективна,
если
она сюръективна и инъективна. Биективное
отображение называют биекцией.
Следовательно,
используя биекцию f
между А
и
В,
можно
брать элементы из А
и
переходить в В
посредством
f,
осуществляя некоторые вычисления.
Переход назад к А
осуществляется
посредством
Это
означает, что первое из этих тождеств
в общем случае неверно, однако, как мы
увидим в § 2, вычисления становятся
гораздо легче в случаях, когда оба
тождества имеют место. Прежде чем
продолжить изложение, обсудим
терминологию, объединяющую введенные
выше свойства. Функция f
биективна,
если
она сюръективна и инъективна. Биективное
отображение называют биекцией.
Следовательно,
используя биекцию f
между А
и
В,
можно
брать элементы из А
и
переходить в В
посредством
f,
осуществляя некоторые вычисления.
Переход назад к А
осуществляется
посредством
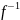 .
.
Термины инъекции и сюръекции также применяются (для описания инъективного и сюръективного отображений), однако мы редко будем их использовать.
Упражнение 3.1.
Какие из указанных ниже отношений на множестве {-10, -9, …, 0, 1, …, 9, 10} являются функциями? Дать противоречащие примеры в случаях, когда отношение не является функцией. (В 3.1, 1г) отношение порядка ≤ является отношением, индуцированным Z. В 3.1, 1а)—к) |x| определяется следующим образом: |х| = х, если х ≥ 0, и | х| = —х, если х < 0.)
a) p1 = {(x, у): х = у2};
б ) р2 = {(х, у): х2 = у}; в) р3 = {(х, у): х= -у};
г) p4 = {(x, y): х≤у};
д) р5 = {(х, у): х* у = 6};
е) р6 = { (х , у): х3 = у};
ж) р7 = {(х,у): х = у3};
з) р8 = { (х, у): х=|у|};
и) р9 = {(х, у): |х| = |у|};
к) p10 = {(x, у): у * |у| = х * | х|}.
Построить функцию f: А → А, где А = {0, 1}, не имеющую обратной.
Какие из следующих функций являются отображениями:
а) f
на R
определяется следующим образом:
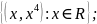
б) f
на R
определяется следующим образом:
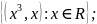
в) f
на R
определяется следующим образом:
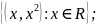
г) f
на R,

д) f
на R,
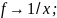
е) f
на Q,
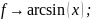
ж) f:
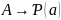 определяется следующим образом:
определяется следующим образом:
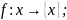
в)
f:
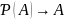 определяется следующим образом:
определяется следующим образом:
 ,
где a
—
фиксированный элемент из A?
,
где a
—
фиксированный элемент из A?
Пусть f:. А → В и g: В→С— отношения. Что является областью определения g∙f:
а) когда f и g — функции;
б) когда f — функция, g — отображение;
в) когда f — отображение, a g — функция;
г) когда fиg — отображения?
5. Доказать, что если функция f инъективна, то существует f-1.
Если функция f сюръективна, следует ли отсюда, что f-1 — отображение?
Построить пример, показывающий, что функция на A={-1,0,1}, определенная как f: x→x2, такова, что
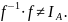
Пусть f: А → В и g: В → С — функции. Доказать, что:
а) если
fug
инъективны,
то
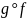 инъективна;
инъективна;
б) если f и g сюръективны, то также сюръек- тивна.
Пусть f: А
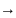 В
и
g:
В →
С
—
функции и g
сюръективна.
Достаточно ли этого, чтобы обеспечить
сюръек-тивность g°f?
В
и
g:
В →
С
—
функции и g
сюръективна.
Достаточно ли этого, чтобы обеспечить
сюръек-тивность g°f?
