
- •Предисловие
- •Введение
- •Глава 1. Множества
- •§ 1. Множества н их спецификация
- •§ 2. Простейшие операции над множествами
- •X ∉ ø при любом х.
- •§ 3. Диаграммы Венна
- •§ 4. Подмножества и доказательства
- •§ 5. Произведения множеств
- •Глава 2. Отношения
- •§ 1. Основные понятия
- •§ 2. Графические представления
- •§ 3. Свойства отношений
- •§ 4. Разбиения и отношения эквивалентности
- •§ 5. Отношения порядка
- •§ 6. Отношения на базах данных и структурах данных
- •§ 7. Составные отношения
- •§ 8. Замыкание отношений
- •Глава 3. Функции
- •§ 1. Функции и отображения
- •§ 2. Обратные функции и отображения
- •§ 3. Мощность множеств и счетность
- •§ 4. Некоторые специальные классы функций
- •§ 5. Аналитические свойства вещественных функций
- •§ 6. Операции
- •Глава 4. Основные понятия арифметики
- •§ 1. «Малая» конечная арифметика
- •§ 2. «Большая» конечная арифметика
- •§ 3. Двоичная арифметика
- •§ 4. Логическая арифметика
- •Глава 5. Алгебраические структуры
- •§ 1. Алгебраические структуры и подструктуры
- •§ 2. Простейшие операционные структуры
- •§ 3. Кольца и поля
- •§ 4. Линейная алгебра
- •4.1. Векторные пространства о линейные преобразования.
- •§ 5. Решетка и булевы алгебры
- •§ 6. Замкнутые полукольца
- •Глава 6. Матрицы
- •§ 1. Матрицы и бинарные отношения на конечных множествах
- •§ 2. Матрицы над другими алгебраическими структурами
- •§ 3. Матрицы и векторные пространства
- •Глава 7. Теория графов
- •§ 1. Вводные понятия
- •§ 2. Маршруты, циклы и связанность.
- •§ 3. Планарные графы
- •3.1. Теоремы Эйлера и Куратовского.
- •3.2. Раскраска карт и графов.
- •§ 4. Структуры данных для представления графа
- •§ 5. Обход графа
- •5.2. Обход графа по глубине.
- •5.4. Остовные леса обходов по глубине и ширине.
- •§ 6. Ориентированные графы
- •6.2. Маршруты и связность в орграфах.
- •Глава 8. Языки и грамматики
- •§ 1. Основные понятия
- •§ 2. Грамматики с фразовой структурой
- •2.1. Основные определения.
- •§ 3. Контекстно-свободные языки
- •§ 4. Понятия грамматического разбора и грамматических модификаций
- •§ 5. Грамматики операторного предшествования
- •Глава 9. Конечные автоматы
- •§ 1. Общие понятия
- •§ 2. Конечные автоматы
- •§ 3. Регулярная алгебра
- •Глава 10.Компьютерная геометрия
- •§ 1. Системы координат для подмножеств r3
- •§ 2. Преобразования
- •§ 3. Кривые и поверхности
§ 2. Грамматики с фразовой структурой
2.1. Основные определения.
О п р е д е л е н и е. Грамматикой с фразовой структурой (ГФС) G называется алгебраическая структура, состоящая из упорядоченной четверки (N, Т, P, S), где:
а) N и T — непустые конечные алфавиты нетерминальных и терминальных символов соответственно таких, что N T = ;
б) P
— конечное
множество продукций,
P
 ,
где V
= N
T
называется словарем
G;
,
где V
= N
T
называется словарем
G;
в) S N называется начальным символом или источником. //
Предполагая, что символ
не содержится в V,
соотношение
(
,
)
P
обычно записывают
в виде
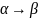 .
.
Понятие продукции, которую также называют правилом преобразования, должно давать возможность заменять одну строку символов другой. Терминальные символы обычно рассматриваются как неизменяемые символы. Поэтому, возможно, определение продукции в ГФС является чрезмерно общим. На практике соответствующие ограничения будут вводиться так, чтобы не нарушать постоянства терминальных символов, однако сейчас этого определения достаточно.
В качестве первого шага рассмотрим рис. 8.1 и попытаемся понять, как он связан со следующими примерами.
Пример 2.1. Предложение на английском языке, приведенное ранее в качестве иллюстрации, может быть определено в грамматике G = (N, Т, P, S), где N = {<предложение>, <подлежащее>, <артикль>, <существительное>, <сказуемое>, <дополнение>}; T = {the, dog, bit, me}; P = {(<предложение>, <существительное>, <сказуемое>, <дополнение>), (<существительное>, <артикль>, <подлежащее>), (<артикль> the), (<подлежащее> dog), (<сказуемое> bit), (<дополнение> me)}; S = <предложение>.
Эта частная система порождает только одно предложение «the dog bit те» и, следовательно, может быть заменена на
N = {<предложение>),
Р = {(<предложение> the dog bit me)}
или даже на
L = {the dog bit me}.
Однако если мы в данном случае захотим расширить язык, чтобы включить в него все предложения, начинающиеся со слов, скажем, «the lion», «the rat», «the tiger», со сказуемыми «ate» и «attacked» и дополнениями «you» и «Napoleon» (тогда L будет иметь более 35 элементов), то это может быть сделано добавлением только семи дополнительных элементов к каждому из множеств T и Р. В этом примере размер языка составляет 4 3 3, в то время как размер множества P примерно равен 4 + 3 + 3. Еще большее значение имеет тот факт, что мы можем включить все предложения вида «the dog bit (the son of)n Napoleon» (их бесконечное множество), добавляя к T и P незначительное число элементов. II
Перед тем как описать механизм порождения предложений, мы должны упомянуть нотацию, введенную Бэкусом (нормальная форма Бэкуса или форма Бэкуса-Наура, БНФ). Она особенно полезна, когда мы хотим использовать элементы из N, которые можно спутать с элементами из T такими, как (предложение) и «предложение». Эта нотация использует четыре символа:
::= (мета-присвоить), < (мета-открыть),
> (мета-закрыть), | (мета-или).
Понятия «мета-открыть» и «мета-закрыть» используются для того, чтобы выделять строки в качестве элементов N, «мета-присвоить» заменяет символ , и если ( , ) Р, ( , ) P, то это может быть записано в виде ::= | , что читается как « есть или ».
БНФ впервые использовалась для определения синтаксиса Алгол-60. В случае если у читателя имеются какие-либо сомнения в том, что БНФ способна определить что-нибудь серьезное, рекомендуем прочитать сообщение про Алгол-60. В работах по формальным языкам обычно избегают длинных строк в N и, следовательно, нотация Бэкуса не используется, за исключением символа мета-или. Обычно прописные буквы используют для обозначения элементов N, а строчные — для элементов Т.
Пример 2.2. Рассмотрим G=(N, Т, P, S), где
N = {S, Т}, Т - {а, b, с, d},
P = {S aTd, T bT | b | cT | c}.
Заметим, что двойное использование T в этом примере не вызывает никаких затруднений.
Грамматика будет порождать все строки a{b, c}+d, однако мы все еще не показали, как этого можно достичь. Будем использовать продукции следующим образом.
Пусть
,
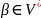 ;
тогда
прямо
выводится из
,
если
=
;
тогда
прямо
выводится из
,
если
=
 и
=
и
=
 ,
где
,
,
,
где
,
,
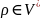 ,
,
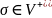 и
и
 .
Этот факт будем
записывать в виде
.
Этот факт будем
записывать в виде
 ;
он может неформально рассматриваться
как преобразования строки
в строку
замещением подстроки
в
на
.
(Заметим, что не обязательно заменять
конкретное вхождение
в
или использовать конкретную продукцию
с левой частью
.
Возможны любые
вариации.)
;
он может неформально рассматриваться
как преобразования строки
в строку
замещением подстроки
в
на
.
(Заметим, что не обязательно заменять
конкретное вхождение
в
или использовать конкретную продукцию
с левой частью
.
Возможны любые
вариации.)
Пусть теперь
и
— слова
над V
и существует
конечная последовательность
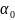 ,
,
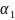 ,
…,
,
…,
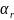 ,
где
=
,
=
и
,
где
=
,
=
и
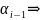 ai
(i
= l,
…, r).
Тогда будем говорить, что
порождает
(записывается
)
и что вывод
из
реализуется следующим образом:
ai
(i
= l,
…, r).
Тогда будем говорить, что
порождает
(записывается
)
и что вывод
из
реализуется следующим образом:
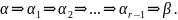 Аналогично
,
если вывод использует непустую
последовательность прямых выводов.
Если
V*
такое, что S
Аналогично
,
если вывод использует непустую
последовательность прямых выводов.
Если
V*
такое, что S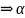 ,
то
называют сентенциальной
формой.
Более того, если
T*
и
,
то
называют сентенциальной
формой.
Более того, если
T*
и
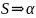 ,
то
является предложением,
порожденным G.
Таким образом,
язык L(G),
порожденный G,
есть {
:
Т*
и S*
}.
Там, где G
подразумевается,
можно определить L(X)
={
:
Т*,
X
N
и X
}.
Поскольку, применяя продукции к
сентенциальным формам, можно действовать
достаточно произвольно, то возможно
существование нескольких допустимых
выводных последовательностей для
данного предложения в L(G),
где G
— конкретная
грамматика. Среди этих последовательностей
мы выбираем ту, которая на каждом этапе
оперирует с самой левой из возможных
подстрок, в которой элементы заменяются
на элементы из Р.
Такая последовательность
называется (левой) канонической
выводной последовательностью для
предложения.
,
то
является предложением,
порожденным G.
Таким образом,
язык L(G),
порожденный G,
есть {
:
Т*
и S*
}.
Там, где G
подразумевается,
можно определить L(X)
={
:
Т*,
X
N
и X
}.
Поскольку, применяя продукции к
сентенциальным формам, можно действовать
достаточно произвольно, то возможно
существование нескольких допустимых
выводных последовательностей для
данного предложения в L(G),
где G
— конкретная
грамматика. Среди этих последовательностей
мы выбираем ту, которая на каждом этапе
оперирует с самой левой из возможных
подстрок, в которой элементы заменяются
на элементы из Р.
Такая последовательность
называется (левой) канонической
выводной последовательностью для
предложения.
Пример 2.3. Пусть
G=({B}, {( , )}, Р, B),
где
Р = {В (В)|ВВ|( )}.
Тогда предложение ( ) (( ) ( )) может быть выведено многими способами.
Приведем пять из них:
1) B BB
( )B
( )(B)
( )(BB)
( )(( )B)
( )(( )( ));
3) B BB
B(B)
( )(B)
( )(BB)
( )(( )B)
( )(( )( ));
5) B BB
B(B)
B(BB)
B(( )B)
( )(( )B)
( )(( )( )).
2) B BB
( )B
( )(B)
( )(BB)
( )(B( ))
( )(( )( ));
4) B BB
B(B)
( )(B)
( )(BB)
( )(B( ))
( )(( )( ));
Первый из этих выводов является каноническим.
2.2. Иерархия Хомского. Обсуждавшаяся до сих пор система — сильное описательное средство, однако при создавшемся положении вещей она является слишком общей. Тем не менее, если наложить ограничения, мы получим более интересный, хотя все еще достаточно мощный математический объект. Начальные ограничения, которые мы будем накладывать па структуру грамматики, определяют элементы Р.
Определение
(иерархия Хомского). Пусть G=(N,
Т,
Р,
S)
является ГФС,
описанной в п. 2.1. Такую грамматику
называют грамматикой
Хомского типа 0.
Если все элементы P
получаются из
формы
,
где
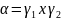 ,
a
,
a
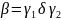 ,
,
,
,
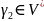 ,
x
N,
,
x
N,
 ,
то говорят,
что G
является
контекстно-зависимой грамматикой, или
грамматикой
Хомского типа 1
(КЗГ). (В
этом определении строки
,и
,
то говорят,
что G
является
контекстно-зависимой грамматикой, или
грамматикой
Хомского типа 1
(КЗГ). (В
этом определении строки
,и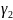 могут
рассматриваться как контекст, в
котором х
может заменяться
посредством
.)
Другим (альтернативным) ограничением
для грамматики Хомского типа 1
является то, что в каждой продукции
и
должны быть такими, что 1 ≤ |
|
≤ |β
|. (Эквивалентность этих двух
определений неочевидна и доказывается
ниже.) Если подстановки могут быть
выполнены без
рассмотрения контекстов, тогда мы можем
заменить «контексты»
и
пустой строкой
Λ и
получить
более слабое ограничение:
если x
→
δ ∈ P,
то x
∈
N
и δ
∈
могут
рассматриваться как контекст, в
котором х
может заменяться
посредством
.)
Другим (альтернативным) ограничением
для грамматики Хомского типа 1
является то, что в каждой продукции
и
должны быть такими, что 1 ≤ |
|
≤ |β
|. (Эквивалентность этих двух
определений неочевидна и доказывается
ниже.) Если подстановки могут быть
выполнены без
рассмотрения контекстов, тогда мы можем
заменить «контексты»
и
пустой строкой
Λ и
получить
более слабое ограничение:
если x
→
δ ∈ P,
то x
∈
N
и δ
∈
 .
Этому ограничению удовлетворяют
грамматики
Хомского типа 2.
Наконец, если P
состоит только
из продукций вида х→𝛿,
где и δ
∈ T
∪
TN
(так, что правая
часть является или единичным терминалом,
или единичным терминалом, за которым
следует единичный нетерминал), то
говорят, что G
является грамматикой
Хомского типа 3.
//
.
Этому ограничению удовлетворяют
грамматики
Хомского типа 2.
Наконец, если P
состоит только
из продукций вида х→𝛿,
где и δ
∈ T
∪
TN
(так, что правая
часть является или единичным терминалом,
или единичным терминалом, за которым
следует единичный нетерминал), то
говорят, что G
является грамматикой
Хомского типа 3.
//
Часто бывает полезно использовать более общие формы внутри множества продукций, хотя формально это и не разрешается. Хотелось бы быть в состоянии включить пустую строку Λ в качестве правой части любой продукции. Однако, как увидим позднее, это вызывает трудности. Такие Λ - продукции крайне необходимы с общей точки зрения, если только Λ ∈ L. В этом случае мы можем добавить S → Λ к P при условии, что S не встречается в правой части любой продукции. Однако в некоторых случаях необходимо разрешать также и более общие Л-продукции. Чтобы различать грамматики Хомского и те грамматики, в которых разрешаются Λ- продукции, введем расширенные версии грамматик Хомского типа 2 и 3 — контекстно-свободные и регулярные грамматики соответственно. Языки, порожденные каким-либо из этих типов грамматик, имеют аналогичные названия. Так, структурная грамматика порождает структурный язык, структурная грамматика Хомского типа 1 — язык Хомского типа 1, контекстно-свободная грамматика — контекстно-свободный язык, а регулярная грамматика порождает регулярный язык (или регулярное множество). Большинство примеров этой главы будет касаться контекстно-свободных языков, а в гл. 9 мы сконцентрируем внимание на регулярных языках. Однако большинство практических языков являются некоторыми расширениями контекстно-зависимых языков. Чтобы указать на ограничения контекстно-свободной грамматики, рассмотрим следующий важный пример.
Пример 2.4. {xnynzn: п ∈ N} является контекстно-зависимым языком. Предположим, что G = (N, Т, P, S), где
N = {S, X, Y, Z}, T = {x, y, z}, Р = {Р1, ..., Р7),
P1 = S → xSYZ, P2 = S → xYZ,
Р3 = xY → ху, P4 = yY → yy, Р5 = yZ → yz,
P6 = ZY → YZ, P7 = zZ → zz.
Вначале заметим, что для любого n ∈ N мы можем получить
∗
S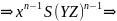 (P1)
(P1)
∗
 (P2)
(P2)
∗
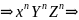 (P6)
(P6)
∗
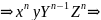 (P3)
(P3)
∗
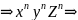 (P4)
(P4)
∗
 (P5)
(P5)
∗
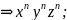 (P7)
(P7)
поэтому
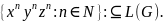
Теперь мы должны показать, что никакие другие строки не могут быть порождены G. Хотя возможны некоторые изменения в порядке применения правил (P1), (Р2) и (Р6), любое предложение должно выводиться посредством сентенциальной формы такой, как xnYZ𝛼, где 𝛼 состоит из п - 1 символов Y и Z. Для того чтобы получить строку над T, мы должны в конце концов использовать правила (Р4), (Р5) и (Р7), однако (Р7) может преобразовать Z в z только в контексте zZ, а (Р5) осуществляет такую же замену в контексте yZ. Аналогично для замены Y на у при помощи правил (Р4) и (Р3) требуются контексты yY и xY соответственно. На этой стадии подстрока хп состоит только из терминалов, поэтому на следующем шаге строка должна иметь вид xnyZ𝛼 и получаться при помощи (P3). Однако мы знаем, что правильное предложение должно порождаться преобразованием из Z𝛼 в Yn-1Zn посредством (Р6). Действительно, только таким образом можно успешно получить строку.
Предположим, что мы имеем промежуточную подстроку вида yYmZpY𝛽, где 𝛽 состоит из оставшихся элементов Y и Z. Иэ рассуждений, аналогичных приведенным выше, следует, что для получения подстроки ym+1ZpY𝛽 нужно т раз применить (Р4). Однако, если сейчас мы используем (Р5) для получения ym+1zZp-1Y𝛽, то никаким правилом нельзя заменить элемент Y на у (или любой другой терминал). Единственный способ выйти из этого положения — это p раз применить (P6), чтобы переместить Y влево и, следовательно, получить xnynzn. //
Это пример контекстно-зависимого языка, который, как будет показано, не является контекстно-свободным. Аналогично существуют контекстно-свободные языки, которые не являются регулярными (см. гл. 9). Вернемся теперь к доказательству эквивалентности альтернативных определений контекстно-зависимых грамматик.
Определение. Грамматики G1 и G2 эквивалентны, если
L(G1) = L(G2). //
Предложение. L является контекстно-зависимым языком тогда и только тогда, когда он может быть порожден грамматикой, у которой продукции 𝜎→𝜇 удовлетворяют условию 1 ≤ |σ| ≤ |μ|.
Доказательство. Если L —- контекстно-зависимый язык, то существует грамматика G с продукциями вида 𝛼Аβ → 𝛼𝛾β, где А ∈ N, 𝛾 ∈ и 𝛼, β ∈ V* такие, что L = L(G). Однако
|𝛼Аβ| = |𝛼| + |A| + |β| = |𝛼| + 1 + |β| ≥ 1,
|𝛼𝛾β| = |𝛼| + |𝛾| + |β| ≥ |𝛼| + 1 + |β| = |𝛼Аβ|.
Следовательно, 1 ≤ |𝛼Аβ| ≤ |𝛼𝛾β|, что и требовалось доказать.
Пусть G = (N, Т, Р, S) — грамматика, у которой продукции σ → μ удовлетворяют соотношению 1 ≤ |σ| ≤ |μ|. Мы должны создать грамматику G', эквивалентную G, с продукциями вида 𝛼Аβ → 𝛼𝛾β.
Продукции из G имеют вид
A→ 𝛾1… 𝛾p или же
𝛼1… 𝛼n → β1…βq, где n ≤ q и A ∈ N, αi, βi, γi ∈ V.
Во всех продукциях заменим каждый встречающийся элемент ai ∈ T новым нетерминальным элементом Ai и включим продукции Ai → аi в G'. Продукции типа 1) теперь имеют правильную форму и включены в G'. Однако продукции типа 2) необходимо модифицировать. Сейчас они имеют вид
W1...Wn→Y1...Yq, n ≤ q,
где Wi и Yi являются нетерминальными символами новой грамматики. Для каждой такой продукции введем новые элементы Ŷ1, …, Ŷq, не являющиеся терминалами, и п + q новых продукций: п продукций
W1 ... Wn→Ŷ1W2...Wn,
Ŷ1W2, ... Wn→Ŷ1Ŷ2W3...Wn, . . . . . . . . . . . .
Ŷ1 ... Ŷn-2Wn-1Wn → Ŷ1 ... Ŷn-2Ŷn-1Wn,
Ŷ1 ... Ŷn-2Ŷn-1Wn → Ŷ1 ... Ŷn-2Ŷn-1ŶnŶn+1…Ŷq
и q продукций
Ŷ1Ŷ2…Ŷq→Y1Ŷ2 …Ŷq,
Y1Ŷ2…Ŷq→Y1Y2Ŷ3 …Ŷq,
. . . . . . . . . .
Y1Y2…Y q-1Ŷq→Y1Y2…Yq-1Yq,
Все эти продукции имеют вид 𝛼Аβ → 𝛼𝛾β.
Новые нетерминалы Ŷ1, …, Ŷq вынуждают применять эти продукции в написанном порядке так, чтобы никакие из предложений, не входящих в исходный язык, не могли быть созданы. //
В заключение этого параграфа обсудим понятие неоднозначности. Классическим примером неоднозначного предложения является предложение
«They are flying planes».
Мы имеем две интерпретации этого предложения, зависящие от того, рассматриваем мы «аrе flying» как сказуемое или же «flying planes» как дополнение. Это приводит нас непосредственно к точному определению неоднозначности. Язык называется неоднозначным, если он содержит неоднозначное предложение. Предложение является синтаксически неоднозначным, если оно имеет более одного канонического вывода, и семантически неоднозначным, если для заданного канонического вывода оно имеет более одной интерпретации. (Выводы относятся не непосредственно к языку, а к грамматике, порождающей его. Следовательно, мы должны ссылаться на неоднозначную грамматику; однако существуют существенно неоднозначные языки, которые могут порождаться только неоднозначными грамматиками.) Для более подробного изучения семантических неоднозначностей рекомендуем обратиться к специальной литературе о языках программирования, а сейчас проиллюстрируем синтаксические неоднозначности двумя примерами.
Пример 2.5.
1. Пусть G = ({E}, {1, -}, {Е → E – E |1}, Е). Тогда
а) E ⇒ E – Е ⇒
⇒ 1 – Е ⇒
⇒ 1 – Е – Е ⇒
⇒ 1 – 1 – Е ⇒
⇒ 1 – 1 – 1;
а) E ⇒ E – Е ⇒
⇒ Е – E – Е ⇒
⇒ 1 – Е – Е ⇒
⇒ 1 – 1 – Е ⇒
⇒ 1 – 1 – 1.
И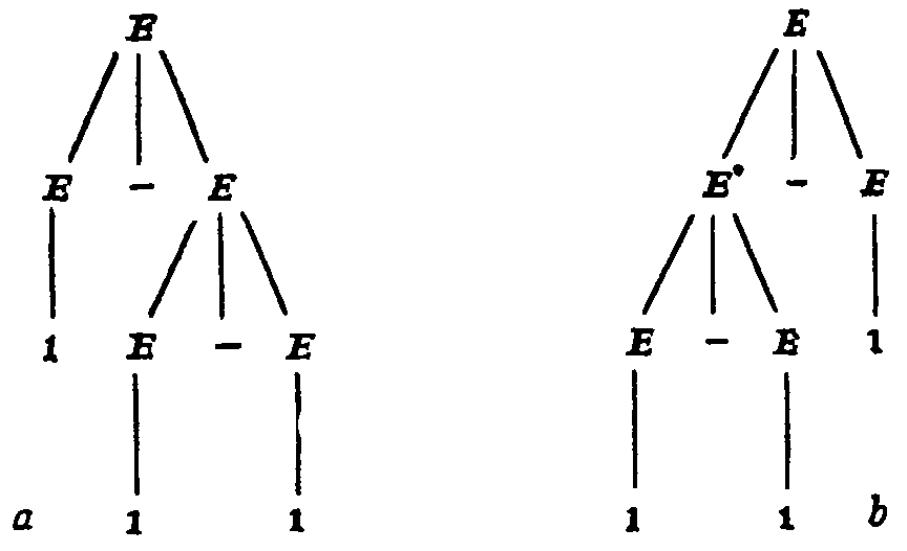 з
этих последовательностей следует, что
два указанных вывода являются различными,
и, следовательно, хотелось бы придать
им различные значения. В примере а)
з
этих последовательностей следует, что
два указанных вывода являются различными,
и, следовательно, хотелось бы придать
им различные значения. В примере а)
Рис. 8.2
второй знак «минус», вычисляемый вначале, дает 1; в примере б) первый знак «минус», выполняемый первым, дает -1. (Диаграммы на рис. 8.2 иллюстрируют различные структуры.
2. Рассмотрим хорошо известный пример из первой спецификации языка Алгол-60. Сужая грамматику до относящегося к делу подъязыка, будем иметь продукции
S → if В then S else S | if В then S | U,
где S — утверждение, В — булево выражение, U — безусловное утверждение. Теперь рассмотрим выражение
if B1 then if B2 then U1 else U2.
Мы не знаем, принадлежит ли else U2 к if В1 или к if В2. Формально мы можем вывести это предложение, рассматривая B и U как терминалы, следующим образом (рис. 8.3, a, b соответственно):
a) S ⇒ if В then S ⇒
⇒ if В then if В then S else S ⇒
⇒ if В then if В then U else S ⇒
⇒ if B then if В then U else U;
б) S ⇒ if В then S else S ⇒
⇒ if B then if B then S else S ⇒
⇒ if В then if B then U else S ⇒
⇒ if В
then
if B
then U
else
U.
//
if В
then
if B
then U
else
U.
//
Рис. 8.3
У п р а ж н е н и е 2.2.
Выразить явно языки, определенные следующими грамматиками:
а) G = ({<число>, {0, 1, 2, …, 9}, Р, <число>), где Р = {<число> → 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9};
б) G = ({<P>, <L>, <D>, {0, 1, 2, …, 9}, Р, <Р>), где
Р = {<Р> → <L><D> | <L>,
<L> → 1 | 2 | 3 … 8 | 9, <D> → <L>, <D> → 0}.
Определить грамматику G' = (N', Т', Р', S'), эквивалентную
G =({A, B, C, S), {х, у, z}, Р, S),
где
Р = {S → АВ2С, АВ → BAz, zB → A2Bx, А → х,
В → у, C → z},
с продукциями вида 𝛼Qβ → 𝛼𝛾β для
Q ∈ N', 𝛾∈(N' ∪ T')+, 𝛼, β ∈ (N' ∪ T')*.
Определить класс Хомского грамматики, определенной следующим образом:
G = ({A, В, T, S), {x, y, z}, Р, S),
где
P = (S → хТВ | хВ, Т → хТА | хА,
В → yz, Ay → уA, Az → yzz}.
Используя свойство класса, к которому принадлежит G, установить, принадлежат или нет L(G) следующие строки:
x2yxz, x2y2z2, xyxz.
4. Определить последовательность разрезов представленного здесь производящего дерева, соответствующую самому правому выводу предложения х + x ∗ х.
О
 пределить
порядок в множестве продукций P
таким образом,
чтобы была возможность канонического
вывода, определяющего последовательность
целых чисел в N. Продемонстрировать
две такие последовательности для
предложения «aza»
в L(G1),
где G1
дано ниже. Вывести
также строку над N,
описывающую все выводы в языке L(G2),
т. е. показать,
что A
⇒
A
подразумевает
неоднозначность. Здесь
пределить
порядок в множестве продукций P
таким образом,
чтобы была возможность канонического
вывода, определяющего последовательность
целых чисел в N. Продемонстрировать
две такие последовательности для
предложения «aza»
в L(G1),
где G1
дано ниже. Вывести
также строку над N,
описывающую все выводы в языке L(G2),
т. е. показать,
что A
⇒
A
подразумевает
неоднозначность. Здесь
G1= (N,T,P,E), G2 = (N,T,P,A),
где N = {А, В, С, Е, R}, Т = {a, d, е, х, z} и
P = {А → В | Cd, В → Вх | еС | С,
C → A | xR,E → aE | Ea | R, R → z}.
Выяснить, являются ли следующие грамматики неоднозначными:
а) G = ({A, В, S}, {а, b, с}, Р, S), где P = {S → AB, А → а | ab, В → c | bc};
б) G = ({<целое без знака>, <число>}, D, P, <целое без знака>), где D = (0, 1, …, 9} и P= {<целое без знака> → <число>),
<число> → <число> <число>, <число> → 0 | 1 | 2…| 9}.
