
- •С.П. Кудаев
- •Учебно-методическое пособие по организации самостоятельной работы студентов офо и контрольные задания для студентов зфо по специальности 151001.65 «Технология машиностроения».
- •Введение
- •Список рекомендуемой литературы
- •430027, Г. Саранск, ул. Большевистская, 68
- •431440, Г. Рузаевка, ул. Трынова, 67а
С.П. Кудаев
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
ПРОЦЕССОВ В МАШИНОСТРОЕНИИ

минстерство образования и науки рф
Федеральное ГОСУДАРСТВЕННОЕ бюджетное ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«МОРДОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
имени Н.П. ОГАРЕВА»
РУЗАЕВСКИЙ ИНСТИТУТ МАШИНОСТРОЕНИЯ (ФИЛИАЛ)
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССОВ В МАШИНОСТРОЕНИИ
Учебно-методическое пособие по организации самостоятельной работы студентов офо и контрольные задания для студентов зфо по специальности 151001.65 «Технология машиностроения».
Саранск 2012 год.
УДК 517. 8
Математическое моделирование процессов в машиностроении: Учебно-методическое пособие по организации самостоятельной работы студентов и контрольные задания. С.П. Кудаев. Рузаевка: Типография «Рузаевский печатник», 2012. – 79 с.
Рецензенты:
кафедра общенаучных дисциплин Рузаевского института машиностроения (филиала) ФГБОУ ВПО «Мордовский государственный университет имени Н.П. Огарева» (заведующий кафедрой д.ф.-м.н., профессор Кузьмичев Н.Д.)
к.т.н., доцент Власкин В.В.
Учебно-методическое пособие содержит задания для организации самостоятельной работы студентов очной и заочной форм обучения, изучающих дисциплину «Математическое моделирование процессов в машиностроении». Приводятся методические указания по выполнению заданий и примеры выполнения.
Предназначены для студентов Рузаевского института машиностроения (филиала) ФГБОУ ВПО «Мордовский государственный университет имени Н.П. Огарева», обучающихся по специальности 151001 «Технология машиностроения».
Печатается по решению научно-методического совета Мордовского государственного университета имени Н.П. Огарева
Введение
Целью преподавания дисциплины «Математическое моделирование процессов в машиностроении» является ознакомление студентов с рядом разделов теории вероятностей и математической статистики, получение умений и навыков решения задач технологии машиностроения на основе математического моделирования.
В результате изучения дисциплины студенты должны получить представление о математических подходах к решению различных задач, возникающих при проектировании технологических процессов, эксплуатации технологического оборудования и оснастки, организации производственного процесса изготовления изделий.
В процессе изучения дисциплины самостоятельная работа организуется в виде выполнения индивидуальных заданий. Предусмотрено выполнение восьми заданий. Для студентов заочной формы обучения задания №1, №2, №3, №4 составляют содержание контрольной работы № 1, а задания №5, №6, №7, №8 – контрольной работы № 2.
Численные значения параметров задачи определяются шифром – двумя последними цифрами номера зачетной книжки. В приведенных заданиях i – предпоследняя, а j – последняя цифры номера зачетной книжки. Если i =0 или j =0, принять i =1 и j =1.
Задание выполняется в отдельной тетради, страницы которой нумеруются. На обложке указываются: название дисциплины, номер работы, фамилия и инициалы студента, шифр, специальность. На первой страницы записываются: номер контрольной работы, номера решаемых заданий.
Решение каждого задания следует обязательно начинать на развороте тетради (на четной страницы, начиная со второй). Сверху указывается номер задания и записывается текст задания. Решение заданий необходимо сопровождать краткими пояснениями (какие формулы применяются, откуда получаются те или иные результаты и т. п.) и подробно излагать весь ход расчетов. На каждой страницы следует оставлять поля для замечаний рецензента. При необходимости решения сопровождают графическими построениями. Чертеж должен быть аккуратным и наглядным.
На зачете необходимо представить зачтенные по данному разделу курса работы, в которых все отмеченные рецензентом погрешности должны быть исправлены.
Для каждого задания приводится пример решения. Цель примера – разъяснить ход решения, но не воспроизвести его полностью. Поэтому в ряде случаев промежуточные расчеты опускаются. Но при выполнении задания все преобразования и числовые расчеты должны быть обязательно последовательно проделаны с необходимыми пояснениями; в конце должны быть даны ответы.
Задание № 1.
Даны множества Е, А, В, С.
Е={0,
1,2, 3.4, 5, 6, 7, 8, 9},
А={![]() ,
4, 6, 8}, В={0, 1,
,
, 9}, С={5, 7,
,
4, 6, 8}, В={0, 1,
,
, 9}, С={5, 7,
![]() }.
}.
Определить следующие множества, образованные из множеств A, B и C:
1.
|
4.
|
2.
|
5.
|
3.
|
6.
|
Основные операции над множествами подробно описаны в главе 1 [1].
Пример выполнения задания № 1.
Даны множества Е, А, В, С. Е={1, 2, 3, 4, 5}, А={1, 5}, В={1, 2, 4}, С={2, 5}.
Определить следующие множества, образованные из множеств A, B и C:
-
1. .
2. .
3. .
4. .
5. \ \ .
6. .
РЕШЕНИЕ.
На основании определений основных операций над множествами, получаем [1]:
1.
={1,
5}![]() {3,
5}={5}.
{3,
5}={5}.
2.
={5}![]() {1,
2, 4}={1, 2, 4, 5}.
{1,
2, 4}={1, 2, 4, 5}.
3. ={1, 5} {2}={1, 2, 5}.
4. ={1, 2, 3, 4, 5} {1, 2, 5}={1, 2, 5}.
5. \ \ ={1} {1, 4}={1, 4}.
6.
=![]() \
\![]() ={1,
2, 4, 5}\{1}={2,
4, 5}.
={1,
2, 4, 5}\{1}={2,
4, 5}.
Задание № 2.
Решите следующие задачи, используя теоремы сложения и умножения вероятностей, формулы полной вероятности, Бейеса и Бернулли.
2.1. На складе находятся 50 деталей, изготовленных тремя бригадами. Из них 30 изготовлено первой бригадой, 1j – второй, остальные – третьей. Определить вероятность поступления на сборку детали, изготовленной второй или третьей бригадой.
2.2. Определить вероятность того, что партия в 100 изделий, среди которых j бракованных, будет принята при испытании, если условиями приема допускается не более 1 бракованного изделия из 50.
2.3. Фрезеруется деталь имеющая форму прямоугольного параллелепипеда. Деталь считается годной, если отклонение размера каждого из ребер от заданного чертежом не превышает 0,01. Вероятность отклонений, превышающих 0,01 составляет по длине Р1=0,0i, по ширине Р2=0,1j, по высоте Р3=0,1. Найти вероятность Р годности детали.
2.4. На сборку поступают шестерни с трех зубофрезерных автоматов. Первый дает 25%, второй 30 % и третий 45% шестерен, поступающих на сборку. Первый автомат допускает 0,i0 % брака шестерен, второй – 0,j0 %, третий – 0,30 %. Найти вероятность поступления на сборку бракованной шестерни и вероятность того, что оказавшаяся бракованной шестерня изготовлена первым автоматом.
2.5. Механическая обработка детали производилась одновременно тремя инструментами. В результате контроля деталь признана негодной. Определить вероятность того, что деталь была признана негодной в результате обработки первым, вторым или третьим инструментом, если вероятности брака для них соответственно равны 0,i0; 0,j0; 0,6.
Теоретический материал для данного задания подробно изложен в [1, 2, 3].
Пример выполнения задания № 2.
Решите следующие задачи, используя теоремы сложения и умножения вероятностей, формулы полной вероятности, Бейеса.
Задание 2.1. На складе находятся 50 деталей, изготовленных тремя бригадами. Из них 30 изготовлено первой бригадой, 12 – второй, остальные – третьей. Определить вероятность поступления на сборку детали, изготовленной второй или третьей бригадой.
РЕШЕНИЕ.
Вероятность
поступления детали, изготовленной
второй бригадой
![]() ,
а вероятность поступления детали,
изготовленной третьей бригадой,
,
а вероятность поступления детали,
изготовленной третьей бригадой,
![]() .
Так как появление на сборке одной детали
исключает появление другой в том же
испытании, то события несовместны и на
основании теоремы о сложении вероятностей
получаем:
.
Так как появление на сборке одной детали
исключает появление другой в том же
испытании, то события несовместны и на
основании теоремы о сложении вероятностей
получаем:
![]()
Этот
результат можно получить иным способом.
Событие, состоящее в поступлении на
сборку детали из второй или третьей
бригады, эквивалентно событию непоступления
на сборку детали из первой бригады.
Вероятность же поступления на сборку
детали из первой бригады равна
![]() ,
тогда вероятность противоположного
события и даст искомую вероятность
,
тогда вероятность противоположного
события и даст искомую вероятность
![]() :
:
![]() .
.
Задание 2.2. Определить вероятность того, что партия в 100 изделий, среди которых 5 бракованных, будет принята при испытании, если условиями приема допускается не более 1 бракованного изделия из 50.
РЕШЕНИЕ.
Из
100 деталей выбрать 50 можно
![]() способами. Из 95 годных изделий 49 годных
можно выбрать
способами. Из 95 годных изделий 49 годных
можно выбрать
![]() способами.
Из 5 бракованных изделий 1 бракованное
можно выбрать
способами.
Из 5 бракованных изделий 1 бракованное
можно выбрать
![]() способами. Пусть событие А состоит в
том, что при испытании не обнаружено ни
одного бракованного изделия. Вероятность
появления события А будет:
способами. Пусть событие А состоит в
том, что при испытании не обнаружено ни
одного бракованного изделия. Вероятность
появления события А будет:
 .
Пусть событие В заключается в том, что
при испытании обнаружена 49 годных
деталей и 1 бракованная. Число способов
отбора, приводящих к появлению события
В равно произведению
,
а вероятность появления события В будет
равна
.
Пусть событие В заключается в том, что
при испытании обнаружена 49 годных
деталей и 1 бракованная. Число способов
отбора, приводящих к появлению события
В равно произведению
,
а вероятность появления события В будет
равна
 .
Вероятность Р искомого события,
заключающегося в появлении либо события
А, либо события В определится в соответствии
с теоремой о сложении вероятностей как:
.
Вероятность Р искомого события,
заключающегося в появлении либо события
А, либо события В определится в соответствии
с теоремой о сложении вероятностей как:


Задание 2.3. Фрезеруется деталь имеющая форму прямоугольного параллелепипеда. Деталь считается годной, если отклонение размера каждого из ребер от заданного чертежом не превышает 0,01 мм. Вероятность отклонений, превышающих 0,01 мм составляет по длине Р1=0,02, по ширине Р2=0,14, по высоте Р3=0,1. Найти вероятность Р появления брака при обработки детали.
РЕШЕНИЕ.
Деталь
будет годной если выдержаны заданные
размеры (с отклонением 0,01 мм) по длине
(событие А), по ширине (событие В) и по
высоте (событие С), то есть события А, В
и С должны произойти одновременно, в
противном случае деталь окажется
бракованной. Эти три события могут
считаться независимыми, так как они
обусловлены различными причинами и
поэтому вероятность
![]() совместного
появления событий А, В, С определится
на основании теоремы умножения
вероятностей как:
совместного
появления событий А, В, С определится
на основании теоремы умножения
вероятностей как:
![]()
![]() .
.
Появление брака при обработки будет представлять собою событие, противоположное событию, состоящему в совместном появлении событий А, В, С. Поэтому искомая вероятность появления брака найдется как:
![]() .
.
Задание 2.4. На сборку поступают шестерни с трех зубофрезерных автоматов. Первый дает 25%, второй 30 % и третий 45% шестерен, поступающих на сборку. Первый автомат допускает 0,10 % брака, второй – 0,20 %, третий – 0,30 %. Найти вероятность поступления на сборку бракованной шестерни и вероятность того, что оказавшаяся бракованной шестерня изготовлена первым автоматом.
РЕШЕНИЕ.
Пусть событие А – поступление на сборку
бракованной шестерни. При этом возможны
следующие гипотезы:
![]() - шестерня изготовлена на первом,
- шестерня изготовлена на первом,
![]() - на втором,
- на втором,
![]() - на третьем автомате. По условию задачи
вероятности наступления событий
,
и
равны:
- на третьем автомате. По условию задачи
вероятности наступления событий
,
и
равны:
![]() ;
;
![]() ;
;
![]() .
Условные же вероятности появления
события А при наличии событий
,
и
соответственно равны
.
Условные же вероятности появления
события А при наличии событий
,
и
соответственно равны
![]() ;
;
![]() ;.
;.![]() Тогда, в соответствии с формулой полной
вероятности, вероятность
Тогда, в соответствии с формулой полной
вероятности, вероятность
![]() ,
поступления на сборку бракованной
шестерни определится как:
,
поступления на сборку бракованной
шестерни определится как:
![]()
![]() .
.
Вероятность
![]() гипотезы
после того как событие А имело место,
то есть вероятность того, что на сборку
поступила бракованная шестерня (событие
А) и она была изготовлена на первом
автомате (событие
),
определится по формуле Бейеса
гипотезы
после того как событие А имело место,
то есть вероятность того, что на сборку
поступила бракованная шестерня (событие
А) и она была изготовлена на первом
автомате (событие
),
определится по формуле Бейеса

![]() .
.
Задание 2.5.
Механическая обработка детали
производилась одновременно двумя
инструментами. В результате контроля
деталь признана негодной. Определить
вероятность того, что деталь была
признана негодной в результате обработки
первым или вторым инструментом, если
вероятности брака для них соответственно
равны
![]() ,
,
![]() .
.
РЕШЕНИЕ.
Возможны четыре гипотезы:
![]() - оба инструмента дает годные размеры,
- первый инструмент дает брак, второй -
годный размер,
- первый инструмент дает годный размер,
вторым - брак,
- оба инструмента дают брак. Вероятность
гипотез:
- оба инструмента дает годные размеры,
- первый инструмент дает брак, второй -
годный размер,
- первый инструмент дает годный размер,
вторым - брак,
- оба инструмента дают брак. Вероятность
гипотез:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Наблюдалось событие А – деталь признана негодной. Поэтому
![]() .
.
Тогда вероятность гипотезы , после того как имело место событие А, то есть вероятность того, что деталь была признана негодной в результате обработки первым инструментом, определится по формуле Бейеса:

![]() .
.
Вероятность
![]() гипотезы
,
после того как имело место событие А,
то есть вероятность того, что деталь
была признана негодной в результате
обработки вторым инструментом, также
определится по формуле Бейеса:
гипотезы
,
после того как имело место событие А,
то есть вероятность того, что деталь
была признана негодной в результате
обработки вторым инструментом, также
определится по формуле Бейеса:

![]() .
.
Задание № 3.
Определить
точность процесса обработки и возможный
процент брака при тонком точении шейки
вала
![]() мм. Наметить пути снижения брака на
данной операции.
мм. Наметить пути снижения брака на
данной операции.
Измерения
деталей выборки (N=50)
показали, что рассеяние размеров
подчиняется нормальному закону
распределения с параметрами по данной
выборке
![]() (
(![]() - средний размер деталей выборки,
- средний размер деталей выборки,
![]() - среднее квадратическое отклонение
размеров).
- среднее квадратическое отклонение
размеров).
Теоретический материал для данного задания приводится в главе 3 [1].
Пример выполнения задания № 3.
Определить
точность процесса обработки и возможный
процент брака при тонком точении шейки
вала
![]() мм. Наметить пути снижения брака на
данной операции.
мм. Наметить пути снижения брака на
данной операции.
Измерения деталей выборки (N=50) показали, что рассеяние размеров подчиняется нормальному закону распределения с параметрами по данной выборке .
РЕШЕНИЕ.
В соответствии с заданным номиналом и предельными отклонениями на контролируемый размер, наименьший допускаемый диаметр шейки вала равен
![]() =25,0-0,033=24,967
мм,
=25,0-0,033=24,967
мм,
а наибольший допускаемый диаметр
![]() =25,0+0=25,0
мм.
=25,0+0=25,0
мм.
При этом величина допуска на размер определится как
![]() =0,033
мм.
=0,033
мм.

Рисунок 1. Определение вероятного процента брака.
Действительное
поле рассеивания размеров
![]() шеек валов в соответствии с правилом
3
будет равно
шеек валов в соответствии с правилом
3
будет равно
![]() ,
,
где
![]() - наименьший фактический размер получаемых
шеек валов, а
- наименьший фактический размер получаемых
шеек валов, а
![]() -
наибольший фактический размер.
-
наибольший фактический размер.
Точность
процесса обработки определяется
коэффициентом точности
![]() :
:
![]() .
.
При
![]() точность процесса избыточная,
точность процесса избыточная,
![]() – достаточная и
– достаточная и
![]() – недостаточная.
– недостаточная.
В данном случае
![]() ,
,
следовательно, точность процесса обработки недостаточная и появление брака неизбежно.
На
рисунке 1 вертикальная прямая, проходящая
через центр группирования
![]() ,
является осью симметрии. Она делит
площадь, ограниченную кривой нормального
распределения и осью абсцисс, и равную
единице, на две равные части. Размеры
шеек, лежащие на оси абсцисс левее
и правее
,
является осью симметрии. Она делит
площадь, ограниченную кривой нормального
распределения и осью абсцисс, и равную
единице, на две равные части. Размеры
шеек, лежащие на оси абсцисс левее
и правее
![]() выходят за поле допуска Т и валы с такими
размерами шеек отходят в брак. При этом
размеры, лежащие левее
,
дают неисправимый брак, а размеры,
лежащие правее
,
дают исправимый брак. Как видно из
рисунка 1 диаметров шеек валов, меньших,
чем
практически нет, так как наименьший
допустимый размер
шейки вала меньше
выходят за поле допуска Т и валы с такими
размерами шеек отходят в брак. При этом
размеры, лежащие левее
,
дают неисправимый брак, а размеры,
лежащие правее
,
дают исправимый брак. Как видно из
рисунка 1 диаметров шеек валов, меньших,
чем
практически нет, так как наименьший
допустимый размер
шейки вала меньше
![]() ,
определяющего левую границу поля
действительного рассеивания размеров.
Диаметры же большие, чем
имеются, так как наибольший допустимый
размер
шейки вала меньше
,
определяющего левую границу поля
действительного рассеивания размеров.
Диаметры же большие, чем
имеются, так как наибольший допустимый
размер
шейки вала меньше
![]() ,
определяющего правую границу поля
действительного рассеивания размеров.
Следовательно, есть вероятность появления
брака (в данном случае исправимого).
Вероятность Бисп
появления исправимого брака можно
представить как вероятность расположения
размера шейки вала левее точки
,
определяющего правую границу поля
действительного рассеивания размеров.
Следовательно, есть вероятность появления
брака (в данном случае исправимого).
Вероятность Бисп
появления исправимого брака можно
представить как вероятность расположения
размера шейки вала левее точки
![]() ,
равной 0,5, минус вероятность его попадания
в интервал (
,
),
равной
,
равной 0,5, минус вероятность его попадания
в интервал (
,
),
равной
![]() .
Здесь
.
Здесь
![]() – функция Лапласа.
– функция Лапласа.
Вероятное значение исправимого брака, выраженного в процентах, будет равно:
 .
.
Подставляя значения и используя таблицу приложения 2 [2], получаем
![]() ,
,
Расположение
поля допуска T
определяется номинальным размером
шейки вала
![]() =25,0
мм, а положение кривой распределения –
значением величины центра рассеяния
=25,0
мм, а положение кривой распределения –
значением величины центра рассеяния
![]() .
Значение
.
Значение
![]() определяется настроечным размером
станка, следовательно, изменяя настроечный
размер, можно изменять положение кривой
распределения вдоль оси абсцисс, изменяя
тем самым процент вероятного появления
исправимого и неисправимого брака. Если
ширина поля допуска T
больше или равна величине действительного
поля рассеяния размеров
(T≥
Δ), то появление брака можно избежать,
назначив настроечный размер так, чтобы
действительное поле рассеяния размеров
было расположено внутри поля допуска.
Если же ширина поля допуска меньше
ширины поля рассеяния размеров (T<
Δ), то появление брака неизбежно. В
рассматриваемом случае T=0,033
мм, а
=0,036
мм, поэтому брак неизбежен. Минимальный
процент вероятного брака будет тогда,
когда настроечный размер
совпадает со срединой поля допуска, т.
е.
определяется настроечным размером
станка, следовательно, изменяя настроечный
размер, можно изменять положение кривой
распределения вдоль оси абсцисс, изменяя
тем самым процент вероятного появления
исправимого и неисправимого брака. Если
ширина поля допуска T
больше или равна величине действительного
поля рассеяния размеров
(T≥
Δ), то появление брака можно избежать,
назначив настроечный размер так, чтобы
действительное поле рассеяния размеров
было расположено внутри поля допуска.
Если же ширина поля допуска меньше
ширины поля рассеяния размеров (T<
Δ), то появление брака неизбежно. В
рассматриваемом случае T=0,033
мм, а
=0,036
мм, поэтому брак неизбежен. Минимальный
процент вероятного брака будет тогда,
когда настроечный размер
совпадает со срединой поля допуска, т.
е.
![]() .
.
Так
как настроечный размер
![]() =24,99
мм, то станок требует подналадки -
уменьшения настроечного размера на
величину b=24,99-24,9835=0,0065
мм. При новом настроечном размере
=24,99
мм, то станок требует подналадки -
уменьшения настроечного размера на
величину b=24,99-24,9835=0,0065
мм. При новом настроечном размере
![]() =24,9835
мм процент вероятного исправимого и
неисправимого брака будет одинаковым
и общий процент брака можно определить
как:
=24,9835
мм процент вероятного исправимого и
неисправимого брака будет одинаковым
и общий процент брака можно определить
как:

Таким образом, корректировкой настроечного размера удается снизить вероятный процент брака с 4,75% до 0,6%.
Задание № 4.
Задание 4. 1. На двух токарных полуавтоматах изготавливают втулки. Результаты измерения 10 деталей, изготовленных на 1-м станке и 8 деталей, изготовленных на 2-м станке следующие:
![]() 30,0i;
30,12; 30,24; 30,18; 30,20; 30,08; 30,16; 29,98; 30,00; 29,9j,
30,0i;
30,12; 30,24; 30,18; 30,20; 30,08; 30,16; 29,98; 30,00; 29,9j,
![]() 30,0j;
30,04; 30,06; 30,08; 30,05; 30,24; 29,98; 30,1i.
30,0j;
30,04; 30,06; 30,08; 30,05; 30,24; 29,98; 30,1i.
Проверить предположение о том, что станки обладают различной точностью.
Теоретический материал для данного задания приводится в 13 [2], [6].
Задание
4. 2. По
результатам измерения 5 валов, обработанных
на токарном полуавтомате сразу после
настройки и через некоторый промежуток
времени получены следующие значения
выборочных средних
![]() ,
,
![]() и исправленные выборочные дисперсии
и исправленные выборочные дисперсии
![]() ,
,
![]() .
Определить, изменился ли настроечный
размер.
.
Определить, изменился ли настроечный
размер.
Пример выполнения задания № 4.
Задание 4. 1. На двух токарных полуавтоматах изготавливают втулки. Результаты измерения 10 деталей, изготовленных на 1-м станке и 8 деталей, изготовленных на 2-м станке следующие:
30,02; 30,12; 30,24; 30,18; 30,20; 30,08; 30,16; 29,98; 30,00; 29,96,
30,02; 30,04; 30,06; 30,08; 30,05; 30,24; 29,98; 30,10.
Проверить предположение о том, что станки обладают различной точностью.
РЕШЕНИЕ.
В
качестве генеральных совокупностей X
и Y
будем рассматривать результаты измерений
деталей изготавливаемых на 1-м и 2-м
станках соответственно. Требуется
проверить предположение о том, что
станки обладают различной точностью.
Точность станков определяется дисперсией
рассеивания размеров. Поэтому требуется
сравнить между собой дисперсии
![]() и
и
![]() генеральных совокупностей X
и Y.
В качестве нулевой гипотезы примем
гипотезу о том, что величины
и
различаются незначимо:
генеральных совокупностей X
и Y.
В качестве нулевой гипотезы примем
гипотезу о том, что величины
и
различаются незначимо:
![]() .
В качестве альтернативной гипотезы
рассмотрим гипотезу о значимом различии
величин
и
:
.
В качестве альтернативной гипотезы
рассмотрим гипотезу о значимом различии
величин
и
:
![]() .
.
Проверку
гипотезы
проведем на основании критерия Фишера.
Для этого вычислим сначала выборочные
дисперсии
![]() и
и
![]() :
:
![]()
![]()
где:
![]() - объемы выборок,
- объемы выборок,
![]() - выборочные средние, равные
- выборочные средние, равные


![]() (30,02-30,094)2+(30,12-30,094)2+(30,24-30,094)2+(30,18-30,094)2+
(30,02-30,094)2+(30,12-30,094)2+(30,24-30,094)2+(30,18-30,094)2+
+(30,20-30,094)2+(30,08-30,094)2+(30,16-30,094)2+(29,98-30,094)2+
+(30,00-30,094)2+(29,96-30,094)2)/10 =0,0905
![]() (30,02-30,07)2+(30,04-30,07)2+(30,06-30,07)2++(30,08-30,07)2+
(30,02-30,07)2+(30,04-30,07)2+(30,06-30,07)2++(30,08-30,07)2+
+(30,05-30,07)2+(30,24-30,07)2+(29,98-30,07)2+(30,10-30,0- 7)2)/8 = 0,0052.
Вычисляем
исправленные выборочные дисперсии
![]() и
и
![]() :
:
![]() ,
,
![]() .
.
Найдем наблюдаемое значение критерия
Фишера
![]() равное отношению большей исправленной
выборочной дисперсии к меньшей:
равное отношению большей исправленной
выборочной дисперсии к меньшей:
 .
.
Задавшись уровнем значимости
![]() и вычислив значения степеней свободы
и вычислив значения степеней свободы
![]() ,
а также учтя вид альтернативной гипотезы
(
),
находим по таблице приложения 7 [2]
критическую точку
,
а также учтя вид альтернативной гипотезы
(
),
находим по таблице приложения 7 [2]
критическую точку
![]() распределения Фишера:
распределения Фишера:
![]() .
.
Как видно > . Поэтому нет оснований принять нулевую гипотезу. Следовательно, величины и различаются значимо и станки обладают различной точностью.
Задание
4. 2. По
результатам измерения 5 валов, обработанных
на токарном полуавтомате сразу после
настройки и через некоторый промежуток
времени получены следующие значения
выборочных средних
![]() ,
,
![]() и исправленные выборочные дисперсии
и исправленные выборочные дисперсии
![]() ,
,
![]() .
Определить, изменился ли настроечный
размер.
.
Определить, изменился ли настроечный
размер.
РЕШЕНИЕ.
Предположим,
в качестве нулевой гипотезы, что
настроечный размер станка не изменился,
то есть выборочные средние
![]() и
и
![]() различаются незначимо. В этом случае
вид нулевой гипотезы будет следующий:
различаются незначимо. В этом случае
вид нулевой гипотезы будет следующий:
![]() .
В качестве альтернативной гипотезы
примем гипотезу о том, что настроечный
размер станка изменился и выборочные
средние
и
различаются значимо:
.
В качестве альтернативной гипотезы
примем гипотезу о том, что настроечный
размер станка изменился и выборочные
средние
и
различаются значимо:
![]() .
Согласно условию задачи обработка валов
ведется на одном станке, что позволяет
предположить, что генеральные дисперсии
рассеивания размеров двух партий валов
одинаковы (точность станка не изменилась).
Тогда нулевую гипотезу
проверим по критерию Стьюдента.
.
Согласно условию задачи обработка валов
ведется на одном станке, что позволяет
предположить, что генеральные дисперсии
рассеивания размеров двух партий валов
одинаковы (точность станка не изменилась).
Тогда нулевую гипотезу
проверим по критерию Стьюдента.
Вычислим наблюдаемое значение критерия по формуле:
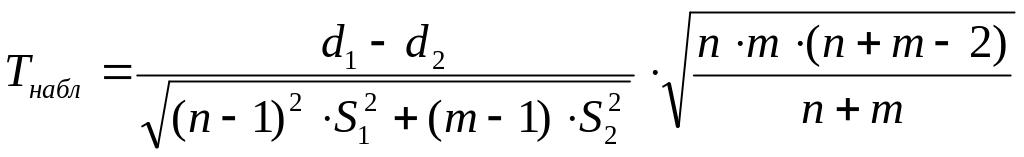
здесь
![]() - средние диаметры выборки;
- средние диаметры выборки;
![]() -
исправленные выборочные дисперсии;
n=m=5
– объемы выборки.
-
исправленные выборочные дисперсии;
n=m=5
– объемы выборки.
![]() .
.
Задавшись
уровнем значимости
![]() и числом степеней свободы
и числом степеней свободы
![]() найдем критическую точку
найдем критическую точку
![]() .
В данном случае альтернативная гипотеза
имеет вид
,
поэтому пользуясь таблицей распределения
Стьюдента (приложение 6 [2]) найдем
двухстороннюю критическую точку
.
В данном случае альтернативная гипотеза
имеет вид
,
поэтому пользуясь таблицей распределения
Стьюдента (приложение 6 [2]) найдем
двухстороннюю критическую точку
![]() .
Как видно
.
Как видно
![]() ,
что не дает основания отвергнуть нулевую
гипотезу. Таким образом можно утверждать,
что настроечный размер станка не
изменился.
,
что не дает основания отвергнуть нулевую
гипотезу. Таким образом можно утверждать,
что настроечный размер станка не
изменился.
Задание № 5.
Задание № 5.1.
При массовом производстве шестерен вероятность брака при штамповке равна 0,i. Какова вероятность того, что из 400 наугад взятых шестерен 5j будут бракованными.
Теоретический материал для данного задания приводится главе 3 [2], [1]/
Задание № 5.2.
Вероятность появления события за время испытаний P=0,i. Найти вероятность того, что событие появится : а) не менее 7j раз и не более 9j раз; б) не менее 7i раз; в) не более 7j раз при 100 испытаниях.
Пример выполнения задания № 5.
Задание 5. 1. При массовом производстве шестерен вероятность брака при штамповке равна 0,1. Какова вероятность того, что из 400 наугад взятых шестерен 50 будут бракованными.
РЕШЕНИЕ.
Используя локальную теорему Лапласа, имеем
![]()
Задание 5. 2. Вероятность появления события за время испытаний P=0,8. Найти вероятность того, что событие появится : а) не менее 75 раз и не более 90 раз; б) не менее 75 раз; в) не более 74 раз при 100 испытаниях.
РЕШЕНИЕ.
Если
вероятность появления события в
независимых испытаниях постоянна и
отлична от нуля и единицы, то вероятность
того, что в n
испытаниях событие произойдет от
![]() до
до
![]() раз определяется по формуле:
раз определяется по формуле:
![]()
где Ф(х) - функция Лапласа.

Учитывая, что функция Лапласа нечетна, т. е. Ф(-х)=-Ф(х), получим
P100(75;90)=Ф(5)-Ф(-1,25)=Ф(5)+Ф(1,25).
По таблице (Приложение 2 ) найдем
Ф(5)=0,499; Ф(1,25)=0,394.
Искомая вероятность данного события равна
P100(75; 90)=0,499+0,394=0,893.
б) требование, чтобы событие появилось не менее 75 раз, означает, что число появления события может быть равно 75, либо 76, ..., либо 100. Таким образом, в рассматриваемом случае следует принять k1=75, k2=100. Тогда

Ф(1,25)=0,394, Ф(5)=0,5.
Искомая вероятность равна
P100(75; 100)=Ф(5)-Ф(-1,25)=0,5+0,394=0,894.
в) события «А появилось не менее 75 раз» и «А появилось не более 74 раз» противоположны, поэтому сумма вероятностей этих событий равна единице. Следовательно, искомая вероятность
P100(0; 74)=1-P100(75; 100)=1- 0,894=0,106.
Задание № 6.
По
результатам контроля шлифованных шеек
валов определить среднее значение
параметра шероховатости
![]() ,
выборочное среднее квадратическое
отклонение
,
выборочное среднее квадратическое
отклонение
![]() и исправленное выборочное среднее
квадратическое отклонение
и исправленное выборочное среднее
квадратическое отклонение
![]() для заданной выборки в предположении,
что рассеивание значений параметра
шероховатости подчиняется нормальному
закону. Задавшись доверительной
вероятностью
для заданной выборки в предположении,
что рассеивание значений параметра
шероховатости подчиняется нормальному
закону. Задавшись доверительной
вероятностью
![]() определить доверительные интервалы
для величины среднего значения параметра
шероховатости
определить доверительные интервалы
для величины среднего значения параметра
шероховатости
![]() и величины среднего квадратического
отклонения
.
и величины среднего квадратического
отклонения
.
№ детали в выборке |
Значение параметра шероховатости Ra, мкм |
1. |
0,7i |
2. |
0,6j |
3. |
0,7j |
4. |
0,72 |
5. |
0,76 |
6. |
0,64 |
7. |
0,6i |
8. |
0,70 |
9. |
0,61 |
10. |
0,8j |
Теоретический материал для данного задания приводится в главе 10 [2.
Пример выполнения задания № 6.
По результатам контроля шлифованных шеек валов определить среднее значение параметра шероховатости , выборочное среднее квадратическое отклонение и исправленное выборочное среднее квадратическое отклонение для заданной выборки в предположении, что рассеивание значений параметра шероховатости подчиняется нормальному закону. Задавшись доверительной вероятностью определить доверительные интервалы для величин и .
№ детали в выборке |
Значение параметра шероховатости Ra, мкм |
1. |
0,75 |
2. |
0,68 |
3. |
0,78 |
4. |
0,72 |
5. |
0,76 |
6. |
0,64 |
7. |
0,60 |
8. |
0,70 |
9. |
0,61 |
10. |
0,81 |
РЕШЕНИЕ.
Объем
приведенной выборке равен 10. Тогда
среднее значение
![]() параметра шероховатости определится
как:
параметра шероховатости определится
как:

Выборочная
дисперсия
![]() находится по формуле:
находится по формуле:

Исправленная выборочная дисперсия будет равна:
![]()
Выборочное среднее квадратическое отклонение определится как:
![]()
Исправленное среднее квадратическое отклонение будет равно:
![]()
Интервальной
оценкой (с надежностью
![]() )
среднего значения
генеральной совокупности по выборочной
средней
при известном среднем квадратическом
отклонении
служит доверительный интервал
)
среднего значения
генеральной совокупности по выборочной
средней
при известном среднем квадратическом
отклонении
служит доверительный интервал
![]() ,
,
где
![]() - точность оценки,
- точность оценки,
![]() - значение аргумента функции Лапласа
- значение аргумента функции Лапласа
![]() при котором
при котором
![]() ,
определяемое по таблицам функции
Лапласа.
,
определяемое по таблицам функции
Лапласа.
При неизвестном среднем квадратическом отклонении генеральной совокупности и при объеме выборке меньше 30, доверительный интервал среднего значения определяется как
![]() ,
,
где
– исправленное выборочное среднее
квадратическое отклонение,
![]() ,
находят по таблицам по заданному объему
выборки
,
находят по таблицам по заданному объему
выборки
![]() и надежности
.
и надежности
.
В данном случае объем выборки меньше 30, поэтому
![]() .
.
Здесь значение принято в соответствии с таблицей приложения 3 [2].
Таким образом доверительный интервал среднего значения параметра шероховатости шлифованных валов будет равен:
![]()
или
![]() .
.
Интервальной оценкой (с надежностью ) среднего квадратического отклонения генеральной совокупности по исправленному выборочному среднему квадратическому отклонению служит доверительный интервал:
![]() ,
,
где
величина
![]() определяется по таблицам по заданным
и
.
определяется по таблицам по заданным
и
.
В
соответствии с таблицей приложения 3
[2] при
![]() и
величина
и
величина
![]() .
Следовательно, искомый доверительный
интервал будет:
.
Следовательно, искомый доверительный
интервал будет:
![]()
или
![]()
Задание № 7.
По результатам замеров содержания вредных веществ (гексана), выделяющихся из смазывающих - охлаждающих технологических сред (СОТС) в процессе механической обработки заготовок определить вероятность превышения допустимых норм. Допустимые нормы концентрации вредных веществ задаются интервалом: 21i мг/м3– 30j мг/м3.
Данные по концентрации вредных веществ, представлены в виде следующей выборки:
10i; 78; 126,8; 80,i; 2i; 107; 36,i; 11j; 35,6; 96; 80; 89; 3j,8; 126; 12,8; 82; 78,j; 126,3; 100; 78; 11j; 24,7; 126; 95; 113; 78,j; 150,3; 82; 36,i; 10j; 9j; 35,8; 112; 1j0,3; 82; 109; 35,j; 98; 126,3; 97; 112; 78,8; 126,9; 78,j; 104; 82; 10i; 78,8; 126,8; 1j,5; 100; 36,i; 103; 96; 89; 80; 10i; 13; 98; 80Д; 104; 96; 126; 78; 15i; 89; 14,6; 109; 37; 126,8; 82; 150,3; 3j,5; 126,9; 96; 35,8; 110; 80; 9j; 79; 17,2; 103; 78; 9j; 109,8; 10i; 35,3; 10j; 79,8; 170; 98; 78,6; 126; 82; 100; 36,2; 10i; 80,1; 110,4; 36; 10j; 78; 95; 108; 104,7; 80; 97; 104.
Теоретический материал для данного задания приведен в [4].
Для подтверждения корректности и правомочности производимых процедур, статистика на всех этапах расчета, предполагает проведение анализа (и, фактически, проверки) того, что делается, а именно:
- на этапе обработки информации необходимо, в случае, если имеются результаты, резко отличающиеся от основной массы данных, проверить, следует ли учитывать эти результаты, т.е. принадлежат ли они данной выборке, или их нужно отбросить;
- на этапе получения выборочных статистических характеристик, когда обрабатываются несколько отдельных выборок, объем каждой из которых слишком мал, встает вопрос о том, можно ли эти выборки объединить. То есть, фактически, нужно установить, относятся ли полученные статистики к единой генеральной совокупности. Если это так, то все эти выборки можно объединить в одну, более представительную, и полученные статистики будут обладать большей достоверностью;
- конечной целью статистических расчетов является получение закона распределения исследуемой случайной величины. В большинстве случаев предполагается один, реже два, три варианта законов распределения, окончательный выбор которого делается с помощью соответствующих критериев, которые называются критерии согласия.
Методически, каждая из этих проверок проводится по одной и той же схеме:
- постановка задачи - какой вид проверки рассматривается;
- формулировка положения, которое проверяется (выдвижение нулевой гипотезы);
- выбор критерия (или критериев), с помощью которого проверяется нулевая гипотеза.
Нулевая
гипотеза -
это гипотеза (обозначается -
![]() ),
предполагающая благоприятный исход
опыта.
),
предполагающая благоприятный исход
опыта.
Нулевую
гипотезу выдвигают, а затем проверяют
с помощью статистических критериев с
целью выявления оснований для ее
отклонения и для принятия альтернативной
гипотезы
![]() .
.
Например,
при решении вопроса о принадлежности
резко выделяющегося значения данной
выборке, нулевой или исходной гипотезой
при использовании критериев является
предположение о том, что наибольшее
значение
![]() (или наименьшее
(или наименьшее
![]() )
принадлежит
к той же генеральной совокупности, как
и все остальные
)
принадлежит
к той же генеральной совокупности, как
и все остальные
![]() результатов.
результатов.
Если имеющийся статистический материал не позволяет отвергнуть нулевую гипотезу, то ее принимают и используют в качестве рабочей гипотезы до тех пор, пока новые накопленные результаты не позволяют ее отклонить.
Нулевая гипотеза отклоняется тогда, когда на основании выборочных испытаний получается маловероятный результат для случая истинности выдвинутой нулевой гипотезы.
Границей между высокой и малой вероятностью служат так называемые уровни значимости.
Для большинства областей научного
исследования в качестве уровней
значимости принимают 5-% и 1-%-ый уровни.
Значительно реже используется
0,1%-ный уровень значимости (![]() =0,05
или
=0,01,
реже
=0,1
или
=0,001).
=0,05
или
=0,01,
реже
=0,1
или
=0,001).
Величина является уровнем значимости критерия и представляет вероятность отвержения нулевой гипотезы в том случае, если она верна (вероятность ошибки 1-го рода).
Таким образом, возможные исходы при проверке статистических гипотез могут быть следующими:
Решение по статистическому критерию |
Верно |
Неверно |
Н0 отвергается |
Ошибочное решение (ошибка 1-го рода) |
Правильное решение |
Н0 не отвергается |
Правильное решение |
Ошибочное решение (ошибка 2-го рода) |
Ошибка 2-го рода является более опасной, чем 1-го, так как гораздо хуже отвергнуть правильное решение, чем принять неправильное.
Если во время проведения эксперимента наблюдается резкое отклонение от нормы некоторых результатов и очевидны причины этого, то их следует просто исключить из дальнейшего рассмотрения.
Иногда причина резких отклонений опытных данных не ясна, однако полученный результат вызывает сомнение. В подобных случаях сомнительные результаты исключают (или не исключают) путем проверки с применением специальных критериев.
Первой
предварительной
проверкой является тот факт, находится
ли сомнительный
результат в интервале
![]() или нет.
или нет.
При
больших объемах, когда существует
уверенность в надежности оценки
среднего квадратического отклонения
![]() ,
а также в некоторых случаях
при малых выборках, когда величина
среднего квадратического отклонения
известна по результатам более ранних
испытаний, для решения вопроса
о принятии или исключении сомнительных
результатов целесообразно
использовать критерий Ирвина (
,
а также в некоторых случаях
при малых выборках, когда величина
среднего квадратического отклонения
известна по результатам более ранних
испытаний, для решения вопроса
о принятии или исключении сомнительных
результатов целесообразно
использовать критерий Ирвина (![]() ).
).
Для
этого вычисляют
![]() если
резко выделяющимся результатом является
последний
член вариационного ряда, и
если
резко выделяющимся результатом является
последний
член вариационного ряда, и
![]() если
- первый.
если
- первый.
Вычисленные
значения
сопоставляют
с критическим значением
![]() ,
найденным
теоретически для заданного уровня
доверительной вероятности
,
найденным
теоретически для заданного уровня
доверительной вероятности
![]() объема
выборки
объема
выборки
![]() .
(
- уровень
значимости). Величина
берется
из таблицы 7.1:
.
(
- уровень
значимости). Величина
берется
из таблицы 7.1:
Таблица 7.1. Значения величин
|
Значения при =... |
|||||||
2 |
3 |
10 |
20 |
30 |
50 |
… |
1000 |
|
0,10 |
2,3 |
1,8 |
1,2 |
1,0 |
1,0 |
0,9 |
… |
0,6 |
0,05 |
2,8 |
2,2 |
1,5 |
1,3 |
1,2 |
1,1 |
… |
0,8 |
0,01 |
|
|
|
|
|
|
… |
1,2 |
0,005 |
4 |
3,2 |
2,3 |
2,0 |
1,9 |
1,8 |
… |
1,4 |
Если
![]() ,
то отклонение величины механической
характеристики следует
считать случайным, т.е. оно вызвано лишь
проявлением неоднородности
свойств испытуемого объекта. В этом
случае нулевая гипотеза
подтверждается.
,
то отклонение величины механической
характеристики следует
считать случайным, т.е. оно вызвано лишь
проявлением неоднородности
свойств испытуемого объекта. В этом
случае нулевая гипотеза
подтверждается.
Если
![]() ,
то отмеченный выброс
,
то отмеченный выброс
![]() или
или
![]() не
случаен, не характерен
для рассматриваемой совокупности
данных, а определяется грубыми
ошибками в методике получения данных
или другими ошибками в
эксперименте.
не
случаен, не характерен
для рассматриваемой совокупности
данных, а определяется грубыми
ошибками в методике получения данных
или другими ошибками в
эксперименте.
Так
как нулевая гипотеза в этом случае
отклоняется, сомнительные значения
![]() или
или
![]() исключают из рассмотрения, а найденные
ранее статистики подвергают корректировке.
исключают из рассмотрения, а найденные
ранее статистики подвергают корректировке.
В
тех случаях, когда располагают лишь
статистиками рассматриваемой выборки,
целесообразно пользоваться критерием
Груббса (для малых выборок
![]() ).
).
Для этого, в зависимости от того, какой из крайних членов вариационного ряда является более сомнительным, определяют значения
![]() или
или
![]() ,
,
где - выборочное среднее квадратическое отклонение.
Вычисленные
значения сопоставляют с критическими
значениями, найденными из таблиц для
заданного уровня значимости
![]() и объема
выборки
.
и объема
выборки
.
Нулевую
гипотезу принимают, если
![]() и отвергают, если
и отвергают, если
![]() .
.
Критерий Груббса предназначен для случая нормального закона распределения случайной величины и действителен для наиболее широко встречающихся ситуаций, при которых генеральные параметры неизвестны, а известны лишь их оценки, полученные на основании полученной выборки.
Использование
критерий для отбрасывания при неизвестной
генеральной дисперсии (![]() )
возможно для нормального распределения
случайной величины при неизвестном
математическом ожидании и известном
значении генеральной дисперсии.
)
возможно для нормального распределения
случайной величины при неизвестном
математическом ожидании и известном
значении генеральной дисперсии.
Статистика критерия определяется как
![]() или
или
![]() ,
,
где - известная генеральная дисперсия.
Если
![]() или
или
![]() ,
то нулевая
гипотеза не отклоняется, т.е. результат
испытания
,
то нулевая
гипотеза не отклоняется, т.е. результат
испытания
![]() или
не следует
считать выбросом и он должен учитываться
, как и остальные
или
не следует
считать выбросом и он должен учитываться
, как и остальные
![]() результатов.
результатов.
В
противоположном случае при
![]() или
или
![]() ,
нулевая
гипотеза отклоняется, т.е. результат
или
является
ошибочным и должен быть исключен из
дальнейшего анализа, а найденные ранее
оценка математического ожидания должна
быть скорректирована.
,
нулевая
гипотеза отклоняется, т.е. результат
или
является
ошибочным и должен быть исключен из
дальнейшего анализа, а найденные ранее
оценка математического ожидания должна
быть скорректирована.
При решении ряда практических задач возникает необходимость определения значимости или случайности в расхождениях выборочных характеристик между собой, а также в расхождениях выборочных и известных генеральных характеристик.
Рассматриваемые ниже критерии (равенства дисперсий и равенства средних значений) предполагают, что исследуемые случайные величины распределены по нормальному закону или логнормальному. При других же законах распределения эти критерии некорректны, и их использование может привести к ошибочным результатам.
К критериям для установления принадлежности отдельных выборок одной и той же генеральной совокупности относится критерии для установления принадлежности отдельных выборок одной и той же генеральной совокупности. Статистикой критерия является величина
![]() .
.
В
некоторых практически важных случаях
имеющийся большой экспериментальный
материал позволяет с высокой точностью
и статистической надежностью оценить
генеральную дисперсию случайных величин
![]() .
.
Допустим,
что в условиях, несколько отличающихся
от предыдущих по ряду параметров, были
проведены исследования, получена
некоторая выборка значений случайных
величин и вычислена оценка дисперсии
исследуемой характеристики
![]() .
.
Требуется
проверить нулевую гипотезу
![]() ,
заключающуюся
в том, что дисперсия
генеральной совокупности, из которой
взята указанная выборка, равна
,
заключающуюся
в том, что дисперсия
генеральной совокупности, из которой
взята указанная выборка, равна
![]() (доказать
(доказать
![]() .
.
Рассмотрим
решение этой задачи при трех возможных
альтернативных гипотезах
![]() .
.
1.
Альтернативная гипотеза
![]() .
Если для выбранного уровня значимости
выполняется неравенство
.
Если для выбранного уровня значимости
выполняется неравенство

то нулевую гипотезу не отклоняют.
Если неравенство несправедливо, то нулевую гипотезу отвергают и принимают альтернативную гипотезу .
2.
Альтернативная гипотеза
![]() .
Нулевую
гипотезу
не отклоняют,
если выполняется неравенство
.
Нулевую
гипотезу
не отклоняют,
если выполняется неравенство

В случае несоблюдения неравенства нулевую гипотезу отвергают и принимают альтернативную .
3.
Альтернативная
гипотеза
![]() .
.
В этом случае для проверки нулевой гипотезы , используют двусторонний критерий. Если неравенства

справедливы, то нулевую гипотезу не отклоняют.
При невыполнении неравенства нулевую гипотезу отвергают и принимают альтернативную .
При использовании рассмотренных критериев, как и других критериев, важно, задаваясь приемлемой величиной уровня значимости обеспечить достаточно низкую вероятность ошибки 2-го рода, т.е. иметь достаточно высокую уверенность в браковке нулевой гипотезы в то время, когда верна альтернативная.
Другими словами, при проверке нулевой гипотезы должна быть обеспечена необходимая мощность критерия относительно альтернативной гипотезы.
Мощность одностороннего критерия в зависимости от фактического отклонения генеральных дисперсий
![]()
и принятого уровня значимости определяется из соотношения

где
![]() - максимальное относительное расхождение
(ошибка) в средних квадратических
отклонениях при принятии нулевой
гипотезы с уровнем значимости
- максимальное относительное расхождение
(ошибка) в средних квадратических
отклонениях при принятии нулевой
гипотезы с уровнем значимости
![]() -
вероятность
совершить ошибку 2-го рода, т.е. принять
неверную нулевую гипотезу.
-
вероятность
совершить ошибку 2-го рода, т.е. принять
неверную нулевую гипотезу.
Следующим критерием является критерий равенства дисперсий ряда совокупностей.
Нулевая
гипотеза в этом случае заключается в
том, что все m
генеральных совокупностей, из которых
взяты выборки, имеют равные дисперсии,
т.е.
![]() .
.
Наиболее
простым критерием проверки нулевой
гипотезы о равенстве (однородности)
ряда дисперсий
при одинаковых объемах выборок
![]() является критерий Хартлея, который
предусматривает вычисление статистики
является критерий Хартлея, который
предусматривает вычисление статистики

и
сопоставления ее с критическим значением
![]() для выбранного
,
числа партий
для выбранного
,
числа партий
![]() и
и
![]() .
.
При
выполнении неравенства
![]() нулевую гипотезу не отвергают, в противном
случае - отвергают и принимают
альтернативную гипотезу.
нулевую гипотезу не отвергают, в противном
случае - отвергают и принимают
альтернативную гипотезу.
Критерий
Кочрена (![]() )
используется также при равных объемах
отдельных выборок и является
предпочтительным по сравнению с критерием
Хартлея в случаях, когда одна из выборочных
дисперсий значительно больше остальных,
а также при
)
используется также при равных объемах
отдельных выборок и является
предпочтительным по сравнению с критерием
Хартлея в случаях, когда одна из выборочных
дисперсий значительно больше остальных,
а также при
![]() (m
- число выборок).
(m
- число выборок).
При использовании критерия Кочрена находят статистику

и
сопоставляют с критическим значением
![]() для выбранного
уровня значимости
,
числа партий
и
,
определяемого из таблиц.
для выбранного
уровня значимости
,
числа партий
и
,
определяемого из таблиц.
Если
выполняется неравенство
![]() ,
то нулевую
гипотезу не отвергают. При несоблюдении
этого неравенства нулевую гипотезу
отвергают и принимают альтернативную.
,
то нулевую
гипотезу не отвергают. При несоблюдении
этого неравенства нулевую гипотезу
отвергают и принимают альтернативную.
В связи с тем, что критерий Кочрена использует больше информации, он оказывается несколько более чувствительным, чем критерий Хартлея.
Критерий равенства дисперсий двух совокупностей – критерий Фишера (двусторонний F-критерий) использует статистику
 .
.
Пусть
по результатам испытаний двух независимых
выборок объемом
![]() и
и
![]() из нормально
распределенных совокупностей подсчитаны
оценки дисперсий
из нормально
распределенных совокупностей подсчитаны
оценки дисперсий
![]() и
и
![]() ,
причем
,
причем
![]() .
.
Требуется
проверить нулевую гипотезу о том, что
указанные выборки принадлежат генеральным
совокупностям с равными дисперсиями,
т.е.
![]() при
альтернативной гипотезе
при
альтернативной гипотезе
![]() .
.
С этой целью используют двусторонний F-критерий (критерий Фишера), для чего находят статистику
при
и
сопоставляют с критическим значением
![]() ,
определяемого из таблиц в зависимости
от
,
определяемого из таблиц в зависимости
от
![]() и
и
![]() для
для
![]() и
и
![]() .
.
Если
 выполняется, то нулевую гипотезу не
отвергают. В противном случае принимают
выполняется, то нулевую гипотезу не
отвергают. В противном случае принимают
![]() .
.
В
случае подтверждения нулевой гипотезы
по двум л
выборочным
дисперсиям производят оценку генеральной
дисперсии
![]() :
:
![]() ,
,
которая может быть использована для построения доверительных интервалов.
При
неодинаковом числе образцов в отдельных
партиях
![]() однородность может быть проверена с
помощью критерия Бартлета (
однородность может быть проверена с
помощью критерия Бартлета (![]() ).
В этом случае вычисляют
).
В этом случае вычисляют
 ,
,
где
 ,
,

и
сравнивают с табличным значением
![]() ,
найденным
для выбранного уровня значимости
и числа
степеней свободы
,
найденным
для выбранного уровня значимости
и числа
степеней свободы
![]() из таблиц..
из таблиц..
Если
выполняется условие
![]() ,
то нулевую
гипотезу о равенстве генеральных
дисперсий совокупностей, из которых
взяты выборки, не отвергают.
,
то нулевую
гипотезу о равенстве генеральных
дисперсий совокупностей, из которых
взяты выборки, не отвергают.
При неудовлетворении этого условия, нулевую гипотезу отвергают и принимают альтернативную.
Для сравнение выборочного среднего с известным генеральным средним, используют критерий
![]() .
.
Предполагается нормальное (логнормальное) распределение, однако в данном случае это требование является менее жестким.
Пусть
при наличии большого объема экспериментальных
данных были определены
![]() и
и
![]() .
.
Результаты
исследований при несколько измененных
условиях показали, что выборочные
значения
![]() и
и
![]() несколько отличаются от генеральных.
несколько отличаются от генеральных.
Требуется установить, имеется ли значимое различие между выборочным значением и генеральным средним .
Решение
этой задачи рассматривается для случаев,
когда генеральная дисперсия
![]() известна и
когда генеральная дисперсия
неизвестна,
но известна оценка
.
В качестве
нулевой гипотезы принимается предположение
о том, что
известна и
когда генеральная дисперсия
неизвестна,
но известна оценка
.
В качестве
нулевой гипотезы принимается предположение
о том, что
![]() .
Генеральная
дисперсия
сохранилась неизменной.
.
Генеральная
дисперсия
сохранилась неизменной.
Нулевую гипотезу не отклоняют, если выполняется неравенство:
При
альтернативе
![]()
![]() ,
(*)
,
(*)
При
альтернативе
![]() ,
,
![]()
где
![]() и
и
![]() - критические
значения одностороннего критерия для
уровня значимости
- критические
значения одностороннего критерия для
уровня значимости
![]() .
.
При нарушении условий приведенных выше условий нулевую гипотезу отвергают и принимают альтернативную.
При
альтернативной гипотезе
![]() используют двусторонний критерий
значимости.
используют двусторонний критерий
значимости.
Если выполняется неравенство
![]() ,
то нулевую
гипотезу не отвергают.
,
то нулевую
гипотезу не отвергают.
Для сравнения двух средних значений нормально (логнормально) распределенных совокупностей используют критерий Стьюдента (Госсета)
Пусть
из двух нормально распределенных
генеральных совокупностей с неизвестными
параметрами
![]() испытаны выборки объемом
испытаны выборки объемом
![]() ,
и
.
,
и
.
По
результатам испытаний подсчитаны оценки
параметров распределения
![]() .
.
Требуется
проверить нулевую гипотезу о равенстве
средних значений этих совокупностей,
т.е.
![]() ,
при
альтернативной гипотезе
,
при
альтернативной гипотезе
![]() .
.
Рассмотрим
вначале случай, когда дисперсии
генеральных совокупностей равны, т.е.
![]() (что может быть проверено по методике,
изложенной выше - критерий Фишера).
(что может быть проверено по методике,
изложенной выше - критерий Фишера).
Для
проверки нулевой гипотезы
вычисляют оценку дисперсии
![]() :
:
и статистику

Статистику
сопоставляют
с критическим значением
![]() ,
найденным для выбранного уровня
значимости
и числа
степеней свободы
,
найденным для выбранного уровня
значимости
и числа
степеней свободы
![]() из таблиц.
из таблиц.
Если
справедливо неравенство
![]() то нулевую
гипотезу не отвергают.
то нулевую
гипотезу не отвергают.
Если
![]() ,
то равенство двух средних проверяют с
помощью приближенного
- критерия:
,
то равенство двух средних проверяют с
помощью приближенного
- критерия:
 .
.
При этом число степеней свободы определяется из выражения:
![]() ,
,
где

Конечной целью любого статистического исследования является установление вида закона распределения изучаемой случайной величины, на основании которого можно прогнозировать поведение объекта или системы в дальнейшем.
В одних случаях закон распределения может быть установлен теоретически на основании выбранной модели рассматриваемого процесса. В других случаях функцию распределения выбирают априори.
Однако для получения надежных решений вероятностных задач в каждом отдельном случае необходима проверка соответствия опытных данных используемому закону распределения.
Одним из первых, наиболее простым, но весьма приближенным методом оценки согласия результатов эксперимента с тем или иным законом распределения является графический метод.
Опытные данные наносят на вероятностную бумагу и сравнивают с графиком принятой функции распределения, которая на вероятностной сетке изображается прямой линией. Если экспериментальные точки ложатся вблизи прямой со случайными отклонениями влево и вправо, то опытные данные соответствуют рассматриваемому закону распределения.
Систематические и значительные отклонения экспериментальных точек от аппроксимирующей прямой свидетельствуют об ошибочности принятой модели для обоснования закона распределения исследуемой случайной величины.
Графический способ в значительной степени является субъективным и используется на практике лишь в качестве первого приближения при решении этой задачи.
Существует большой ряд достаточно строгих аналитических критериев согласия результатов эксперимента выбранному ряду гипотетического распределения.
Однако при решении задач, связанных с исследованием характеристик (например, механических свойств) многие из них теряют свою универсальность в связи с тем, что параметры гипотетического распределения заранее неизвестны, и могут оцениваться лишь по результатам испытаний.
Если выбранный критерий согласия не позволяет сделать уверенный, однозначный вывод о соответствии опытных данных гипотетическому распределению, то необходимо провести проверку нулевой гипотезы по другому критерию.
Даже
при очень больших объемах выборок (![]() )
в ряде случаев нельзя
отдать предпочтение какому-либо одному
закону распределения. В этом случае
выбор распределения решается удобством
его применения в конкретной
задаче.
)
в ряде случаев нельзя
отдать предпочтение какому-либо одному
закону распределения. В этом случае
выбор распределения решается удобством
его применения в конкретной
задаче.
Критерий
согласия Пирсона (
)
применяют
для проверки гипотезы о соответствии
эмпирического
распределения предполагаемому
теоретическому распределению
![]() при
большом объеме выборки (
при
большом объеме выборки (![]() ).
).
Критерий применим для любых видов функции даже при неизвестных значениях их параметров. В этом заключается его универсальность.
Использование
критерия
предусматривает
разбиение размаха варьирования выборки
на интервалы и определение числа
наблюдений (частоты)
![]() для
каждого из
для
каждого из
![]() интервалов,
интервалов,
Для
удобства оценок параметров распределения
интервалы выбирают
одинаковой длины. Число интервалов
зависит от объема выборки.
Обычно принимают: при
![]() ;
при
;
при
![]() ;
при
;
при
![]() ;
при
;
при
![]() .
.
Интервалы,
содержащие менее пяти наблюдений,
объединяют с соседними.
Однако если число таких интервалов
составляет менее 20% от их общего
количества, допускаются интервалы с
частотой
![]() .
Статистикой
критерия Пирсона служит величина:
.
Статистикой
критерия Пирсона служит величина:
![]()
где
![]() -
вероятность попадания изучаемой
случайной величины в
-
вероятность попадания изучаемой
случайной величины в
![]() -ый
интервал, вычисляемая в соответствии
с гипотетическим законом распределения
.
-ый
интервал, вычисляемая в соответствии
с гипотетическим законом распределения
.
При
вычислении вероятности
нужно
иметь в виду, что левая граница
1-го интервала и правая граница последнего
должна совпадать с границами
области возможных значений случайной
величины. Например, при
нормальной законе распределения правый
интервал начинается в -
,
а
последний простирается до
![]() .
.
определяют
по соответствующей таблице для уровня
значимости
и
числа степеней свободы
![]() ,
здесь
,
здесь
![]() el
- число
интервалов после
объединения,
- число
параметров, оцениваемых по рассматриваемой
выборке.
el
- число
интервалов после
объединения,
- число
параметров, оцениваемых по рассматриваемой
выборке.
При
несоблюдении неравенства
![]() принимают альтернативную гипотезу о
принадлежности выборки неизвестному
распределению.
принимают альтернативную гипотезу о
принадлежности выборки неизвестному
распределению.
Недостатком
критерия Пирсона является потеря части
первоначальной
информации, связанная с необходимостью
группировки результатов
наблюдений в интервалы и объединения
отдельных интервалов
с малым числом наблюдений. В связи с
этим рекомендуется дополнять проверку
соответствия распределения по критерию
другими
критериями.
Это необходимо при объеме выборки
![]() .
.
Критерий
согласия
![]() этот
критерий используется при объемах
выборки
этот
критерий используется при объемах
выборки
![]() и
является
более мощным, чем критерий
,
однако при его применении требуется
больший объем вычислений.
и
является
более мощным, чем критерий
,
однако при его применении требуется
больший объем вычислений.
Поэтому
при
![]() этот критерий целесообразно использовать
только
в тех случаях, когда проверка гипотезы
по другим критериям не приводит к
безусловным выводам.
этот критерий целесообразно использовать
только
в тех случаях, когда проверка гипотезы
по другим критериям не приводит к
безусловным выводам.
Критерий базируется на распределении статистики, представляющей собой взвешенную сумму квадратов разностей между эмпирической и теоретической функцией распределения.
![]()
где
![]() - накопленная часть
- накопленная часть
![]()
где
![]() -
номер образца в вариационном ряду;
-
номер образца в вариационном ряду;
![]() -
оценка вероятности события
-
оценка вероятности события
![]() ;
;
- теоретическая (гипотетическая) функция распределения;
![]() -
весовая
функция.
-
весовая
функция.
Обычно весовую функцию используют двух видов:
1.
![]()
2.
![]() - этот вариант весовой функции применяют
в тех случаях, когда наибольшее значение
имеет соответствие эмпирической функции
распределения теоретической в области
крайних значений
случайной величины (на «хвостах»
распределения).
- этот вариант весовой функции применяют
в тех случаях, когда наибольшее значение
имеет соответствие эмпирической функции
распределения теоретической в области
крайних значений
случайной величины (на «хвостах»
распределения).
При использовании весовой функции в виде 1 статистику называют статистикой Смирнова, а в виде 2 - статистикой Андерсона-Дарлинга. Критерий применим для любых видов функций F(x), если известны значения их параметров.
Предлагаемая методика прогнозирования выходных характеристик технологической системы на основе обработки статистической информации представлена на рисунке 7.1.
После того, как произведен сбор информации, встает вопрос об ее объеме и тех выводах, которые можно сделать на ее основе. Необходимо отметить, что в ходе сбора информации могут возникать случайные и систематические ошибки. Они должны быть исключены при помощи критериев проверки, иначе выводы, сделанные на основе такой информации не могут быть достоверными.
Собранная на первом этапе информация представляет собой выборку определенного объема. Анализ количества имеющихся данных позволяет сделать вывод о том, расчеты какого уровня возможны .
Далее осуществляется определение выборочных характеристик и затем, если в выборке существуют данные, резко отличающиеся от основной массы, следует проверить, принадлежат ли они выборке или их можно отбросить, так как эти величины являются случайными ошибками.
Для этого применятся различные критерии для отбрасывания резко выделяющихся результатов, используя критерий Ирвина, критерий Груббса или t - критерий
На следующем этапе проводится построение гистограммы, по которой в дальнейшем будет происходить проверка вида закона распределения.

Рисунок 7.1. Алгоритм прогнозирования выходных характеристик системы
Построение гистограммы производится по следующему алгоритму:
1.
На первом этапе происходит систематизация
исходных данных, то есть производится
формирование вариационного ряда
![]() .
.
2.
Находят размах варьирования по формуле:
![]() .
.
3.
Выбирают число интервалов
![]() .
.
4.
Находят длину каждого интервала по
формуле:
![]() .
.
5. Строят прямоугольную систему координат. По оси абсцисс откладываются все интервалы, на которые разбит вариационный ряд (см. п. 3). Для этого на оси абсцисс проставляют первое значение вариационного ряда, затем к нему нужно прибавить найденную длину каждого интервала и также отметить на оси абсцисс. Повторяют эту операцию столько раз, пока не будут отмечены все интервалы.
6. Высота столбиков гистограммы - это количество значений вариационного ряда, попавших в каждый интервал.
После того как построена гистограмма, можно предположить кривую закона распределения, и соответственно проверить вид самого закона. Если рассматривать статистическую обработку, то этот этап является завершающим, так как имея закон распределения можно исследовать с любых позиций распределение случайной величины.
В нашем случае для расчетов по разработанной методике необходимо определение вероятности попадания исследуемого параметра в заданный интервал или же вероятности непревышения величиной предельно допустимого значения.
На следующем этапе алгоритма производится расчет вероятности безотказной работы или нахождения параметра в заданных пределах. Если мы имеем нормальный закон распределения, то это происходит по формулам и зависимостям, описанным выше. Если же имеет место какой- либо другой закон распределения, то существуют правила нахождения вероятности. К примеру, при логнормальном распределении полученная выборка должна быть сначала переведена в десятичные логарифмы, затем она проверяется на нормальность и, если гипотеза об этом подтверждается, то полученное распределение подчиняется логнормальному закону.
Когда построен закон распределения и определен вид кривой, то параллельно с этим этапом находится максимально (или минимально) допустимое значение исследуемой величины, исходя из условий функционирования системы.
Далее по закону распределения рассчитывается площадь под кривой и, соответственно, вероятность выполнения заданных условий.
На следующем этапе производится сравнение полученной расчетной вероятности с требуемой для данной конкретной системы и данных условий работы.
Если полученное значение больше заданного, то можно утверждать, что в системе не будет параметрического отказа и негативного влияния на технологическое оборудование, человека и окружающую среду.
Если же вероятность безотказной работы меньше требуемого уровня, то в системе с достаточно большой вероятностью произойдет отказ, т.е. выход исследуемого параметра за допустимые пределы, что может привести к серьезным последствиям.
Таким образом, в результате проведения расчетов по предложенной методике можно получить информацию о том, с какой вероятностью исследуемый параметр находится в допустимых пределах или же выходит за них.
Рассмотрим пути решения задачи, когда параметр превышает максимально допустимое значение или находится ниже минимально допустимого и причины, по которым это может произойти (Рисунок 7.2).
В первом случае необходимо проверить, нельзя ли изменить заданный максимум (или минимум). Так как вероятность нахождения изучаемой случайной величины в заданных пределах рассчитывается исходя из закона распределения, то, например, увеличивая значение максимально допустимой величины, можно получить большую вероятность выполнения необходимых условий, чем в предыдущем случае.

Рисунок 7.2.. Условия повторной проверки данных расчета.
Однако изменить предельно допустимое значение практически никогда не представляется возможным, так как это норматив, который не подлежит коррекции.
Следующий вариант заключается в повторной проверке статистической информации, на основе которой был проведен прогноз. Необходимо проанализировать условия сбора информации и возможность наличия систематических ошибок. Если эта гипотеза подтверждается, то производится сбор новой информации для тех же условий работы и расчет повторяется снова.
Если при расчете по каким-либо причинам не были исключены случайные ошибки, то они устраняются и в этом случае сбор новой информации не производится и далее расчет происходит в соответствии с алгоритмом.
Также необходимо отметить случай, когда возможно изменение условий работы системы, это может быть связано с диапазонами изменения температур, режимов нагружения и т.д. Тогда рассматриваемая система может начать функционировать в других условиях, более благоприятных, чем ранее и вредного влияния на другие объекты не произойдет. В этом случае также необходим повторный сбор статистической информации и расчет вероятности безотказной работы.
Четвертый вариант, при котором повторяется цикл расчета, происходит при изменении параметров самой системы. Это могут быть какие-либо конструктивные изменения или изменение величин параметров. В этом случае также необходим повторный сбор статистической информации, так как мы будем иметь дело с уже новой системой с другими параметрами и характеристиками.
Затем для последних двух случаев производится новый расчет вероятности и ее сравнение с нормативом.
Бывает ситуация, когда невозможно изменить ни параметры самой системы, ни условия ее функционирования, а вся информация, на основе которой осуществлялось прогнозирование, верна. При этом вероятность выхода исследуемого параметра за допустимые пределы достаточно высока и не удовлетворяет условиям работы. В этом случае после проведения процедуры прогнозирования необходимо, если, например, речь идет о повышенной концентрации вредных веществ в рабочей зоне, еще до начала работы, поставить дополнительное фильтрационное оборудование, которое будет предотвращать и устранять вредные выбросы.
В
каждом случае, когда полученное значение
![]() не
удовлетворяет условиям надежности
системы, становится возможным снова
повторить предложенную последовательность
действий и добиться нужного результата.
не
удовлетворяет условиям надежности
системы, становится возможным снова
повторить предложенную последовательность
действий и добиться нужного результата.
Пример выполнения задания № 7
Пусть интервал допустимых норм концентрации задан виде 200 мг/м3 – 300 мг/м3, а выборка:
101; 78; 126,8; 80,1; 21; 107; 36,1; 115; 35,6; 96; 80; 89; 35,8; 126; 12,8; 82; 78,5; 126,3; 100; 78; 115; 24,7; 126; 95; 113; 78,5; 150,3; 82; 36,1; 105; 95; 35,8; 112; 150,3; 82; 109; 35,5; 98; 126,3; 97; 112; 78,8; 126,9; 78,5; 104; 82; 101; 78,8; 126,8; 15,5; 100; 36,1; 103; 96; 89; 80; 101; 13; 98; 80Д; 104; 96; 126; 78; 151; 89; 14,6; 109; 37; 126,8; 82; 150,3; 35,5; 126,9; 96; 35,8; 110; 80; 95; 79; 17,2; 103; 78; 95; 109,8; 101; 35,3; 105; 79,8; 170; 98; 78,6; 126; 82; 100; 36,2; ИЗ; 80,1; 110,4; 36; 105; 78; 95; 108; 104,7; 80; 97; 104.
Вариационный ряд выборки будет:
12,8; 13; 14,6; 15,5; 17,2; 21; 24,7; 35,3; 35,5; 35,5; 35,6; 35,8; 35,8; 35,8; 36; 36,1; 36,1; 36,1; 36,2; 37; 78; 78; 78; 78; 78; 78,5; 78,5; 78,5; 78,6; 78,8; 78,8; 79; 79,8; 80; 80; 80; 80; 80,1; 80,1; 80,1; 82; 82; 82; 82; 82; 82; 89; 89; 89; 95; 95; 95; 95; 95; 96; 96; 96; 96; 97; 97; 98; 98; 98; 100; 100; 100; 101; 101; 101; 101; 103; 103; 104; 104; 104; 104,7; 105; 105; 105; 107; 108; 109; 109; 109,8; 110; 110,4; 112; 112; ИЗ; 113; 115; 115; 126; 126; 126; 126; 126,3; 126,3; 126,8; 126,8; 126,8; 126,9; 126,9; 150,3; 150,3; 150,3; 151; 170.
Как
видно
![]() ,
,
![]() .
.
Размах
варьирования
![]() .
.
Число
интервалов
![]() положим
равным 7 (обычно принимают
положим
равным 7 (обычно принимают
![]() ).
).
Длина
каждого интервала составляет
![]() .
.
Количество значений вариационного ряда в каждом интервале равно:
Номер интервала: |
Количество значений: |
1 |
7 |
2 |
13 |
3 |
20 |
4 |
30 |
5 |
22 |
6 |
11 |
7 |
5 |
Таким образом, имеем следующие границы интервалов:
Номер интервала: |
Граница интервалов |
1 |
12,8 – 35,26 |
2 |
35,26 – 57,72 |
3 |
57,72 – 80,18 |
4 |
80,18 – 102,64 |
5 |
102,64 – 125,1 |
6 |
125,1 – 147,56 |
7 |
147,56 - 170 |
Когда необходимые данные найдены, строится гистограмма, представленная на рисунке 2.

Рисунок 2. Гистограмма выборки.
Определяются середины интервалов как половины от суммы границ интервалов.
Номер интервала: |
Значение середины интервала |
1 |
24,03 |
2 |
46,49 |
3 |
68,95 |
4 |
91,41 |
5 |
113,87 |
6 |
136,33 |
7 |
1158,79 |
Найдем
среднее значение
![]() ,
дисперсию
,
дисперсию
![]() среднее
квадратическое отклонение
:
среднее
квадратическое отклонение
:
 ,
,
![]() ,
,
![]() .
.
Для удобства вычислений составим таблицу
№ интервала |
Граница |
середины |
число наблюдений |
|
|
|
1 |
12,80 |
35,26 |
24,03 |
7 |
1,56 |
282,65 |
2 |
35,26 |
57,72 |
46,49 |
13 |
5,60 |
227,47 |
3 |
57,72 |
80,18 |
68,95 |
20 |
12,77 |
80,95 |
4 |
80,18 |
102,64 |
91,41 |
30 |
25,39 |
0,76 |
5 |
102,64 |
125,10 |
113,87 |
22 |
23,20 |
119,52 |
6 |
125,10 |
147,56 |
136,33 |
11 |
13,89 |
222,96 |
7 |
147,56 |
170,00 |
158,78 |
5 |
7,35 |
222,61 |
Таким
образом, имеем:
![]() ,
,
![]() .
.
Следовательно,
![]() и
и
![]() .
.
Тогда:
левая граница трехсигмового интервала:
![]() ,
,
правая граница трехсигмового интервала:
![]() .
.
Как видно, первое и последнее значение вариационного ряда не выходят за рамки трехсигмового интервала, поэтому проверка отбрасывания резковыделяющихся элементов вариационного ряда не требуется.
Теперь
необходимо осуществить проверку вида
закона распределения. Это целесообразно
делать с помощью критерия согласи
Пирсона
![]() ,
так как объем выборки
,
так как объем выборки
![]() .
.
Статистикой критерия Пирсона служит величина
![]()
где:
![]() -
количество
наблюдений в каждом интервале;
-
количество
наблюдений в каждом интервале;
- объем выборки;
![]() -
вероятность
попадания случайной величины в
-й
интервал.
-
вероятность
попадания случайной величины в
-й
интервал.
Для того чтобы обеспечить удобство вычисления , необходимо произвести нормирование функции нормального распределения, то есть перейти к функции Лапласа. Функция Лапласа представляет интеграл с переменным верхним пределом вида
 -
-
Для удобства его вычисления составляется таблицы:
№ интервала |
Граница |
|
|
|
|||
1 |
12,80 |
35,26 |
24,03 |
-∞ |
-1,60 |
-0,500 |
-0,4450 |
2 |
35,26 |
57,72 |
46,49 |
-1,60 |
-0,94 |
-0,4450 |
-0,3265 |
3 |
57,72 |
80,18 |
68,95 |
-0,94 |
-0,28 |
-0,3265 |
-0,1105 |
4 |
80,18 |
102,64 |
91,41 |
-0,28 |
0,38 |
-0,1105 |
0,1480 |
5 |
102,64 |
125,10 |
113,87 |
0,38 |
1,04 |
0,1480 |
0,3510 |
6 |
125,10 |
147,56 |
136,33 |
1,04 |
1,70 |
0,3510 |
0,4555 |
7 |
147,56 |
170,00 |
158,78 |
1,70 |
+∞ |
0,4555 |
0,5000 |
№ интервала |
Граница |
|
|
|
|
|
1 |
12,80 |
35,26 |
0,0550 |
5,94000 |
1,0600 |
0,189 |
2 |
35,26 |
57,72 |
0,1185 |
12,79800 |
0,2020 |
0,003 |
3 |
57,72 |
80,18 |
0,2160 |
23,32800 |
-3,3280 |
0,475 |
4 |
80,18 |
102,64 |
0,2585 |
27,91800 |
2,0820 |
0,155 |
5 |
102,64 |
125,10 |
0,2030 |
21,92400 |
0,0760 |
0,000 |
6 |
125,10 |
147,56 |
0,1045 |
11,28600 |
-0,2860 |
0,007 |
7 |
147,56 |
170,00 |
0,0445 |
4,80600 |
0,1940 |
0,008 |
|
|
|
1,00 |
|
|
0,84 |
В
соответствии с таблицей приложения 5
[2] при
![]() значение
значение
![]() дает с вероятностью 0,99 то, что нулевую
гипотезу о том, что закон распределения
является нормальным, следует принять.
дает с вероятностью 0,99 то, что нулевую
гипотезу о том, что закон распределения
является нормальным, следует принять.
Предельно допустимая концентрация в области рабочей зоны равна 300 мг/м3, но концентрация в 200 мг/м3, оказывает негативное воздействие на здоровье рабочего персонала. Поэтому необходимо определить вероятность возникновения такой концентрации.
Нормальный закон распределения является симметричным, поэтому дисперсия и среднее значение остаются прежними.
Итак:
![]() ,
,
![]() ,
,
![]() .
.
Левой границей интервала будет значение 200, правой - 300. Переходим к функции Лапласа:
![]() ,
,
![]() .
.
Значения функций Лапласа заданного аргумента находятся из таблицы приложения 2 [2]:
![]() ,
,
![]() ,
,
![]() .
.
Следовательно,
![]() .
.
Как видно из примера, вероятность достижения концентрации гексана значения в пределах от 200 до 300 мг/м3 , равная 0,0007 не велика, и можно сделать прогноз, что применение данного вида СОТС при сохранении текущих условий работы не будет вредным.
Задание № 8.
По
заданным условиям (таблица 8.1), матрице
планирования и результатов эксперимента
(таблица 8.2) построить
математическую модель в виде уравнения
регрессии влияния
режимов обкатывания заготовки роликом
(продольной
подачи S,
мм/мин; скорости обкатки V,
м/мин; усилия деформирования Р, кН,) на
значение параметра шероховатости
![]() .
.
Таблица 8.1 - Условия эксперимента
Пределы варьирования |
Факторы (обозначения) |
||
Продольная подача S, мм/мин,
|
Скорость обработки V, м/мин,
|
Усилие деформирования Р, кН,
|
|
Основной
уровень
|
0,3 |
25,3 |
2,5 |
Шаг
варьирования
|
0,1 |
12,2 |
0,8 |
Верхний
уровень
|
0,4 |
37,5 |
3,0 |
Нижний
уровень
|
0,2 |
13,1 |
2,0 |
Таблица 8.2 - Матрица планирования и результаты эксперимента
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
11 |
1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
0,9i |
2 |
-1 |
+1 |
+1 |
-1 |
-1 |
+1 |
0,8j |
3 |
+1 |
-1 |
+1 |
-1 |
+1 |
-1 |
0,8i |
4 |
-1 |
-1 |
+1 |
+1 |
-1 |
-1 |
1,1j |
5 |
+1 |
+1 |
-1 |
+1 |
-1 |
-1 |
1,2i |
6 |
-1 |
+1 |
-1 |
-1 |
+1 |
-1 |
1,2j |
7 |
+1 |
-1 |
-1 |
-1 |
-1 |
+1 |
1,4i |
8 |
-1 |
-1 |
-1 |
+1 |
+1 |
+1 |
1,3j |
9 |
0 |
0 |
0 |
0 |
0 |
0 |
1,2i |
10 |
0 |
0 |
0 |
0 |
0 |
0 |
1,3j |
11 |
0 |
0 |
0 |
0 |
0 |
0 |
1,2i |
12 |
0 |
0 |
0 |
0 |
0 |
0 |
1,3j |
Теоретический материал для данного задания приводится в [5].
Наибольшее влияние на шероховатость поверхности при накатывании оказывают следующие параметры (факторы) (режимы обработки): продольная подача S, мм/об, скорость обработки V, м/мин., усилие деформирования Р, кН.
Предлагается алгоритм построения регрессионных моделей влияния указанных режимов обработки на достигаемую шероховатость обрабатываемых поверхностей осей, путем статистического анализа экспериментальных данных.
Порядок модели до реализации эксперимента неизвестен. В этом случае применяется последовательное планирование эксперимента, т.е. используется свойство композиционности. Это свойство плана позволяет разделить эксперимент на несколько этапов и постепенно переходить от простых моделей к сложным, используя результаты предыдущих опытов.
На первом этапе выдвигается гипотеза о линейности уравнения регрессии, т.е.
![]() .
.
На основе данных, полученных в результате реализации эксперимента, проверяется адекватность линейной модели. Если линейная модель неадекватна, то выдвигается гипотеза о значимом влиянии парных взаимодействий факторов:
![]()
Вычисляются параметры данной модели и производится проверка ее адекватности. Если модель такого типа неадекватна, то выполненные ранее опыты дополняют новой серией, позволяющей вычислить коэффициенты модели квадратичной типа:

где
![]() - значения i-го
и; j-го
параметров режима поверхностного
пластического деформирования (ППД);
- значения i-го
и; j-го
параметров режима поверхностного
пластического деформирования (ППД);
![]() - коэффициенты
уравнения; i,
j
- номера
факторов (параметров режима ППД), i=j;
i,j
= 1, 2, 3 (Р,
S,
V).
- коэффициенты
уравнения; i,
j
- номера
факторов (параметров режима ППД), i=j;
i,j
= 1, 2, 3 (Р,
S,
V).
Для упрощения обработки результатов эксперимента факторы (параметры режима обработки ППД) нормализуют по формуле:
![]()
где
![]() -
нормализованное значение фактора
-
нормализованное значение фактора
![]() ,
на верхнем или нижнем уровне;
,
на верхнем или нижнем уровне;
- действительное значение фактора;
![]() -
значение фактора на основном уровне;
-
значение фактора на основном уровне;
![]() -
интервал варьирования i-го
фактора.
-
интервал варьирования i-го
фактора.
Верхний уровень нормализованного фактора равен (+1), нижний - (-1), а основной нулю.
Эксперимент, в котором используют все возможные сочетания уровней, называется полным факторным экспериментом (ПФЭ). При числе уровней каждого фактора равном двум, число опытов ПФЭ составляет N = 2k.
В рассматриваемом случае N = 23 = 8. Вычисление параметров нормализованной линейной модели производится по формулам:
![]()
![]()
где
![]() -
параметр нормализованной модели (i=
1, 2, 3...k);
-
параметр нормализованной модели (i=
1, 2, 3...k);
k - число контролируемых факторов;
u - номер опыта (или серии опытов) (u = 1, 2, 3,..., N);
N - число опытов (или серий параллельных опытов);
Yu - значение функции отклика в u-м опыте;
![]() -
значение
-
значение
![]() в u-oм
опыте.
в u-oм
опыте.
Все параметры линейной модели определяются с одинаковой дисперсией:
![]()
где
![]() -
дисперсия воспроизводимости.
-
дисперсия воспроизводимости.
Если в каждой серии проводилось по m параллельных опытов, то
![]()
где N - число серий опытов в плане; u - номер серии опытов;
j - номер параллельного опыта в серии;
Yu - среднее значение отклика в u-й серии.
Если параллельные опыты отсутствуют, то для определения дисперсии воспроизводимости в центре плана проводится серия из m параллельных опытов.
Тогда
![]()
где
![]() - значение
функции отклика (исследуемой характеристики
шероховатости) в j-ом
опыте серии
(j=1,
2, 3, ..., m);
- значение
функции отклика (исследуемой характеристики
шероховатости) в j-ом
опыте серии
(j=1,
2, 3, ..., m);
![]() -
среднее
арифметическое значение для
.
-
среднее
арифметическое значение для
.
Доверительный интервал для параметров линейной модели
![]()
где
![]() - значение
критерия Стьюдента,
- значение
критерия Стьюдента,
Р - заданный уровень достоверности значений .
Для рассматриваемого случая
![]() .
.
Параметр
считается статистически значимым, если
его абсолютная величина больше
доверительного интервала:
![]() .
Статистически незначимые параметры
считаем равными нулю.
.
Статистически незначимые параметры
считаем равными нулю.
В
зависимости от наличия сведений о
дисперсии воспроизводимости эксперимента
![]() проверку
адекватности уравнения регрессии можно
производить по двум схемам. Первая из
них применяется при отсутствии оценки
дисперсии воспроизводимости, что
характерно для пассивного эксперимента,
и состоит из следующих этапов:
проверку
адекватности уравнения регрессии можно
производить по двум схемам. Первая из
них применяется при отсутствии оценки
дисперсии воспроизводимости, что
характерно для пассивного эксперимента,
и состоит из следующих этапов:
- вычисление дисперсии относительно среднего значения параметра оптимизации (остаточной дисперсии для уравнения нулевого порядка):
 ;
;
- расчет дисперсии, характеризующей отклонение экспериментальных значений величин от найденных по уравнению регрессии. Если порядок уравнения заранее неизвестен, то в случае многофакторного пространства начинают с уравнения первого порядка:

где
![]() - значение
параметра, вычисленное по уравнению
регрессии для условий i-ro
опыта;
- значение
параметра, вычисленное по уравнению
регрессии для условий i-ro
опыта;
f=N-g - число степеней свободы;
g
- число
коэффициентов регрессии; для линейного
уравнения g
= k+1;
для неполного
квадратного уравнения, включающего
члены типа
![]() и
и
![]() ,
,
![]() ;
для полного
квадратного уравнения
;
для полного
квадратного уравнения
![]() ;
;
k - число факторов;
- расчет отношения указанных дисперсий:

Если
![]() то модель
неадекватна. Здесь
то модель
неадекватна. Здесь
![]() и
и
![]() - числа степеней свободы.
- числа степеней свободы.
Затем
вычисляют коэффициенты уравнения
регрессии в виде полинома первой степени
(линейная модель). Для этого уравнения
определяют значение
![]() и вычисляют
отношение:
и вычисляют
отношение:

Затем
проверяют значимость этого отношения
.
Если и новая модель неадекватна, переходят
к модели более высокого порядка. Процедуру
повторяют до тех пор, пока не будет
выполнено
условие
![]() .
.
Индекс г соответствует степени предпоследнего полинома.
Если известна дисперсия воспроизводимости эксперимента, для оценки адекватности модели вначале рассчитывают дисперсию адекватности
 ,
,
а
затем определяется расчетное значение
критерия
![]() :
:

Если
![]() ,
модель считается адекватной для принятой
доверительной
вероятности Р,
чисел
степеней свободы дисперсии адекватности
,
модель считается адекватной для принятой
доверительной
вероятности Р,
чисел
степеней свободы дисперсии адекватности
![]() ,
и дисперсии воспроизводимости
,
и дисперсии воспроизводимости
![]() .
В противном случае модель неадекватна.
.
В противном случае модель неадекватна.
В
данном случае дисперсия вопроизводимости
![]() известна.
Число степеней свободы
дисперсии адекватности при k
= 3:
известна.
Число степеней свободы
дисперсии адекватности при k
= 3:
- для линейной модели:
![]() ;
;
- для модели, учитывающей парные взаимодействия:
![]() ;
;
- для модели учитывающей квадратичный характер зависимости:
![]() .
.
Число
степеней свободы
![]() для дисперсии воспроизводимости
для дисперсии воспроизводимости
![]() .
Вычисление
параметров нормализованной модели с
парными и тройными взаимодействиями
производится по формулам:
.
Вычисление
параметров нормализованной модели с
парными и тройными взаимодействиями
производится по формулам:
![]() ;
;
![]() ;
;
![]() .
.
Проверка статистической значимости параметров математической модели линейного типа и ее адекватности проводится так же, как и модели квадратичной зависимости.
Если
линейная модель и модель с парными
зависимостями неадекватны, в план
проведенных опытов, который называется
«ядром» эксперимента, добавляется
некоторое количество специальным
образом расположенных точек. Добавленные,
или «звездные» точки плана находятся
на расстоянии «звездного» плеча
от центра плана. Общее число опытов
![]() ,
при k
факторах
(в нашем случае
k
=
3)
,
при k
факторах
(в нашем случае
k
=
3)
![]() ,
,
где N - число опытов «ядра» плана (N = 8);
2z - число «звездных» точек (2z=2 - 3 = 6);
![]() -
число опытов в центре плана.
-
число опытов в центре плана.
Ортогональность плана заключается в выборе такого количества точек факторного пространства для измеряемого отклика, которое приводит к упрощению вычисления параметров модели. В этом случае значения каждого параметра модели вычисляются независимо от значений других параметров.
Значения параметров модели квадратичного типа вычисляются по формулам:


![]() ,
,
где
![]() .
При
.
При
![]() ,
тогда
,
тогда
![]() .
.
В числителе формул находятся суммы значений функции отклика и значений нормализованного фактора в соответствующем столбце, а в знаменателе - сумма квадратов значений нормализованных факторов из соответствующих столбцов.
Дисперсия оценок параметров модели определяется по формулам:
 ;
;
 ;
;
 ;
;
![]()
где - дисперсия воспроизводимости.
Доверительные
интервалы
![]() для параметров модели в данном случае
определяются
при помощи критерия Стьюдента:
для параметров модели в данном случае
определяются
при помощи критерия Стьюдента:
![]()
где
![]() - стандартное
отклонение, рассчитанное для каждого
из параметров модели.
- стандартное
отклонение, рассчитанное для каждого
из параметров модели.
Параметр
математической модели считается
статистически значимым, еcли
соблюдается соотношение
![]() .
.
Пример выполнения задания № 8
Пусть условиям, матрица планирования и результатов эксперимента заданы таблицами 8.3 и 8.4.
Таблица 8.3 - Условия эксперимента
Пределы варьирования |
Факторы (обозначения) |
||
Продольная подача S, мм/мин,
|
Скорость обработки V, м/мин,
|
Усилие деформирования Р, кН,
|
|
Основной уровень |
0,3 |
25,3 |
2,5 |
Шаг варьирования |
0,1 |
12,2 |
0,8 |
Верхний уровень |
0,4 |
37,6 |
3,0 |
Нижний уровень |
0,2 |
13,1 |
2,0 |
Таблица 8.4 - Матрица планирования и результаты эксперимента
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
11 |
1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
0,9 |
2 |
-1 |
+1 |
+1 |
-1 |
-1 |
+1 |
0,8 |
3 |
+1 |
-1 |
+1 |
-1 |
+1 |
-1 |
0,8 |
4 |
-1 |
-1 |
+1 |
+1 |
-1 |
-1 |
1,1 |
5 |
+1 |
+1 |
-1 |
+1 |
-1 |
-1 |
1,2 |
6 |
-1 |
+1 |
-1 |
-1 |
+1 |
-1 |
1,2 |
7 |
+1 |
-1 |
-1 |
-1 |
-1 |
+1 |
1,4 |
8 |
-1 |
-1 |
-1 |
+1 |
+1 |
+1 |
1,3 |
9 |
0 |
0 |
0 |
0 |
0 |
0 |
1,2 |
10 |
0 |
0 |
0 |
0 |
0 |
0 |
1,3 |
11 |
0 |
0 |
0 |
0 |
0 |
0 |
1,2 |
12 |
0 |
0 |
0 |
0 |
0 |
0 |
1,3 |
На первом этапе для поиска уравнения регрессии линейного типа был проведен полный факторный эксперимент типа 23, состоящий из восьми опытов. Результаты реализации матрицы планирования эксперимента сведены в таблицу 8.4.
По результатам эксперимента вначале считаются параметры нормализованной линейной модели вида
![]() ,
,
где:
![]() ,
,
-
нормализованное значение фактора
![]() на верхнем или нижнем уровне,
на верхнем или нижнем уровне,
- действительное значение фактора,
- значение фактора на основном уровне,
![]() -
интервал варьирования i-го
фактора,
-
интервал варьирования i-го
фактора,
![]()
![]()
![]()
![]()
Для
определения дисперсии воспроизводимости
было дополнительно проведено четыре
опыта с факторами на нулевом уровне
![]() .
Результаты опытов приведены в таблице
8.4 в строках 9 - 12. Как видно для них
.
Результаты опытов приведены в таблице
8.4 в строках 9 - 12. Как видно для них
![]() .
.
Тогда
дисперсия воспроизводимости
![]() равна:
равна:

а
дисперсия
![]() определения
параметров линейной модели определится
как
определения
параметров линейной модели определится
как
![]() .
.
Доверительный интервал для параметров линейной модели будет равен:
![]() ,
,
где
![]() - значение критерия Стьюдента определено
в соответствии с таблицей приложения
6 [2] при принятом уровне значимости 0,05.
- значение критерия Стьюдента определено
в соответствии с таблицей приложения
6 [2] при принятом уровне значимости 0,05.
Параметр
считается значимым, если его абсолютная
величина
больше модуля доверительного интервала
![]() :
.
Как видно, все параметры линейной модели
будут значимы.
:
.
Как видно, все параметры линейной модели
будут значимы.
Нормализованное уравнение линейной регрессии принимает вид:
![]() .
.
Действительное уравнение линейной регрессии в этом случае будет:
![]()
После преобразований:
![]() .
.
Для
проверки адекватности полученного
уравнения
линейной регрессии
определяется дисперсии адекватности
![]() :
:
 ,
,
где:
![]() - экспериментальное значение параметра
шероховатости в i-ом
опыте,
- экспериментальное значение параметра
шероховатости в i-ом
опыте,
![]() -
расчетное значение шероховатости по
линейному уравнению регрессии для
условий i-го
опыта,
-
расчетное значение шероховатости по
линейному уравнению регрессии для
условий i-го
опыта,
![]() -
число степеней свободы дисперсии
адекватности,
-
число степеней свободы дисперсии
адекватности,
![]() -
число опытов,
-
число опытов,
![]() -
число учитываемых параметров.
-
число учитываемых параметров.
Результаты расчета сводятся в таблицу 8.5.
Таблица 8.5 - Результаты расчета адекватности модели линейной регрессии.
Номер опыта |
Значения факторов |
Экспериментальные значения параметра |
Расчетные значения параметра |
|
||
|
|
|
||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
1 |
0,4 |
37,6 |
3 |
0,9 |
0,9 |
0,00 |
2 |
0,2 |
37,6 |
3 |
0,8 |
09 |
0,02 |
3 |
0,4 |
13,1 |
3 |
0,8 |
1,0 |
0,05 |
4 |
0,2 |
13,1 |
3 |
1,1 |
1,1 |
0,00 |
5 |
0,4 |
37,6 |
2 |
1,2 |
1,1 |
0,00 |
6 |
0,2 |
37,6 |
2 |
1,2 |
1,2 |
0,00 |
7 |
0,4 |
13,1 |
2 |
1,4 |
1,3 |
0,05 |
8 |
0,2 |
13,1 |
2 |
1,3 |
1,3 |
0,00 |
Сумма: |
0,012 |
|||||
Тогда дисперсия адекватности равна:
![]() .
.
Далее
определяем расчетное значение функции
Фишера
рассеивания
значений, как отношение дисперсии
![]() адекватности
линейного уравнения регрессии и дисперсии
воспроизводимости:
адекватности
линейного уравнения регрессии и дисперсии
воспроизводимости:

По
таблицам распределения значений функции
Фишера (таблица приложения 7 [2]) для
принятого уровня достоверности 0,95,
числа степеней свободы
![]() дисперсии адекватности и числа
степеней свободы
дисперсии адекватности и числа
степеней свободы
![]() дисперсии воспроизводимости, находим
критическое значение
дисперсии воспроизводимости, находим
критическое значение
![]() .
.
Уравнение
регрессии считается адекватным, если
<
![]() .
Сравнивая значения
и
,
убеждаемся, что
>
,
следовательно полученное уравнение
регрессии неадекватно.
.
Сравнивая значения
и
,
убеждаемся, что
>
,
следовательно полученное уравнение
регрессии неадекватно.
Переходим к уравнению регрессии вида
,
учитывающие парные влияния факторов на параметры шероховатости.
Определяем значения коэффициентов парных взаимодействий факторов:


Доверительный интервал для параметров рассматриваемого уравнения регрессии определится как:
![]()
Так как значения коэффициентов парных взаимодействий превышают по абсолютной величине доверительный интервал, то следует считать вычисленные параметры значимыми.
Тогда нормализованное уравнение регрессии с учетом парных взаимодействий имеет вид:
![]()
Действительное уравнение регрессии с учетом парных взаимодействий будет иметь вид:

После преобразований получаем:
![]()
Для
проверки адекватности полученного
уравнения
регрессии
с учетом парных взаимодействий
определяется дисперсии адекватности
![]() :
:
 ,
,
где
![]() - число степеней свободы для уравнения
регрессии, учитывающего парные
взаимодействия.
- число степеней свободы для уравнения
регрессии, учитывающего парные
взаимодействия.
Результаты расчета сводятся в таблицу 8.6.
Таблица 8.6 - Результаты расчета адекватности уравнения регрессии
Номер опыта |
Значения факторов |
Экспериментальные значения параметра |
Расчетные значения параметра |
|
||
|
|
|
||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
1 |
0,4 |
37,6 |
3 |
0,9 |
0,9 |
0,00 |
2 |
0,2 |
37,6 |
3 |
0,8 |
09 |
0,02 |
3 |
0,4 |
13,1 |
3 |
0,8 |
1,0 |
0,05 |
4 |
0,2 |
13,1 |
3 |
1,1 |
1,1 |
0,00 |
5 |
0,4 |
37,6 |
2 |
1,2 |
1,1 |
0,00 |
6 |
0,2 |
37,6 |
2 |
1,2 |
1,2 |
0,00 |
7 |
0,4 |
13,1 |
2 |
1,4 |
1,3 |
0,05 |
8 |
0,2 |
13,1 |
2 |
1,3 |
1,3 |
0,00 |
Сумма: |
0,012 |
|||||
Тогда дисперсия адекватности равна:
![]() .
.
Определяем
расчетное значение функции Фишера
рассеивания
значений, как отношение дисперсии
![]() адекватности
и дисперсии
воспроизводимости:
адекватности
и дисперсии
воспроизводимости:

По
таблицам распределения значений функции
Фишера для принятого уровня достоверности
0,95, числа степеней свободы
![]() дисперсии адекватности и числа
степеней свободы
дисперсии воспроизводимости, находим
критическое значение
дисперсии адекватности и числа
степеней свободы
дисперсии воспроизводимости, находим
критическое значение
![]() .
.
Уравнение регрессии считается адекватным, если < . Сравнивая значения и , убеждаемся, что > , следовательно, полученное уравнение регрессии адекватно и может быть принято.
