Аналитическая геометрия. Плоскость в пространстве.

Определение: Любой ненулевой вектор, перпендикулярный плоскости, называется вектором нормали к этой плоскости.

N= (A, B, C).

Пусть т. М₀ (x₀, y₀, z₀) - произвольная фиксированная точка плоскости α,

т. М (x, y, z) - произвольная нефиксированная точка плоскости α (текущая).

α

М₀

М

Вектор М₀М=(x- x₀, y- y₀, z- z₀) Є плоскости α.

Вектор N= (A, B, C)  плоскости α.

‪⇒ N  М₀М.

Из условия перпендикулярности двух векторов: N • М₀М= 0.

В координатной форме: A(x- x₀)+ B(y- y₀)+ C(z- z₀)= 0 – уравнение плоскости, проходящей через заданную точку перпендикулярно заданному вектору.

Раскроем в этом уравнении скобки и соберем свободные члены

Ax+By+Cz-Ax₀-By₀-Cz₀= 0.

Обозначим: D=-Ax₀-By₀-Cz₀.

Ax+ By+Cz+D= 0 ‒ общее уравнение плоскости, где N(A, B, C) – координаты вектора нормали.

Анализ общего уравнения.

1) А= 0, B, C, D ≠ 0, т.е. нет х, нормаль N=(0, B, C).

Скалярное произведение: N• i= 0· 1+ B· 0+ C· 0= 0. ⇒ N  i, N  OX.

Т.о. плоскость параллельна оси OX , т.е. α ║OX .

Аналогично, В=0, нет у, плоскость α║ОУ;

С=0, нет z, плоскость α║OZ .

2) А= В= 0; нет х, у; плоскость α║XOY;

A= C= 0; нет x, z; плоскость α║XOZ;

В= С= 0; нет y, z; плоскость α║YOZ.

3) D= 0: Ax+ By+ Cz= 0.

т. О (0, 0, 0) удовлетворяет уравнению, плоскость проходит через начало координат т. О(0, 0, 0).

4) A= D= 0, B≠ C≠ 0, т.е. нет х и проходит через т. О. ⇒ плоскость α проходит через ОХ.

Аналогично, B= D= 0, плоскость α проходит через ОУ;

C= D= 0, плоскость α проходит через OZ.

5) х= 0 - уравнение координатной плоскости YOZ;

y= 0 - уравнение координатной плоскости XOZ;

z= 0 - уравнение координатной плоскости XOY.

Уравнение плоскости, проходящей через 3 точки.

Аксиома: Через три точки, не лежащие на одной прямой, проходит единственная плоскость.

Пусть т. М₁(x₁, y₁, z₁), т. М₂ (x₂, y₂, z₂), т. М₃(x₃, y₃, z₃) Є плоскости.

Пусть т. М (x, y, z) - текущая точка плоскости.

M

Вектор М₁М= (х- x₁, y- y₁, z- z₁), М₁М₂= (x₂ - x₁, y₂ - y₁, z₂ - z₁),

М₁М₃= (x₃ - x₁, y₃ - y₁, z₃ - z₁).

Все вектора лежат в одной плоскости ⇒ векторы компланарны. Тогда смешанное произведение векторов М₁М·М₁М₂· М₁М₃= 0:

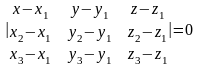- уравнение плоскости через три точки.

Уравнение плоскости в отрезках.

Пусть плоскость отсекает на координатных осях отрезки a – на оси ОХ, b – на оси ОУ, с – на оси OZ.

Тогда т. А (а, 0, 0), т. В (0, b, 0), т. C (0, 0, c) Є плоскости.

Тогда вектора AM (x- a, y, z), AB(-a, b, 0), AC(-a, 0, c) компланарны. Отсюда следует, что AM·AB·AC= 0.

.

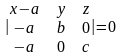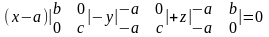
bc (x-a)+ acy+ abz= 0,

bcx+ acy+ abz= bac │: abc,

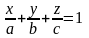- уравнение плоскости в отрезках.

Пример. Написать уравнение плоскости, проходящей через т. М₀ (2, -1, 3) перпендикулярно вектору N= (1, -1, 2), и построить плоскость.

Пример. Написать уравнение плоскости, проходящей через 3 точки

т. М₁(3, -2, 0), т. М₂ (4, 1, -3), т. М₃(2, 2, 1).

Взаимное расположение двух плоскостей.

1) Плоскость (1) с уравнением параллельна плоскости (2) с уравнением .

Отсюда следует, что ║ 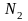. Координаты коллинеарных векторов пропорциональны.

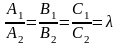- условие параллельности двух плоскостей.

Если 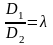, то такие плоскости будут совпадать.

2) Плоскость (1) перпендикулярна плоскости (2).

⇒  . Отсюда следует, что скалярное произведение • =0. - условие перпендикулярности двух плоскостей.

3) При пересечении двух плоскостей образуются две пары двухгранных углов.

Углом между двумя плоскостями считают угол между их векторами нормали: - угол между плоскостями.