Министерство образования и науки российской федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Национальный исследовательский ядерный университет «МИФИ»

Волгодонский инженерно-технический институт - филиал нияу мифи

Конспект лекций

по теме:

«Векторная алгебра и аналитическая геометрия»

Волгодонск

Линейные (векторные) пространства.

Определение: Множество L называется линейным (векторным) пространством, если на нем введены две операции:

1) сложение: для любых х, у Є L сумма (х + у) Є L,

2) умножение на число: для любого х Є L и любого числа λ произведение

λх Є L,

которые удовлетворяют 8 аксиомам:

1. х + у = у + х, где х,у Є L;

2. (х + у)+z = x+(у + z), где х,у,z Є L;

3. существует нулевой элемент Ө такой, что Ө + х = х, где х Є L;

4. для любого х Є L существует единственный противоположный элемент

(–х) такой, что х + (-х)= Ө;

5. 1·х = х, где х Є L;

6. α(βх) = (αβ)х, где х Є L, α и β- числа;

7. α(х + у) = αх + αу, где х,у Є L, α- число;

8. (α + β) х = αх + βх, где х Є L, α и β- числа.

Замечание: Элементы линейного (векторного) пространства называют векторами.

Примеры:

Множество действительных чисел является линейным пространством.

Множества всех векторов на плоскости и в пространстве являются линейным пространством.

Множество всех матриц одного размера является линейным пространством.

Линейная зависимость и независимость векторов линейного пространства.

Дана в линейном пространстве система векторов а_1, а_2, а_{3, …} а_n Є L.

Определение: Вектор α₁ а₁+ α₂ а₂+…+ α_n а_n Є L, где α_i (i = 1,…,n) - числа, называется линейной комбинацией(ЛК) векторов а_1, а_2, а_{3, …} а_n.

Определение: Система векторов линейного пространства а_1, а_2, а_{3, …} а_n Є L называется линейно независимой (ЛНЗ), если линейная комбинация

α₁ а₁+ α₂ а₂+α₃ а₃+…+ α_n а_n=0 тогда и только тогда, когда коэффициенты

α ₁ =α ₂ =α ₃ =…=α _n=0.

Определение: Система векторов а_1, а_2, а_{3, …} а_n Є L называется линейно зависимой (ЛЗ), если существует набор чисел α_1, α₂ ,α₃ … α_n, не все из которых равны 0, такие что линейная комбинация α₁ а₁+ α₂ а₂+…+ α_n а_n= 0.

Примеры:

Два вектора называются коллинеарными, если они параллельны одной прямой или лежат на одной прямой.

1) Рассмотрим два ненулевых, неколлинеарных вектора на плоскости. Диагональ =0 .

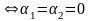а₁ α₁ а₁

Два ненулевых, не коллинеарных вектора на плоскости линейно независимы.

2) Рассмотрим два ненулевых , коллинеарных вектора а₁ ║а₂.

а₂

а₁

Линейная комбинация равна нулю, есть не нулевой коэффициент, следовательно, два коллинеарных вектора на плоскости линейно зависимы.

Теоремы о линейно зависимых системах векторов линейного пространства.

Теорема 1. Необходимое и достаточное условие линейной зависимости.

Для того чтобы система векторов линейного пространства была линейно зависимой необходимо и достаточно, чтобы какой-нибудь вектор этой системы был линейной комбинацией всех остальных.

Д ок-во: Необходимость ( ).

Дана ЛЗ система. Нужно доказать, что один вектор ЛК всех остальных.

а_1, а_2, а_{3, …} а_n – ЛЗ система векторов, т.е. среди α_1, α₂ ,α₃ … α_n существует число отличное от нуля так, что ЛК α₁ а₁+ α₂ а₂+α₃ а₃+…+ α_n а_n= 0.

Положим для определения, что коэффициент α₁ ≠ 0. Разделим обе части последнего равенства на α₁ ≠ 0:

;

.

Отсюда следует, что а₁ - ЛК остальных векторов.

Необходимость доказана.

Д остаточность ( ).

Пусть один вектор – это линейная комбинация остальных. Нужно доказать, что система векторов ЛЗ.

Пусть α_n = α₁ а₁+ α₂ а₂+α₃ а₃+…+ α_n-1 а_n-1.

α₁ а₁+ α₂ а₂+α₃ а₃+…+ α_n-1 а_n-1- 1α_n = 0.

Так как есть не нулевой коэффициент, то система векторов а_1, а_2, а_{3, …} а_n- линейно зависима.

Ч.т.д.

Теорема 2. Система, содержащая нуль-вектор, линейна зависима.

Док-во: Рассмотрим систему векторов, содержащую нуль-вектор. а_1, а_2, а_{3, …} а_n,Ө, где Ө ‒ нуль-вектор. Очевидно, что имеет место следующее равенство 0·а₁+ 0· а₂+0· а₃+…+ 5·Ө = 0.

Есть не равный нулю коэффициент, равный 5, а линейная комбинация равна 0, отсюда следует, что система векторов ЛЗ.

Ч.т.д.

Теорема 3. Система, содержащая линейно зависимую подсистему, тоже будет линейно зависима.

Док-во: Рассмотрим систему векторов а_1, а_2, …,а_к, а_{к+1 …} а_n, где а_1, а_2,…, а_к - линейно зависимый кусочек. α₁ а₁+ α₂ а₂+ … +α_ка_к= 0. Есть коэффициент отличный от нуля.

Очевидно, что с этими же коэффициентами будет выполняться равенство

α₁ а₁+ α₂ а₂+…+α_к а_к+…+0· а_к+1+…+ 0·α_n = 0.

Отсюда следует, что система векторов ЛЗ.

Ч.т.д.