
- •4.2. Дискретный спектр стационарного случайного процесса
- •4.3. Непрерывный спектр стационарного случайного процесса
- •4.4. Узкополосные и широкополосные случайные процессы
- •4.5. Взаимная корреляционная функция и взаимная спектральная плотность двух стационарных случайных процессов
- •Методические указания
4. СПЕКТРАЛЬНО-КОРРЕЛЯЦИОННАЯ ТЕОРИЯ
СТАЦИОНАРНЫХ СЛУЧАЙНЫХ ПРОЦЕССОВ
4.1. Основные свойства автокорреляционной функции
стационарного случайного процесса
Перечислим основные свойства автокорреляционной функции стационарного (в широком смысле) случайного процесса.
1. Автокорреляционная функция ССП является четной функцией, т.е.
![]()
Это свойство вытекает из симметричности корреляционной функции.
2. Значение автокорреляционной функции
при
![]() равно дисперсии ССП:
равно дисперсии ССП:
![]()
3. При
![]() значение автокорреляционной функции
стремится к нулю, т.е.
значение автокорреляционной функции
стремится к нулю, т.е.
![]()
4. Значение автокорреляционной функции
ССП при
всегда больше или равно ее значению при
![]() ,
т.е.
,
т.е.
![]()
Рис. 4.1. Корреляционная
функция стационарного случайного
процесса
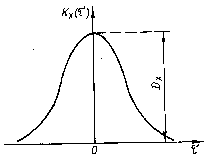
![]() к нулю при
не всегда происходит монотонно, могут
быть случаи, когда значения корреляционной
функции колеблются около нуля, приближаясь
к нулю при увеличении
к нулю при
не всегда происходит монотонно, могут
быть случаи, когда значения корреляционной
функции колеблются около нуля, приближаясь
к нулю при увеличении
![]() .
.
Отношение
![]()
называется нормированной корреляционной
функцией ССП. Величину
![]() иногда называют коэффициентом корреляции
ССП.
иногда называют коэффициентом корреляции
ССП.
Функция
обладает теми же свойствами, что и
автокорреляционная функция. Коэффициент
корреляции является четной функцией
аргумента. Максимальное значение
![]() соответствует
.
Выполняется неравенство
соответствует
.
Выполняется неравенство
![]() при любом
причем
при любом
причем
![]() при
.
при
.
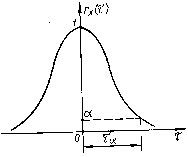
Рис. 4.2. Определение
интервала
корреляции
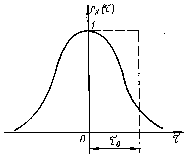
Рис. 4.3. Определение
интервала
корреляции
![]() ,
что при
,
что при
![]() >
случайные величины
>
случайные величины
![]() и
и
![]() для любого t
можно считать практически некоррелированными,
т.е.
для любого t
можно считать практически некоррелированными,
т.е.
![]() .
Величина
называется интервалом корреляции и
определяется либо долей
.
Величина
называется интервалом корреляции и
определяется либо долей
![]() от
(рис. 4.2), либо половиной ширины основания
прямоугольника единичной высоты, площадь
которого ровна площади под кривой
коэффициента корреляции (рис.4.3). В первом
случае для определения
от
(рис. 4.2), либо половиной ширины основания
прямоугольника единичной высоты, площадь
которого ровна площади под кривой
коэффициента корреляции (рис.4.3). В первом
случае для определения
![]() решают уравнение:
решают уравнение:
![]()
а во втором - для определения вычисляют интеграл:
![]()
4.2. Дискретный спектр стационарного случайного процесса
При анализе периодических детерминированных сигналов используется как временное, так и частотное представление этих сигналов. Переход от одного вида представления к другому осуществляется с помощью формул ряда Фурье.
Дискретным амплитудным спектром периодического детерминированного сигнала называется функция, описывающая распределение амплитуд по различным частотам. Амплитудный спектр показывает, какого рода гармоники преобладают в данном сигнале, какова его внутренняя структура.
Совершенно аналогичное спектральное описание может быть дано ССП. Разница заключается в том, что для ССП амплитуды колебаний будут случайными величинами.
Для избавления от случайности амплитуд гармоник усредняют спектральные разложения и рассматривают спектр дисперсий. При этом фазовые соотношения между спектральными составляющими не учитываются, поскольку при случайном процессе определенности в этих соотношениях нет.
Таким образом, дискретным спектром ССП называется распределение дисперсий амплитуд гармоник по различным частотам.
Дискретный спектр ССП определяется исходя из следующих соображений.
Рассмотрим ССП
![]() ,
наблюдаемый на интервале (0,Т). Пусть
задана автокорреляционная функция ССП
:
,
наблюдаемый на интервале (0,Т). Пусть
задана автокорреляционная функция ССП
:
![]()
Рис. 4.4.
Автокорреляционная функция
стационарного
случайного процесса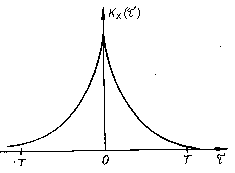
![]() есть четная функция:
есть четная функция:
=![]()
и, следовательно, на графике изобразится симметричной кривой (рис. 4.4.).
При изменении
![]() и
и
![]() от нуля до
T аргумент
от нуля до
T аргумент
![]() изменяется от минус Т до плюс
Т.
изменяется от минус Т до плюс
Т.
Автокорреляционную функцию (рис. 4.4.) ССП на интервале (-Т, Т) можно разложить в комплексный ряд Фурье, условно считая ее периодически повторяющейся:
![]() (4.1)
(4.1)
где
![]()
![]() (4.2)
(4.2)
Перейдем к тригонометрической форме
ряда Фурье. Предварительно докажем,
что коэффициенты
![]() ряда (4.1) удовлетворяют следующему
равенству:
ряда (4.1) удовлетворяют следующему
равенству:
![]() (4.3)
(4.3)
Действительно, воспользовавшись формулой Эйлера,
![]()
имеем:
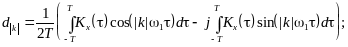
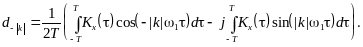
Функция является четной функцией, поэтому второй интеграл в выражениях (4.4) и (4.5) равен нулю как интеграл в симметричных пределах от нечетной функции. Следовательно, с учетом четности подинтегральной функции первого интеграла в выражениях (4.4) и (4.5) можно записать:
![]()
что и требовалось доказать.
Теперь выделим из ряда (4.1) пару слагаемых
из индексами
![]() и
и
![]() и учтем
соотношение (4.3).
и учтем
соотношение (4.3).
Получим для суммы этих слагаемых
![]()
![]() (4.7)
(4.7)
С учетом соотношения (4.7) ряд (4.1) преобразуется к виду:
![]() (4.8)
(4.8)
где
![]() (4.9)
(4.9)
![]() (4.10)
(4.10)
Смысл удвоения коэффициентов Фурье
![]() в тригонометрическом ряду при
в тригонометрическом ряду при
![]() становится ясным из рассмотрения
векторной диаграммы (рис. 4.5). Вещественная
функция
становится ясным из рассмотрения
векторной диаграммы (рис. 4.5). Вещественная
функция
![]() получается как сумма проекций на ось
абсцисс двух векторов
получается как сумма проекций на ось
абсцисс двух векторов
![]() .
.
Рис. 4.5. Представление
гармонической функции в виде
двух
комплексных
составляющих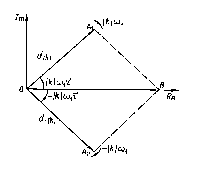
![]() во взаимно противоположных направлениях.
Суммарный вектор
во взаимно противоположных направлениях.
Суммарный вектор
![]() в любой момент времени совпадает с осью
действительных чисел. Вектор
в любой момент времени совпадает с осью
действительных чисел. Вектор
![]() ,
вращающийся против часовой стрелки,
соответствует положительной частоте,
а вектор
,
вращающийся против часовой стрелки,
соответствует положительной частоте,
а вектор
![]() ,
вращающийся по часовой стрелке -
отрицательной частоте. После перехода
к тригонометрической форме, понятие
"отрицательная частота" теряет
смысл. Поэтому как и в гармоническом
анализе детерминированных сигналов
отрицательная частота - понятие не
физическое, а математическое, вытекающее
из способа представления комплексных
чисел.
,
вращающийся по часовой стрелке -
отрицательной частоте. После перехода
к тригонометрической форме, понятие
"отрицательная частота" теряет
смысл. Поэтому как и в гармоническом
анализе детерминированных сигналов
отрицательная частота - понятие не
физическое, а математическое, вытекающее
из способа представления комплексных
чисел.
Перейдем в выражении для автокорреляционной функции (4.8) от аргумента к двум аргументам и . Для этого положим:
![]() (4.11)
(4.11)
и подставим выражение (4.11) в формулу (4.8):
![]() (4.12)
(4.12)
Из сравнения выражений (3.6) и(4.12) видно,
что формула (4.12) есть не что иное, как
каноническое разложение корреляционной
функции
![]() .
Координатными функциями этого
канонического разложения являются
попеременно косинусы и синусы частот,
кратных
.
Координатными функциями этого
канонического разложения являются
попеременно косинусы и синусы частот,
кратных
![]() :
:
![]()
По каноническому разложению автокорреляционных функций, как было указано ранее, можно построить каноническое разложение самого ССП:
![]() (4.13)
(4.13)
где
![]()
Из формулы (4.13) следует, что ССП на
ограниченном интервале времени можно
представить совокупностью гармонических
составляющих различных частот с
амплитудами, являющимися некоррелированными
случайными величинами, дисперсии которых
равны коэффициентам
![]() в спектральном разложении корреляционной
функции. Определим дисперсию ССП
заданного спектральным разложением
(4.13). По теореме о дисперсии линейной
функции некорреляционных случайных
величин
в спектральном разложении корреляционной
функции. Определим дисперсию ССП
заданного спектральным разложением
(4.13). По теореме о дисперсии линейной
функции некорреляционных случайных
величин
![]() (4.14)
(4.14)
Таким образом, дисперсия ССП равна сумме дисперсий всех гармоник его спектрального разложения.
Формула (4.14) представляет собой равенство Парсеваля для случайных сигналов и показывает, что мощность случайного сигнала равна сумме мощностей гармонических составляющих разложения (4.13).
На спектральной диаграмме ССП каждой
гармонике ставится в соответствие
вертикальный отрезок, длина которого
пропорциональна дисперсии ее амплитуды,
а расположение на оси абсцисс отвечает
частоте. В качестве примера на рис. 4.6,а
построен спектр дисперсий
![]() ,
а на рис. 4.6,б - спектр коэффициентов
для одного и того же ССП.
,
а на рис. 4.6,б - спектр коэффициентов
для одного и того же ССП.
Рис. 4.6. Дискретный
спектр дисперсии
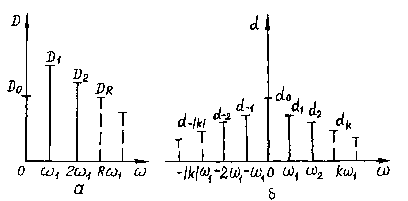
![]() (а)
и
коэффициентов
(б) стационарного
случайного
процесса
(а)
и
коэффициентов
(б) стационарного
случайного
процесса
Из рис. 4.6 видно, как при переходе от
разложения автокорреляционной функции
в тригонометрический ряд Фурье к ее
разложению в комплексный рад Фурье с
искусственным введением в рассмотрение
области отрицательных частот уменьшаются
в два раза значения коэффициентов
разложения (см. формулу (4.9)). Коэффициент
![]() не удваивается, так как в спектре
коэффициентов
составляющая с нулевой частотой не
имеет "дублера" (см. формулу (4.10)).
не удваивается, так как в спектре
коэффициентов
составляющая с нулевой частотой не
имеет "дублера" (см. формулу (4.10)).
