1. ЦЕЛЬ РАБОТЫ

Целью данной работы является: изучение математического ма­ятника (исследование зависимости периода колебаний математичес­кого маятника от его длины и массы) и определение ускорения сво­бодного падения с помощью оборотного маятника.

2. ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ

2.1. Математический маятник Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке. Достаточно хорошим прибли­жением к математическому маятнику будет устройство, представляю­щее собой небольшой тяжелый шарик, подвешенный на длинной тонкой нити (рис. 1).

Математический маятник

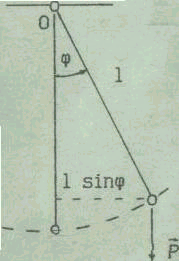
Рис. 1

Отклонение маятника от положения равновесия будем характе­ризовать углом , образованным нитью с вертикалью. На маятник действуют внешние силы: сила тяжести и реакция оси подвеса 0. При отклонении маятника от положения равновесия-возникает момент силы относительно оси 0, стремящийся вернуть маятник в положе­ние равновесия. Если сила лежит в плоскости, перпендикулярной данной оси, то ее момент относительно этой оси равен по величине произведению силы на плечо (расстояние от оси до прямой, вдоль которой действует сила). При повороте маятника на угол в одном направлении сила стремится вращать его в противоположном нап­равлении. Следовательно, знак момента силы относительно оси О противоположен знаку угла поворота маятника и sin .

Выражение для вращательного момента М, приложенного к маят­нику, имеет вид

М = -mg I sin . , (1)

где m - масса маятника;

В - ускорение свободного падения;

mg - сила тяжести (P=mg);

1 - длина маятника.

Величина 1 sin - плечо силы Р относительно оси 0.

Для исследования колебаний маятника воспользуемся основным законом динамики вращательного движения

J (2)

где J - момент инерции тела относительно оси вращения 0;

е - угловое ускорение тела (e=d² /dt², t - время);

М - результирующий момент (алгебраическая сумма моментов всех действующих на тело внешних сил относительно оси 0). Момент инерции J играет при вращательном движении тела та­кую же роль, какую масса при поступательном, т.е. является мерой инертности тела при вращательном движении, и характеризует рас­пределение массы по объему тела.

Момент инерции материальной точки относительно оси равен произведению массы точки на квадрат ее расстояния r от этой оси

J =mr² (3)

Для протяженных тел момент инерции определяется как сумма моментов инерции отдельных элементарных масс Δmi, на которые можно разбить тело, т.е.

J = или J= (4)

где интеграл распространяется на весь объем тела.

Момент инерции математического маятника относительно оси подвеса 0. согласно формуле (3), равен

J=ml² (5)

С учетом значений (1) и (5) основной закон динамики (2) для маятника приобретает вид "

(6)

Деля обе части равенства (6) на ml² и вводя обозначение

(7)

получим дифференциальное уравнение колебаний математического ма­ятника

(8)

Уравнение (8) нельзя проинтегрировать по времени при помощи элементарных функций. Поэтому мы ограничимся рассмотрением малых колебаний маятника, считая sin 0 Тогда вместо (8) будем иметь следующее приближенное дифференциальное уравнение малых колебаний маятника:

(9)

Общее решение этого уравнения имеет вид

где А и а - произвольные постоянные, определяемые по начальным условиям движения.

Величина А, т.е. наибольшее значение угла отклонения маятника от вертикали, называется амплитудой колебания,- sin о - циклической частотой ( , v - частота колебаний), аргумент ( )- фа­зой колебания, а величина - начальной фазой колебания (значе­ние фазы в начальный момент, т.е. при t=0).

Таким образом, при малых колебаниях угловое отклонение ма­тематического маятника изменяется со временем по гармоническому закону. При больших углах отклонения маятник будет совершать сложное колебательное движение. Как следует из уравнения (7) частота о при малых колебаниях маятника зависит от его длины и от ускорения свободного падения и не зависит от массы маятника. Период малых колебаний математического маятника, если заменить о него значением (7), будет определяться формулой

(10)

Период колебаний маятника при малых амплитудах не зависит от амплитуды. Это свойство называется изохронностью колебаний маятника (открыто Г. Галилеем - в 1583 г.).

Физический маятник

Физическим маятником называется твердое тело, которое может вращаться (качаться) вокруг неподвижной оси 0 под действием собс­твенного веса (рис. 2).

Рассмотрим колебания с учетом формы и расположения отдель­ных элементов массы маятника. На маятник, отклоненный от положе­ния равновесия, действуют внешние силы: сила тяжести и реакция оси подвеса 0. Трением в оси пренебрегаем. Реакция оси подвеса не имеет момента относительно оси вращения. Момент, стремящийся вернуть маятник в положение равновесия, равен

,

где m - масса маятника;

1 - расстояние между точкой подвеса 0 и центром масс маятни­ка С.