МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Кафедра ЭАФУ

Отчет по

лабораторной работе №5

Интерполирование функций заданных таблицей своих значений.

Вариант №25

Выполнил студент группы 0А14

Ларькин Дмитрий Александрович

Проверил преподаватель

Обходский Артем Викторович

Томск-2012

Цель работы

Ознакомиться с методом восстановления функциональных зависимостей – интерполяция. Научиться реализовывать данный метод программно на языке СИ и при помощи специализированных программных пакетов (Matcad).

Задание

1. Ознакомиться с описанием лабораторной работы №5 (электронная копия – в файле Численные методы.doс, размещенному по адресу L:\Методички\ Каф24\Информатика_140800\2_семестр\Методические указания).

2. Составить алгоритм решения задачи согласно своего варианта.

3. Составить блок-схему алгоритма программы.

4. Набрать текст программы на языке СИ при помощи текстового редактора.

5. Провести трансляцию и компоновку программы.

6. Решить контрольный пример.

7. Решить задачу с использованием пакета Matcad. Электронная копия методического пособия размещается в файле Методическое пособие по MathCad.doc размещенно по адресу L:\Методички\ Каф24\Информатика_140800\2_семестр\Методические указания).

8. Составить отчет по лабораторной работе.

Вариант 25

1. Составить программу интерполирования функции с использованием полинома Лагранжа.

2. Ввод исходных данных организовать через файлы.

3. Ввод аргумента, порядка полинома и длинны массива исходных данных организовать через терминал.

4. Максимальный возможный порядок интерполирующего полинома n<10.

5. Максимальное количество узлов интерполяции в массиве исходных данных m<121.

6. Результаты решения и исходные данные вывести в файл.

7. Предусмотреть возможность многократного ввода аргумента и порядка полинома.

Теоретическая часть Интерполяция, полином Лагранжа Общие положения.

В вычислительной практике часто приходится иметь дело с функциями 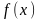, заданными таблицами их значений для некоторого конечного множества значений х: .

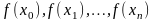В процессе же решения задачи необходимо использовать значения для промежуточных значений аргумента. В этом случае строят функцию Ф(x), достаточно простую для вычислений, которая в заданных точках x₀, x₁,...,x_n, называемых узлами интерполяции, принимает значения , а в остальных точках отрезка (x₀,x_n), принадлежащего области определения , приближенно представляет функцию с той или иной степенью точности.

При решении задачи в этом случае вместо функции оперируют с функцией Ф(x). Задача построения такой функции Ф(x) называется задачей интерполирования. Чаще всего интерполирующую функцию Ф(x) отыскивают в виде алгебраического полинома.

Интерполяционный полином.

Для каждой функции , определенной на [a,b], и любого набора узлов x₀, x₁,....,x_n( x_i 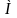[a,b], x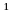_i x_j при i j ) среди алгебраических многочленов степени не выше n существует единственный интерполяционный многочлен Ф(x), который может быть записан в форме:

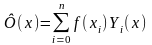, (1)

где 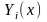- многочлен n-ой степени, обладающий следующим свойством:

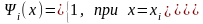
(2)

Для интерполяционного полинома многочлен имеет вид:

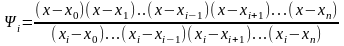(3)

Этот многочлен (1) и решает задачу интерполирования и называется интерполяционным полиномом Лагранжа.

1. Пример

В качестве примера рассмотрим функцию вида 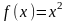на интервале 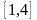заданную табличным способом.

X	1	2	3	4
F(x)	1	4	9	16

Необходимо определить значение функции в точке x-2.5. Воспользуемся для этого полином Лагранжа. Исходя из формул (1 и 3) запишем этот полином в явном виде:

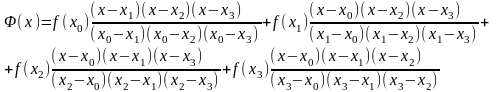(4).

Тогда подставляя в формулу (4) исходные значения из нашей таблицы получим

Полученный результат соответствует теории т.е. .

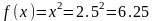Интерполяционная формула Лагранжа

Интерполяционный полином Лагранжа может быть записан в другой форме:

(5)

Запись полинома в виде (5) более удобна для программирования.

При решении задачи интерполяции величина n называется порядком интерполирующего полинома. При этом, как видно из формул (1) и (5), число узлов интерполирования всегда будет равно n+1 и значение x, для которого определяется величина , должно лежать внутри области определения узлов интерполяции т.е.

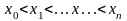. (6)

В некоторых практических случаях общее известное число узлов интерполяции m может быть больше, чем порядок интерполирующего полинома n.

В этом случае, прежде чем реализовывать процедуру интерполяции согласно формуле (5), необходимо определить те узлы интерполяции, для которых справедливо условие (6). При этом следует помнить, что наименьшая погрешность достигается при нахождении значения x в центре области интерполяции. Для обеспечения этого предлагается следующая процедура:

1. После ввода в программу значения величины х необходимо проверить условие x₀  x  x_m, где x₀ и x_m – начальное и конечное значение узловых точек интерполяции.

2. При выполнения предыдущего условия начинается поиск области интерполяции, для чего находим первое x_i такое, для которого выполняется условие x_i > x, при этом номер i будет соответствовать середине интервала интерполяции. Для определения области интерполяции ее левая граница будет начинаться с номера 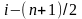, а заканчиваться узлом с номером .

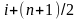3. После выполнения пунктов 1 и 2 программируется формула (5).

Основное назначение интерполяции – это вычисление значений табулированной функции для неузловых (промежуточных) значений аргумента, поэтому интерполяцию часто называют «искусством чтения таблиц между строками».

Описание алгоритма решения задачи

1. Программа запрашивает порядок полинома, х, количество точек, проверяя с помощью цикла do while соответствие с заданием. Если порядок полинома+1 больше, чем количество точек, то порядок уменьшается до максимально возможного.

2. С помощью цикла в массив с двумя столбцами записываются значения

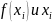
3. В файл сразу записываются значения, введенные с клавиатуры

4. Так как предполагается, что аргументы изначально упорядочены по возрастанию, поэтому выполняется проверка на то, чтобы искомый аргумент заключался между крайними.

5. Далее в случае, если порядок полинома+1 меньше, чем количество точек, то стартует цикл, выбирающий границы подсчета х в соответствии с порядком полинома.

6. Начинается вычисление значения значение функции от заданного х в соответствии с вышеуказанной формулой

7. Результат записывается в файл, после чего пользователю предлагается еще раз повторить процедуру.

Руководство программиста

Программный код приложения разрабатывался на языке СИ.

Блок-схема алгоритма программы приведена в приложении А.

Листинг программы приведен в приложении В.

Пример входного и выходного файла в приложении С.

Руководство пользователя

В каталоге с приложением должен находиться текстовой файл table.txt, в первом столбце которого находятся аргументы, а во втором соответствующие значения функции. Для корректной работы программы аргументы должны идти строго по возрастанию. Максимальное число строк-120. После запуска программа потребует значение аргумента, порядок полинома и количество считываемых точек. Не имеет смысла задавать порядок полинома больше, чем количество точек+1, а так же аргумент должен лежать в пределах определения функции. Процедуру можно повторять сколько угодно раз, после чего посмотреть результаты в файле FX.txt

Вывод: В ходе лабораторной работы был изучен метод восстановления функциональных зависимостей – интерполяция, а так же данный метод реализован программно на языке СИ

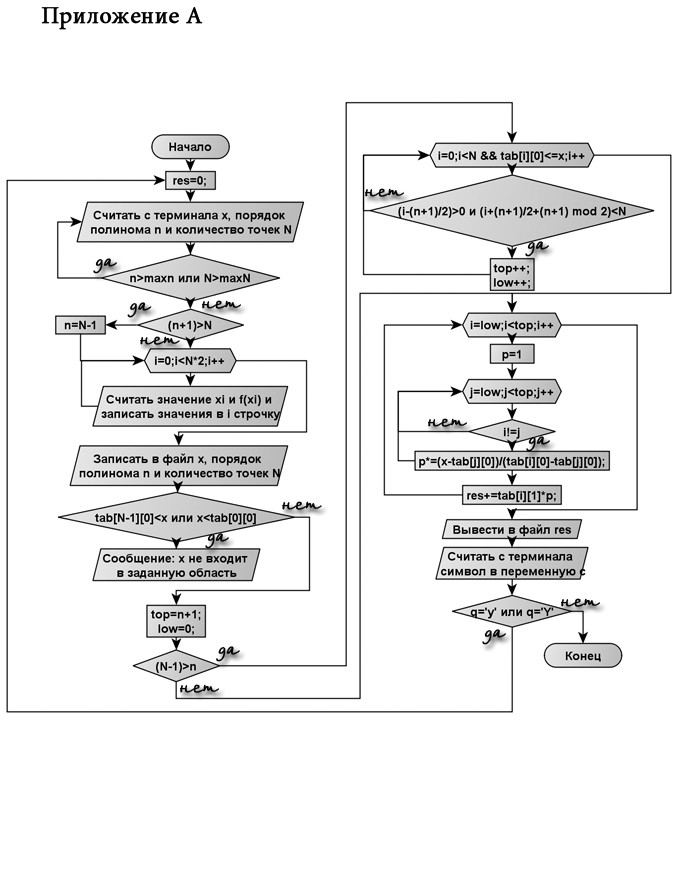Приложение В

#include <stdio.h>

#define maxN 120

#define maxn 9

float tab[maxN][2];

void main()

{

FILE *P,*R;

int N,n;

float x;

char q;

R=fopen("FX.txt","w");

do

{

float res=0;

do

{

printf("Input x, order of polynom(m<10) and value of points(n<121)\n");

scanf("%f %d %d",&x,&n,&N);

}

while(n>maxn || N>maxN);

if ((n+1)>N) n=N-1;

P=fopen("Table.txt","r");

for (int i=0;i<N*2;i++)

fscanf(P,"%f",(&tab[0][0]+i));

fclose(P);

fprintf(R,"x=%.2f\nn=%d\nm=%d\n",x,n,N);

if(tab[N-1][0]<x || x<tab[0][0])

{

printf("x isn't in known area\n");

fprintf(R,"x isn't in known area\n\n");

}

else

{

int top=n+1,low=0,i;

if ((N-1)>n)

{

top=n+1;

for(i=0;i<N && tab[i][0]<=x;i++)

if ((i-(n+1)/2)>0 && (i+(n+1)/2+(n+1)%2)<N) {low++; top++;}

}

for (i=low;i<top;i++)

{

float p=1;

for (int j=low;j<top;j++)

if (i!=j)

p*=(x-tab[j][0])/(tab[i][0]-tab[j][0]);

res+=tab[i][1]*p;

}

fprintf(R,"f(x)=%f\n\n",res);

printf("You may check f(x) result in FX.txt file \n");

}

printf("Do you want to repeat interpolation with another values?(Y/N)\n");

scanf(" %c",&q);

}

while(q=='y' || q=='Y');

fclose(R);

}

Приложение С

Вычислим корень из двух. Функция f(x)= . Во

входной файл запишем значения вычисляющиеся,

особенно близкие к двум, вручную:

Входной файл Table.txt:

0 0

1 1

1.96 1.4

2.25 1.5

3 1.73

4 2

9 3

16 4

25 5

36 6

Выходной файл FX.txt:

x=2.00

n=5

m=6

f(x)=1.414099 отличие от реального значения

0.000114

x=2.00

n=6

m=7

f(x)=1.414133 отличие от реального значения

0.00008

x=2.00

n=7

m=8

f(x)=1.414149 отличие от реального значения

0.000064

x=2.00

n=8

m=9

f(x)=1.414157 отличие от реального значения 0.00056

x=2.00

n=9

m=10

f(x)=1.414163 отличие от реального значения 0.00005

x=2.00

n=7

m=10

f(x)=1.414149 отличие от реального значения 0.000064

Вычислим значения sin(x), взяв в качестве точек табличные значения:

Входной файл Table.txt:

-30 -0.5

0 0

30 0.5

45 0.707

60 0.866

90 1

120 0.866

135 0.707

160 0.5

180 0

Выходной файл FX.txt:

x=15.00

n=9

m=10

f(x)=0.264387 реальное значение:0.258819

x=50.00

n=9

m=10

f(x)=0.766263 реальное значение:0.766044

x=80.00

n=9

m=10

f(x)=0.983149 реальное значение:0.984808

Найдем :

Входной файл Table.txt:

0 0

1 1

2 8

3 27

4 64

5 125

6 216

7 343

8 512

9 729

Выходной файл FX.txt:

x=5.50

n=9

m=10

f(x)=166.375031 реальное значение 166.375

x=4.10

n=9

m=10

f(x)=68.920990 реальное значение 68.921

11