• Упругий удар

До сих пор мы рассматривали только неупругие удары двух тел на примере их наиболее ярких представителей: абсолютно неупругих ударов. Как уже отмечалось ранее, здесь достаточно только одного закона сохранения импульса. Теперь обратимся к упругому удару. Сначала дадим определение: центральным называется удар, при котором все соударяющиеся тела и до, и после удара движутся вдоль одной прямой.

Известны массы m₁ и m₂ материальных точек, испытывающих упругий центральный удар друг с другом. Известны их налетающие скорости: ₁ и ₂. Определить скорости разлёта u₁ и u₂ материальных точек.

Нарисуем механические состояния непосредственно до и сразу после удара.

Запишем закон сохранения импульса при ударе:

.

Возьмём проекцию на направление движения:

.

Мы получили одно уравнение с двумя неизвестными. Значит, один только закон сохранения импульса не позволит решить эту задачу. Такая ситуация возникает всегда, когда два тела после удара по-прежнему двигаются по отдельности. Но в нашем случае есть одно условие, которое позволит без проблем написать второе уравнение. Это упругость удара. Значит, кинетическая энергия тел при ударе сохраняется, следовательно,

.

После подстановки получаем уравнение:

.

Оно вместе с уравнением сохранения импульса составляют замкнутую систему для определения u₁ и и₂:

Эта система плохо поддаётся «стандартному» решению методом подстановки, но существует хорошо известный способ обойти основные трудности, который лучше всего выучить наизусть. Для этого разобьем решение на шаги.

Шаг 1. Группируем члены обоих уравнений по индексам:

Шаг 2. Выносим общие множители:

Шаг 3. Раскладываем разности квадратов:

Шаг 4. Делим почленно первое уравнение на второе (мы имеем право это делать без опаски, т.к. мы делим на массы и разности проекций, которые при ударе должны быть разными):

.

В результате мы получаем очень простое уравнение взамен сложного квадратного уравнения закона сохранения энергии. То есть, можно записать систему, эквивалентную исходной, но гораздо более простую:

Её легко решить методом подстановки:

Вынесем общий множитель в левой части и для дальнейших целей сгруппируем члены правой части по скоростям:

.

Отсюда окончательно:

.

Для того чтобы получить выражение u₂, мы не будем подставлять выражение u₁ в u₂. Вместо этого посмотрим на исходную систему уравнений:

У неё есть одна особенность: перестановка индексов (т.е. замена индекса «1» на индекс «2» и наоборот) приведёт к той же самой системе. Как говорят, система симметрична по отношению к перестановке. В этом случае перестановка индексов в правильном ответе тоже приводит к правильному ответу. Тогда на основании выражения для u₁ получаем выражение для u₂:

; .

• Частица и поверхность

Под взаимодействием частицы и поверхности мы будем понимать удар частицы о поверхность, а поверхность всегда будет принадлежать телу, чья масса М значительно больше массы частицы т. Поверхность мы всегда будем рассматривать гладкую, т.е. без шероховатостей, рёбер, прорезов, острий и проколов. Дело в том, что к гладкой поверхности любой формы всегда можно приблизиться так близко, что она будет казаться бесконечной плоскостью.

В состояниях, необходимых для описания удара, должны совпадать положения, поэтому частицу нужно изображать на поверхности, т.е. на плоскости. В месте падения частицы проведём перпендикуляр к поверхности. Острый угол между скоростью падающей частицы и перпендикуляром к поверхности в точке падения называется углом падения (). Острый угол между скоростью падающей частицы и поверхностью называется углом скольжения (). Угол падения и угол скольжения связаны естественным соотношением:

+=90º,

следовательно, cos=sin.

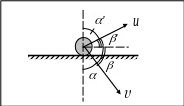
Угол падения очень часто будет появляться в формулах данного пункта, и очень важно не путать его с углом скольжения, потому что это приведёт к ошибке для всех значений угла , кроме 45º.

Нам нужно дать ещё два определения. Острый угол между скоростью отскока и перпендикуляром к поверхности в точке падения называется углом отражения ('). Острый угол между скоростью отскока и поверхностью называется углом скольжения на отскоке (').

'+'=90º; cos'=sin'.

В данном параграфе будут рассматриваться удары только двух типов: упругие и абсолютно неупругие. Начнём с упругого удара.

В этом случае оба необходимых механических состояния можно изобразить «в одном месте». Скорости и , направленные в разные стороны, ясно указывают, какое состояние каждая из них представляет. Для того чтобы понять, чем упругий удар отличается от просто неупругого, достаточно сравнить удар о стену или пол, произведённый хорошо надутым мячом, с ударом плохо надутого мяча. Только удар должен быть простой, т.е. нерезаный и некручёный.

Из упругости удара следует, что ; ; . Следовательно, , т.е. модули скоростей до удара и после совпадают. А как соотносятся направления и ? Очень часто на этот вопрос автоматически дают ответ: «угол падения равен углу отражения». А почему? Как правило, членораздельных объяснений услышать не удаётся. Подчеркнём, что упругость удара сама по себе «отвечает» только за равенство модулей  и u. Но это условие может выполняться при любом соотношении углов падения и отражения.

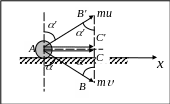
Докажем, что равенство углов падения и отражения достигается при упругом ударе о гладкую поверхность. При этом, как уже показывалось ранее, изменение касательной составляющей импульса частицы равно 0. Следовательно, . Тогда прямоугольные треугольники импульсов АВС и АВ'С' равны по катету и гипотенузе. А в равных треугольниках против равных сторон лежат равные углы. Поэтому угол падения равен углу отражения при упругом ударе только о гладкую поверхность.

С другой стороны, если опытным путём устанавливается (например, при игре в теннис во время приёма простой подачи), что  и ' равны, то поверхность по отношению к этому упругому удару можно считать гладкой. Мы в дальнейшем будем рассматривать упругий удар только о гладкую поверхность (по умолчанию).

Рассмотрим абсолютно неупругий удар частицы о поверхность при произвольном угле падения. Здесь на одном рисунке оба требуемых состояния не уместить.

Импульс системы «частица-поверхность» в первом состоянии

.

А во втором? Если считать, что , то получим, что импульс системы при ударе не сохраняется. Значит, мы не имеем права считать, что поверхность, т.е. тяжёлое тело М, которому она принадлежит, неподвижно во втором состоянии. Пусть его скорость после удара равна . Тогда

.

Следовательно,

.

Если поверхность  асфальтовый плац, то тяжёлое тело  Земля. Пусть лёгкое тело  это капля дождя. Значит, речь идёт о скорости, которую приобретает планета Земля, после того как в неё попадёт капля. Только вдумайтесь! Имеет ли смысл учитывать эту скорость? Если Вы действительно представили ситуацию, то известно, какой ответ у Вас напрашивается. Но правильный ответ: «да, имеет». Если пренебречь скоростью и, то не выполнится закон сохранения импульса при ударе, а этот закон гораздо важнее того, что подсказывает здравый смысл. Нечеловечески маленькая скорость u умножается на нечеловечески большую массу М, и получается «человеческий» импульс m. В результате удара тело, обладающее поверхностью, или коротко, поверхность приобретает импульс, сопоставимый с импульсом налетающего тела. А если и=0, то какая бы большая ни была масса М, произведение её на 0 будет равно 0.

Как измерить передачу импульса поверхности со стороны частицы? Совершенно очевидно, что «прямое измерение» ни к чему не приведёт, поскольку скорость, приобретаемую Землёй в результате удара о неё капли или мяча, никакими приборами определить невозможно. Гораздо проще исходить из закона сохранения импульса системы «частица-поверхность» при ударе:



Как ни странно, эта простая формула и есть главная формула данного пункта: