
Геометрия метод координат
Пусть на (i,
j,
k)
заданы
![]() ,
тогда операции над ними будут равны:
,
тогда операции над ними будут равны:
![]()
![]() ;
;
![]()
![]()
![]()
![]()
![]() Пусть A
( x1;
y1;
z1);
B
(x2;
y2;
z2);
тогда:
Пусть A
( x1;
y1;
z1);
B
(x2;
y2;
z2);
тогда:
вектор![]() ;
модуль вектора
;
модуль вектора![]()
Треугольник
в нешний
угол СВД
=
нешний
угол СВД
=
![]() ;
К – точка пересечения высот (ортоцентр
треугольника). ha,
hb,
hc
– высоты треугольника на соответствующие
стороны.
;
К – точка пересечения высот (ортоцентр
треугольника). ha,
hb,
hc
– высоты треугольника на соответствующие
стороны.
![]() где полупериметр
где полупериметр
![]() .
.
М – точка пересечения медиан треугольника (центр тяжести).
m a,
mb,
mc
– медианы на соответствующие стороны.
МВ:МД=МА:МЕ=МС:МК=2/1
a,
mb,
mc
– медианы на соответствующие стороны.
МВ:МД=МА:МЕ=МС:МК=2/1
![]()
Т – точка пересечения биссектрис треугольника (центр вписанной окружности). La, Lb, Lc – биссектрисы соответствующих углов. ВМ:МС = АВ:АС
![]()
![]()
r
– радиус вписанной окружности. О –
точка пересечения серединных
перпендикуляров к сторонам треугольника
(центр описанной окружности). Радиус
описанной окружности:


![]() где
SΔ
– площадь треугольника; p
– периметр треугольника; hc
–
где
SΔ
– площадь треугольника; p
– периметр треугольника; hc
–
высота опущенная на соответствующую сторону с. На всех 4–х нарисованных треугольниках стороны одинаково обозначены, просто на 1–м они обозначены, а на остальных они опущены для упрощения рисунка. И вообще подразумевается, что все 4 треугольника абсолютно одинаковые.
M N
– средняя линяя треугольника. MN=0.5AC;
MN║AC.
N
– средняя линяя треугольника. MN=0.5AC;
MN║AC.
ТЕОРЕМА СИНУСОВ
![]() где R
– радиус описанной окружности.
где R
– радиус описанной окружности.
![]()
ТЕОРЕМА КОСИНУСОВ
![]()
![]()
![]()
![]()
![]()
![]()
ПЛОЩАДЬ ТРЕУГОЛЬНИКА
![]() где
где
![]() –
длины сторон
треугольника, а
–
длины сторон
треугольника, а
![]() –
высоты, опущенные
на соответствующие стороны.
–
высоты, опущенные
на соответствующие стороны.
![]()
![]()
![]()
![]() – формула Герона.
– формула Герона.
РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК
![]() тогда площадь
тогда площадь
![]()

ПРАВИЛЬНЫЙ ТРЕУГОЛЬНИК
![]()
![]()
![]()
![]()
ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
а и b – катеты, с – гипотенуза, ас и bc – проекции катетов на гипотенузу.
а2 + b2 = c2 – теорема Пифагора.
S=
a·b/2
= c·hc/2;
![]() – радиус вписанной окружности.
– радиус вписанной окружности.
R
= c/2,
– радиус описанной окружности.
![]()
sinA = a/c; cosA = b/c; tgA = a/b; ctgA = b/a; b2 = c·bc;
a = c·sinA = c·cosB = b·tgA = b·ctgB; c = a/sinA = a/cosB = 2R;
ПАРАЛЛЕЛОГРАММ
![]()
![]()
![]()
![]()

ПРЯМОУГОЛЬНИК
![]()
РОМБ
![]()
КВАДРАТ
![]()

ТРАПЕЦИЯ
а и b – основания, h – высота
![]()
ОКРУЖНОСТЬ И КРУГ
Длина окружности с =2πR. Площадь круга S = πR2 = πD2/4.
Длина дуги l = π·R·α/1800. Площадь сектора S = π·R2·α/3600.
где α – величина угла дуги в градусах.
ЧЕТЫРЁХУГОЛЬНИК И КРУГ
Свойство вписанного четырёхугольника:
ac + bd = ef, где a,b,c,d – стороны, e,f – диагонали.
Свойство описанного четырехугольника: a + c = b + d;
S = p·r, p – полупериметр.
ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ
Внутренний угол
![]() где
n
– число сторон. an
= 2R·sin(1800/n);
где
n
– число сторон. an
= 2R·sin(1800/n);
Sn = ½ ·n·an·r; Sn = ½ ·Pn·r; r = R·cos(1800/n);
ШЕСТИУГОЛЬНИК
![]()
СТЕРЕОМЕТРИЯ
ПРИЗМА
Боковая поверхность наклонной призмы Sб.п. = P1·l, где P1 – периметр перпендикулярного сечения, l – ребро призмы.
Боковая поверхность прямой призмы Sб.п. = Pосн ·l; Объём призмы Vпр=Sосн·h;
ПИРАМИДА
I


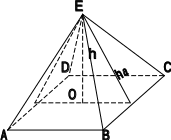 .
Если боковые рёбра
пирамиды равнонаклонены к плоскости
основания (их длины равны), то высота
проходит через центр окружности описанной
около многоугольника основания.
.
Если боковые рёбра
пирамиды равнонаклонены к плоскости
основания (их длины равны), то высота
проходит через центр окружности описанной
около многоугольника основания.
II. Если боковые грани пирамиды равнонаклонены к плоскости основания (длины апофемы равны), то высота проходит через центр окружности, вписанной в многоугольник основания.
Площадь боковой поверхности правильной пирамиды: Sб.пир.= ½ ·Pосн·ha , где ha – апофема.
Sб.пир.= Sосн /cosα , где α – угол наклона боковой грани к основанию.
Объём пирамиды: Vпир= ⅓·Sосн·h, где h – высота пирамиды.
Площадь боковой поверхности правильной усечённой пирамиды: Sбок= ½ ·(P1+P2)·ha , где P1, P2 – периметры оснований (верхнего и нижнего); ha – апофема.
Объём усечённой
пирамиды:
![]() где
Q1
и Q2
– площади оснований.
где
Q1
и Q2
– площади оснований.
ТЕЛА ВРАЩЕНИЯ
ЦИЛИНДР
Площадь боковой поверхности: Sбок =2·π·R·h. Площадь всей пов–ти: S=2·π·R·(R + h). Объём: V = πR2·h;
КОНУС
Площадь пов–ти конуса: боковой Sб=πrl; полной Sп=πr ·(r + l); где l – образующая. Объём: V=πr2h/3;
УСЕЧЁННЫЙ КОНУС
Площадь боковой пов–ти: Sб.у.к.= π·l·(R + r); Объём: V=⅓·π·h(R2 + r2 +Rr); угол развёртки: α=(R–r)/l;
ШАР
Площадь пов–ти сферы: Sсф=4πR2; Объём шара: Vш=4/3·πR 3
