MET-ЧМ-Часть-2

УДК 621.313: 518.6 ББК 32.81

А95 Методические указания к лабораторным и самостоятельным работам по курсам «Информатика» и «Вычислительная математика». Численные мето- ды. Часть 2. / Казанский государственный архитектурно-строительный уни- верситет. Сост.: Ф.Г.Ахмадиев, Ф.Г.Габбасов, Р.Ф.Гиззятов, И.В.Маланичев.

Казань, 2011. – 36 с.

Печатается по решению Редакционно-издательского совета Казанского государственного архитектурно-строительного университета.

Методические указания состоят из двух частей и предназначены для выполнения лабораторных и самостоятельных работ студентами всех специ- альностей и направлений подготовки дневного и заочного отделений. В дан- ной части приводятся численные методы аппроксимации функций, вычисле- ния определенных интегралов, решения дифференциальных уравнений и за- дач линейного программирования.

Рецензент Доктор физико-математических наук, профессор КГАСУ

Р.Б.Салимов

УДК 621.313: 518.6 ББК 32.81

ã Казанский государственный архитектурно-строительный университет, 2011

ã Ахмадиев Ф.Г., Габбасов Ф.Г., Гиззятов Р.Ф., Маланичев И.В., 2011

3

4.Аппроксимация функций.

4.1.Приближение функции по методу наименьших квадратов (МНК).

Очень часто в практической работе возникает необходимость найти в

явном виде функциональную зависимость между величинами x и y , кото- рые получены в результате измерений.

Как правило, общий вид этой функциональной зависимости или так на- зываемой «эмпирической формулы» известен, а некоторые числовые пара- метры закона неизвестны.

Процесс выражения опытных данных функциональной зависимостью с помощью метода наименьших квадратов состоит из двух этапов: на первом этапе выбирают вид искомой формулы, а на втором этапе для формулы под- бирают параметры. Для первого этапа удобно графическое представление за- висимости, на втором этапе, в соответствии с идеей МНК, необходимо ми- нимизировать сумму отклонений:

где xi , yi - значения опытных данных y(xi ) - значение функции, вычислен- ное в точке xi ; n - число данных.

Линейная аппроксимация. В случае линейной эмпирической форму- лы y(x) = ax + b и (4.1) принимает вид:

n

S(a,b) = å(ax + b − yi )2 → min (4.2)

i=1

Функция (4.2) имеет минимум в точках, в которых частные производ- ные от S по параметрам a и b обращаются в нуль, т.е.

4

Решая систему уравнений (4.4), получим значения a и b уравнения y(x) = ax + b .

Пример 4.1. Подобрать аппроксимирующий полином первой степени y(x) = ax + b для данных

Решение. Для удобства вычисленные значения расположим в таблице.

Система для определения коэффициентов имеет вид:

ì21a + 7b = 20,1

ï

íï7a + 4b = 6,9 (4.5)

î

Решая систему (4.5), получим следующие значения параметров:

a = 0,917 , b = 0,120. Следовательно, искомый полином имеет вид: y(x) = 0,917x + 0,120.

Полиномиальная аппроксимация. В случае выбора зависимости в виде полинома, например, 2-й степени y~(x) = ax2 + bx + c и (4.1) принимает вид:

n

S(a,b,c) = å(ax2 + bx + c - yi )2 ® min (4.6)

i =1

Функция (4.6) имеет минимум в точках, в которых частные производ- ные от S по параметрам a , b , c обращаются в нуль, т.е.:

В результате дифференцирования и элементарных преобразований для определения параметров получают систему из трех линейных уравнений с тремя неизвестными:

5

Решая систему линейных уравнений (4.8), получим значения a , b и c уравнения y~(x) = ax2 + bx + c .

Пример 4.2. Используя МНК, построить эмпирическую зависимость y~(x) = ax2 + bx + c , аппроксимирующую следующие табличные значения:

Решение. Расчеты представим в виде таблицы.

Таблица 4.4.

Тогда система линейных уравнений (4.8) относительно значений a , b и c примет вид:

ï10a + 0b + 5c = 4

î

6

Решая систему (4.9), получим следующие значения параметров a = 0,857 ;b = −1,800; c = −0,914 . Таким образом, искомый полином имеет

Пример 4.3. Используя программу Excel, построить эмпирическую за- висимость вида y~(x) = ax2 + bx + c , аппроксимирующую значения из таб- лицы 4.3:

Порядок решения.

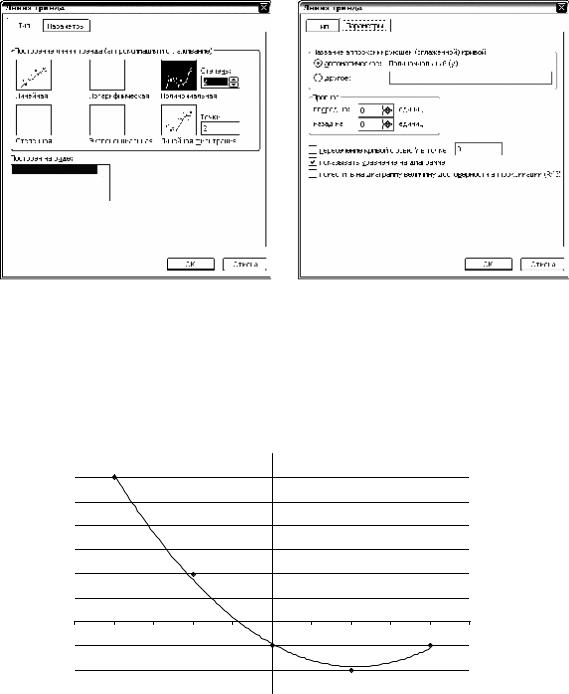
1)Ввести таблицу в рабочий лист Excel (рис. 4.1). Выделить ячейки таб- лицы.

2)Вызвать Мастер диаграмм. Выбрать тип диаграммы – точечная (без соединительных линий). Нажать кнопку «Готово». На рабочем листе появится график точек таблицы.

Рис. 4.1. Добавление линии тренда в точечную диаграмму.

7

3)Вызвать контекстное меню (правой кнопкой мыши) одной из точек графика. Выбрать пункт «добавить линию тренда».

4)На вкладке тип выбрать полиномиальная аппроксимация и устано- вить степень полинома, равной 2 (рис. 4.2).

5)На вкладке параметры отметить «показывать уравнение на диаграмме».

Рис. 4.2. Настройка параметров линии тренда.

6)Закрыть окно настроек, нажав кнопку ОК. Появляется линия графика аппроксимирующей функции и соответствующая формула (рис. 4.3):

y(x) = 0,8571x2 − 1,8x − 0,9143

y = 0,8571x2 - 1,8x - 0,9143

Рис. 4.3. Результаты аппроксимации.

8

Аппроксимация линеаризацией. Многие нелинейные функции, зави- сящие от двух параметров, можно линеаризовать путем замены переменных. Для этого необходимо подобрать такое преобразование исходной зависимо- сти y(x) = ϕ(x,a,b), в результате которого она приобретает линейный вид Y = AX + B . Далее решается задача линейной аппроксимации для новой за- висимости, и вычисленные коэффициенты A и B пересчитываются в a и b .

Пример 4.4. Используя МНК, построить эмпирическую зависимость y~(x) = bxa , аппроксимирующую следующие табличные значения:

Решение. Расчеты представим в виде таблицы.

Система для определения коэффициентов имеет вид:

9

Аппроксимация произвольной функцией может быть выполнена в программе Excel с помощью модуля «Поиск решения».

Пример 4.5. Используя программу Excel, построить эмпирическую за- висимость, аппроксимирующую значения из таблицы:

Таблица 4.9.

Порядок решения.

1)Аппроксимирующая функция должна иметь экстремум в виде пика. Выберем следующую функцию, зависящую от трех параметров ai :

3)В ячейки A5:A11 – значения xi

4)В ячейки B5:B11 – значения yi

5)В ячейку C5 – формулу аппроксимирующей функции (на ячейки с па-

раметрами абсолютные ссылки): =$A$2*EXP(-((A5-$B$2)^2)/$C$2)

6)Скопировать формулу в ячейки C6:C11

11)Нажать кнопку Выполнить.

12)Подтвердить сохранение найденного решения.

13)Рабочий лист изменился и содержит решение (рис. 4.4):

a1 = 1,81559 a2 = 2,450734 a3 = 0,968182

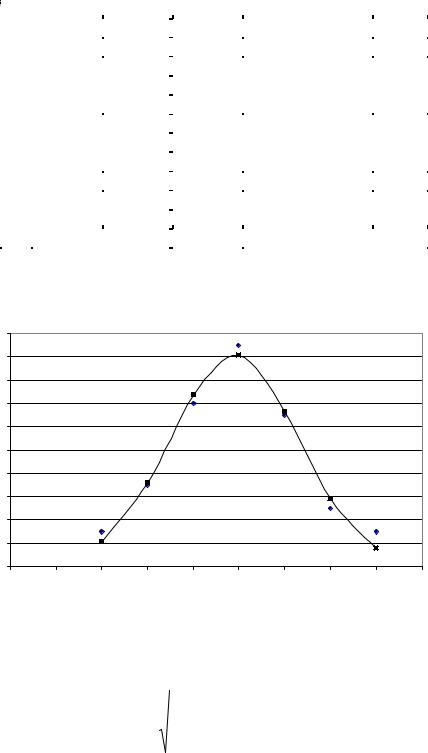
10

Таким образом, аппроксимирующая данные табл. 4.9 функция имеет

вид:

Рис. 4.4. Аппроксимация данных нелинейной функцией с тремя параметрами с помощью программы Excel.

Рис. 4.5. Результаты аппроксимации функцией с тремя параметрами.

Точность аппроксимации можно оценить среднеквадратической ошибкой

которая не должна превышать погрешность исходных данных.