
- •Запишите формулы для математического ожидания и дисперсии выборочной доли в случае повторной (бесповторной) выборки. Поясните все используемые обозначения.
- •Сформулируйте определение выборки из распределения. Как в этом случае определяются: выборочное среднее, выборочные начальные и центральные моменты, выборочная функция распределения?
- •Докажите формулы для математического ожидания и дисперсии выборочного среднего в случае повторной выборки.
- •Выведите формулу для дисперсии выборочного среднего бесповторной выборки.
- •Что такое точечная статистическая оценка? Какие оценки называются несмещенными, эффективными, состоятельными? Приведите пример эффективной оценки.
- •Запишите формулу для несмещенной оценки начального момента произвольного порядка. Докажите несмещенность.
- •Сформулируйте теорему Слуцкого и на ее основе докажите теорему о состоятельных оценках центральных моментов.
- •Сформулируйте определения распределений χ², Стьюдента и Фишера. Какие из этих распределений являются симметричными?
- •Что называется интервальной оценкой параметра распределения? Какие оценки называются симметричными по вероятности? Определите понятия: доверительная вероятность и точность оценки.
- •Пояснив используемые символы, запишите (1–α)-доверительный интервал (симметричный по вероятности) для дисперсии при известном математическом ожидании. В каких случаях применима данная формула?
- •Пояснив используемые символы, запишите (1–α)-доверительный интервал (симметричный по вероятности) для дисперсии при неизвестном математическом ожидании. В каких случаях применима данная формула?
- •Запишите приближенный (1–α)-доверительный интервал для генеральной доли признака в случае выборки большого объема n (n→∞). Поясните все используемые символы.
- •Пояснив используемые символы, запишите (1–α)-доверительный (симметричный по вероятности) интервал предсказания. Для каких генеральных распределений применима данная формула?
- •Опишите общую схему проверки статистических гипотез. Определите понятия: критическая область, уровень значимости, мощность критерия. Какие гипотезы называются простыми (сложными)?
- •Определите отношение правдоподобия для дискретных и абсолютно непрерывных распределений. Сформулируйте теорему (лемму) Неймана – Пирсона и приведите пример наиболее мощного критерия.
- •Определите p-значение статистического критерия. Каким образом находится p-значение, если известно распределение статистики критерия ? Рассмотрите случай критической области вида
- •В чем состоит метод наименьших квадратов (мнк)? Используя матричную запись, укажите явный вид (приближенного) решения системы линейных уравнений по мнк. В каком случае мнк-решение не существует?
Определите отношение правдоподобия для дискретных и абсолютно непрерывных распределений. Сформулируйте теорему (лемму) Неймана – Пирсона и приведите пример наиболее мощного критерия.
Пусть генеральное
распределение имеет строго положительная
плотность
![]() ,зависящую
от параметра тетта.
,зависящую
от параметра тетта.
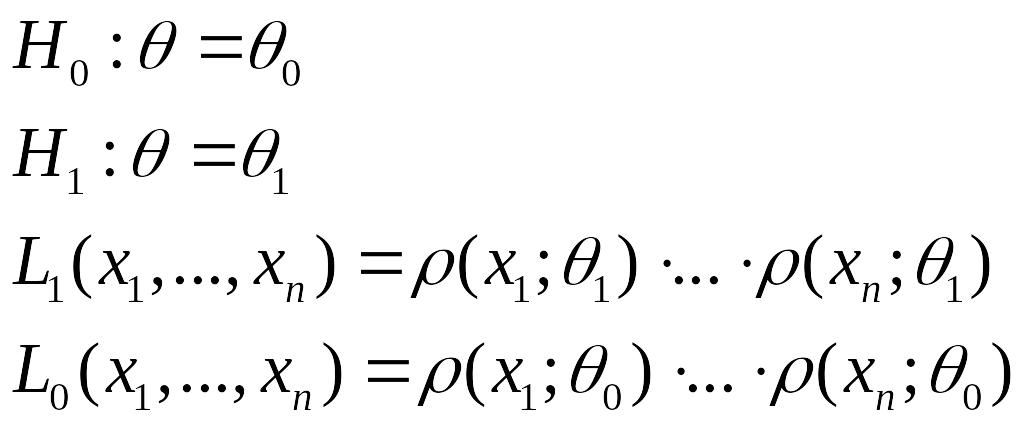
L0, L1- функции правдоподобия.
отношением правдоподобия называется отношение
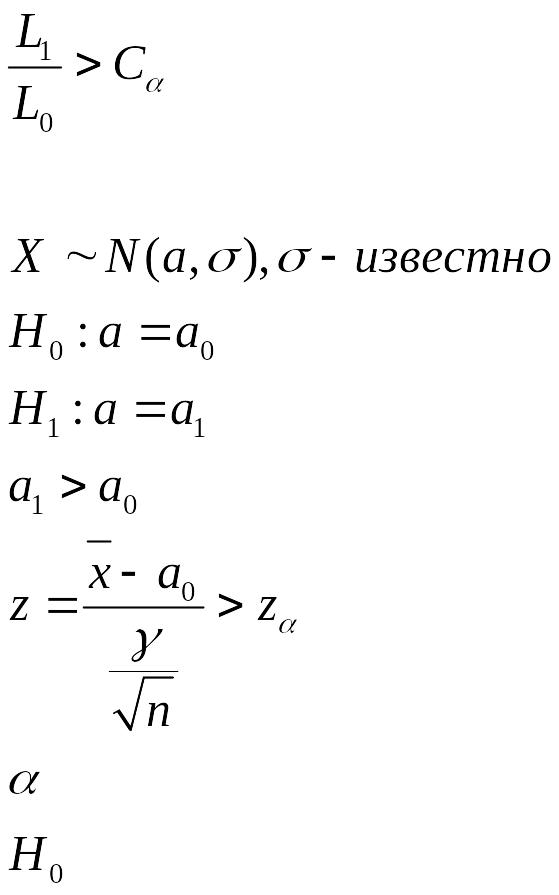
Лемма Немана-Пирсона:
Для любого уровня значимости
существует такая константа
![]() ,
что критерия с критической областью:
,
что критерия с критической областью:
![]() является наиболее
мощным критерием среди всех статистических
критериев с какой-либо критической
областью К по проверке статистической
гипотезы
является наиболее
мощным критерием среди всех статистических
критериев с какой-либо критической
областью К по проверке статистической
гипотезы
![]() против гипотезы
против гипотезы
![]()
Пример наиболее мощного критерия:
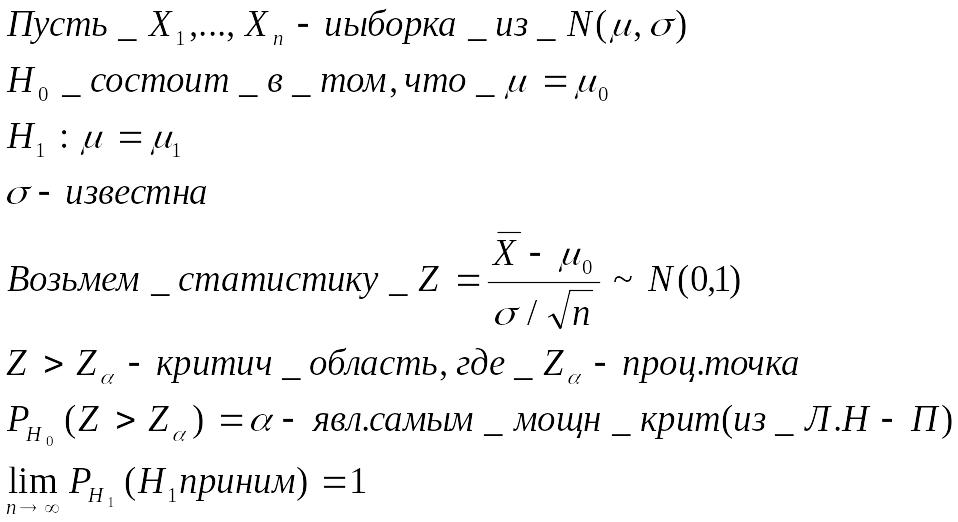
Какие статистические критерии называются критериями согласия? Сформулируйте общую схему по проверке гипотезы о вероятностях событий, образующих полную группу, по критерию Пирсона без оценки неизвестных параметров.
Критерий согласия предназначен для проверки согласованности основной гипотезы Н0 с выборочными данными, однако, в отличии от других критериев, альтернативная гипотеза явным образом не выдвигается.
Производится серия повторных независимых испытаний, wt- элементарный исход испытания с номером t.
Пусть А1,…,Аl – образуют полную группу событий. Исходными данными для критерия хи-квадрат Пирсона является таблица эмпирических частот
Событие |
А1 |
… |
Al |
частота |
|
… |
n |
Если
основная гипотеза верна, согласно
статистическому определению вероятности
![]() -относительная
частота события Аi.
В качестве меры одновременной близости
l
пар чисел (
-относительная
частота события Аi.
В качестве меры одновременной близости
l
пар чисел (![]() )
можно принять любую сумму вида
)
можно принять любую сумму вида
![]() ,
в которой ci>0
какие –либо положительные числа. Пирсон
обнаружил, что если придать большие вес
маловероятным событиям, положив
,
в которой ci>0
какие –либо положительные числа. Пирсон
обнаружил, что если придать большие вес
маловероятным событиям, положив
![]() ,
то при неограниченном увеличении n
распределение статистики
,
то при неограниченном увеличении n
распределение статистики
![]()
Перестает зависеть от конкретных значений вероятностей pi и стремится к распределению хи квадрат с l-1 степенями свободы.
Заметим, что при верной Но, случайные величины ni распределены по биноминальному закону с параметрами n и pi, вследствие чего npi=Е(ni) называется ожидаемой (теоретической) частотой события Аi.теоретические частоты, ni- кол-во элементарных исходов в группе, l- кол-во групп, pi-заданная вероятность.
Найдем асимптотическое ( при n стремящемся к бесконечности)распределение статистики хи квадрат. Рассмотрим с этой целью l-мерный вектор
![]()
Этот
вектор имеет единичную длину, вследствие
чего может быть дополнен до ортонормированного
базиса
![]() ,…,
,…,![]() в
Rl.
в
Rl.
Определим l величин:
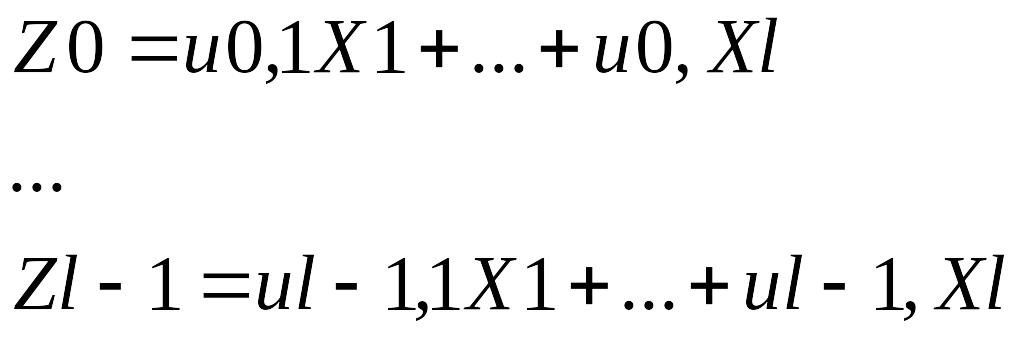
Где uk,i- i-ая компонента вектора uk, а Xi определяется соотношением
![]()
Из
этого следует, что
![]() ,
а из ортонормированности базиса
,…,
вытекает,что
суммы квадратов Х1,…,Хl
и Z0,…,Zl-1
совпадают
,
а из ортонормированности базиса
,…,
вытекает,что
суммы квадратов Х1,…,Хl
и Z0,…,Zl-1
совпадают
Нетрудно видеть, что
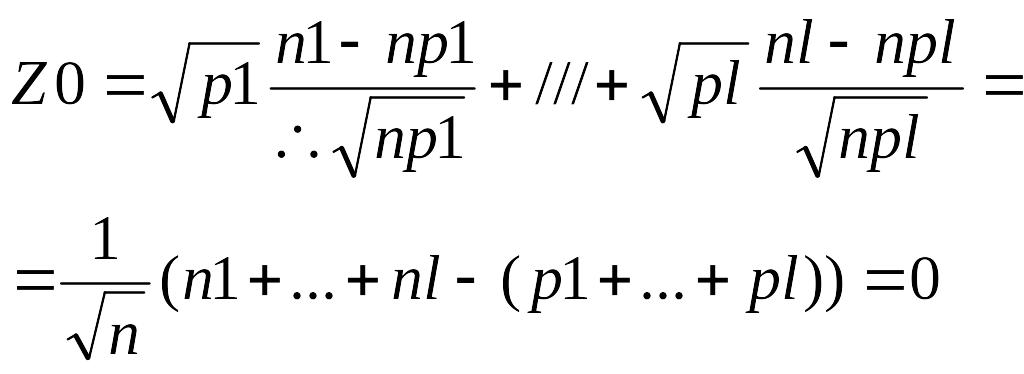
Получаем
![]()
Случайный вектор Z имеет нулевое математическое ожидание и единичную ковариационную матрицу. Применяя многомерный аналог центральной предельной теоремы, можно доказать, что при n стремящемся к бесконечности распределение вектора Z стремится к l-1-мерному нормальному распределению. В итоге получаем, что распределение статистики при достаточно большом n близко к распределению хи квадрат с l-1 степенями свободы.
Можно также доказать,
что если гипотеза H0
не верна, то при n
стрем. к бесконечности вероятность
![]() для
любого с, что в конечном счете определяет
достаточно высокую мощность критерия
Пирсона.
для
любого с, что в конечном счете определяет
достаточно высокую мощность критерия
Пирсона.
В итоге приходим к
выводу, что проверки по эмпирическим
данным справедливости распределения
с асимптотическим уровнем значимости
альфа можно использовать критерий
согласия хи квадрат Пирсона и критической
областью
![]() .
.
Сформулируйте общую схему статистической проверки гипотезы о виде распределения по критерию Пирсона с оценкой неизвестных параметров. Как частный случай опишите проверку гипотезы о нормальном распределении.
Часто встречаются
ситуации, когда гипотетическая
вероятностная мера Р зависит от одного
или нескольких параметров
![]() ,
,
Р(А)=Р(А;
![]() ),
),
Что приводит к зависимости вероятностей pi от :
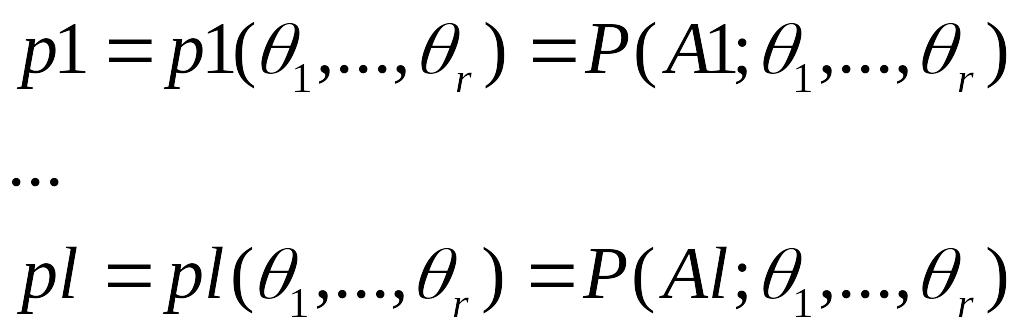
Проверяемая( возможно непараметрическая) гипотеза Н часто формулируется как утверждение о том, что истинная вероятностная мера Pист совпадает с гипотетической мерой Р при определенных значениях параметров . Тем не менее, фактической проверке подвергается не Н, а вытекающая из Н гипотеза Н0 о том, что распределение частот согласуется с распределением при определенном наборе значений параметров . Заметим, что при любой Н гипотеза Н0 заведомо является параметрической гипотезой поскольку распределение определяется конечным числом параметров.
Сложности гипотезы
Н0 приводит к необходимости предварительной
оценки параметров
тем или иным способом. Предположим, что
![]() -оценки,
полученные методом максимального
правдоподбия по таблице эмпирических
частот
-оценки,
полученные методом максимального
правдоподбия по таблице эмпирических
частот
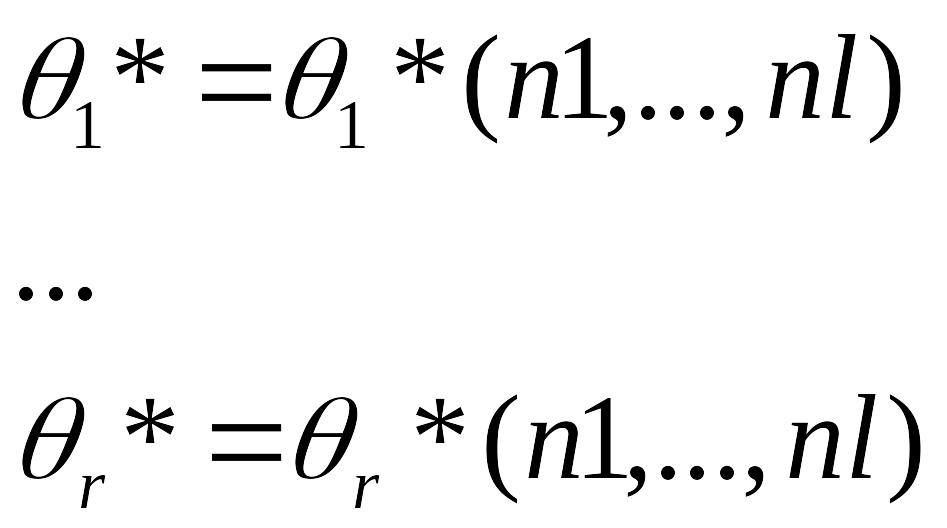
Заменив в вероятность рi на их оценки
![]() получим
статистику вида
получим
статистику вида
![]()
Произведение np*i по прежнему интерпретируется как ожидаемая частота события Аi , несмотря на то, что np*i – случайная величина ( в отличие от npi)
Оказывается, что при выполнении некоторых достаточно общих условий распределение статистики при n стремящемся к бесконечности стремится к распределения хи квадрат с l-r-1 степенями свободы, в котором число степеней свободы по сравнению с аналогичным предельным распределением уменьшилось на количество оцененных параметров.
Сформулируйте общую схему статистической проверки гипотезы о виде распределения по критерию Пирсона с оценкой неизвестных параметров. Как частный случай опишите проверку гипотезы о нормальном распределении.
Часто встречаются ситуации, когда гипотетическая вероятностная мера Р зависит от одного или нескольких параметров ,
Р(А)=Р(А; ),
Что приводит к зависимости вероятностей pi от :
Проверяемая( возможно непараметрическая) гипотеза Н часто формулируется как утверждение о том, что истинная вероятностная мера Pист совпадает с гипотетической мерой Р при определенных значениях параметров . Тем не менее, фактической проверке подвергается не Н, а вытекающая из Н гипотеза Н0 о том, что распределение частот согласуется с распределением при определенном наборе значений параметров . Заметим, что при любой Н гипотеза Н0 заведомо является параметрической гипотезой поскольку распределение определяется конечным числом параметров.
Сложности гипотезы Н0 приводит к необходимости предварительной оценки параметров тем или иным способом. Предположим, что -оценки, полученные методом максимального правдоподбия по таблице эмпирических частот
Заменив в вероятность рi на их оценки
получим статистику вида
Произведение np*i по прежнему интерпретируется как ожидаемая частота события Аi , несмотря на то, что np*i – случайная величина ( в отличие от npi)
Оказывается, что при выполнении некоторых достаточно общих условий распределение статистики при n стремящемся к бесконечности стремится к распределения хи квадрат с l-r-1 степенями свободы, в котором число степеней свободы по сравнению с аналогичным предельным распределением уменьшилось на количество оцененных параметров.
Какие выборки называются однородными? Сформулируйте критерий Колмогорова – Смирнова по проверке с заданным уровнем значимости α гипотезы об однородности двух выборок. Каким образом находится значение статистики данного критерия?
Пусть
![]() - выборка из распределения Li
объема ni,
где i=1,…,k.
Независимые выборки из одного и того
же распределения L1=…=Lk,
называются однородными.
- выборка из распределения Li
объема ni,
где i=1,…,k.
Независимые выборки из одного и того
же распределения L1=…=Lk,
называются однородными.
Для проверки однородности нескольких выборок для двух выборок можно применить критерий Колмогорова-Смирнова. Схема его применения довольно похожа на схему применения критерия Колмогорова, но в данном случае мы сравниваем не эмпирическую функцию распределения и теоретическую, а две эмпирические.
Итак, предположим,
что у нас есть две выборки. Пусть
![]() -выборка
из распределения
-выборка
из распределения
![]() объема m и
объема m и
![]() -выборка
из распределения
-выборка
из распределения
![]() объема n. Независимые выборки
объема n. Независимые выборки
![]() полученные из одного и того же распределения
полученные из одного и того же распределения
![]() называются однородными. Пусть
называются однородными. Пусть
![]() -реализация
-реализация
![]() и
и
![]() -реализация
-реализация
![]() .
Эмпирические функции распределения
обозначим
.
Эмпирические функции распределения
обозначим
![]() -
для случайных выборок и
-
для случайных выборок и
![]() -
для из реализаций. Определим расстояние
между функциями
-
для из реализаций. Определим расстояние
между функциями
![]() формулой:
формулой:
![]()
Пусть X –конечное
множество, образованное всеми различными
компонентами выборок
![]() Тогда
Тогда
![]()
Расстояние для
случайных выборок
![]() определяется
аналогично.
определяется
аналогично.
Если предположить,
что выборки
однородны и, кроме того, извлечены из
распределения с непрерывной функцией
![]() .
В таком случае распределение случайной
величины
не зависит от
.
Для доказательства определим случайные
векторы:
.
В таком случае распределение случайной
величины
не зависит от
.
Для доказательства определим случайные
векторы:
![]()
Компоненты векторов
независимы и равномерно распределены
но отрезке от нуля до единицы. Следовательно,
эти вектора можно рассматривать как
выборки объемов m и n из равномерного
распределения на отрезке от нуля до
единицы. Независимость распределения
от
вытекает из того, что
![]()
Процентные точки
![]() распределения
распределения
![]() определяются
соотношением
определяются
соотношением
![]() Для проверки гипотезы однородности
двух выборок, полученных из непрерывных
распределений, применяется критерий
Смирнова, критическая область которого
задается неравенством
Для проверки гипотезы однородности
двух выборок, полученных из непрерывных
распределений, применяется критерий
Смирнова, критическая область которого
задается неравенством
![]() При небольших m и n для нахождения
критических значений используют
справочные материалы. При больших m и n
можно воспользоваться результатом
Смирнова, который доказал, что при
При небольших m и n для нахождения
критических значений используют
справочные материалы. При больших m и n
можно воспользоваться результатом
Смирнова, который доказал, что при
![]() (и
непрерывной
)
(и
непрерывной
)
![]() где
K(u) – функция предельного распределения
Колмогорова. Соответствующий критерий
называется критерием Колмогорова-Смирнова
и задается критической областью
где
K(u) – функция предельного распределения
Колмогорова. Соответствующий критерий
называется критерием Колмогорова-Смирнова
и задается критической областью
![]() где
где
![]()
![]() -
корень уравнения
-
корень уравнения
![]() .
- асимптотический уровень значимости,
т.е. его фактическое значение достигает
лишь в пределе при
.
На практике критерий Колмогорова-Смирнова
применяется, если объем обеих выборок
не меньше 50.
.
- асимптотический уровень значимости,
т.е. его фактическое значение достигает
лишь в пределе при
.
На практике критерий Колмогорова-Смирнова
применяется, если объем обеих выборок
не меньше 50.
Для проверки каких гипотез применяется критерий Колмогорова? Каким образом находится значение статистики данного критерия?
Его применяют для проверки гипотезы о совпадении истинной функции распределения с некоторой гипотетической функцией распределения. В данной работе он будет использован для проверки равномерности распределения Р-значений критериев на отрезке от нуля до единицы.
Итак, для любого
![]() число компонент вектора
число компонент вектора
![]() ,
которые меньше
,
которые меньше![]() ,
обозначим
,
обозначим
![]() .
Для случайного вектора
.
Для случайного вектора
![]() обозначение
обозначение
![]() имеет тот же смысл, но при этом
является дискретной случайной величиной
с возможными значениями 0,1,…,n. Пусть
имеет тот же смысл, но при этом
является дискретной случайной величиной
с возможными значениями 0,1,…,n. Пусть
![]() -реализация случайной выборки
-реализация случайной выборки
![]() объема
n из некоторого распределения с функцией
объема
n из некоторого распределения с функцией
![]() .
Эмпирическую функцию распределения,
соответствующую выборке
.
Эмпирическую функцию распределения,
соответствующую выборке
![]() ,
можно записать в виде
,
можно записать в виде
![]()
Оценка функции по случайной выборке записывается аналогично:
![]()
Заметим, что
![]() -
числовая функция, тогда как
-
числовая функция, тогда как
![]() в
каждой точке
принимает случайное значение, т.е.
является случайным процессом.
в
каждой точке
принимает случайное значение, т.е.
является случайным процессом.
Итак, расстояние
между функциями
![]() (эмпирическая функция) и
(теоретическая
функция) определяется формулой
(эмпирическая функция) и
(теоретическая
функция) определяется формулой
![]()
Для функции
![]() расстояние
расстояние
![]() - это простое число, тогда как для
- это простое число, тогда как для
![]() расстояние
является случайной величиной, принимающей
значения на отрезке [0,1].
расстояние
является случайной величиной, принимающей
значения на отрезке [0,1].
Основанием для
выбора в качестве меры расхождения
величины d является простота ее вычисления.
Вместе с тем, она имеет достаточно
простой закон распределения. А. Н.
Колмогоров доказал, что в случае
непрерывной функции F(x) при любом
неотрицательном
![]() существует предел:
существует предел:
![]() где
где
![]()
Вследствие этого критерий согласия с критической областью
![]() где
-
корень уравнения
,
имеет при
где
-
корень уравнения
,
имеет при
![]() уровень значимости, стремящийся к
.
То есть
- асимптотический уровень значимости.
Именно этот критерий и называется
критерием Колмогорова.
уровень значимости, стремящийся к
.
То есть
- асимптотический уровень значимости.
Именно этот критерий и называется
критерием Колмогорова.
Отметим, что поскольку
при
![]() фактический уровень значимости заметно
отличается от номинального значения
,
то критерий Колмогорова применяется
при
фактический уровень значимости заметно
отличается от номинального значения
,
то критерий Колмогорова применяется
при
![]() .
.
На практике при вычислении максимального абсолютного отклонения теоретической функции от эмпирической функции применяется следующая формула:
 где
где
![]() -i-ый
член вариационного ряда
-i-ый
член вариационного ряда
![]()
Эквивалентность
этой формулы и приведенной ранее
![]() следует
из того, что
–
неубывающая функция, а
принимает постоянное значение на
интервалах:
следует
из того, что
–
неубывающая функция, а
принимает постоянное значение на
интервалах:
![]()
Итак, схема применения
критерия А. Н. Колмогорова следующая:
строятся эмпирическая функция
распределения
и предполагаемая теоретическая функция
распределения
,
определяется
![]() - максимум модуля разности между ними.
Далее определяется величина
- максимум модуля разности между ними.
Далее определяется величина
![]() и по табличным значениям находится
вероятность того, что, если случайная
величина действительно распределена
по закону
,
за счет чисто случайных причин максимальное
расхождение между
и
будет не меньше, чем фактически
наблюденное. Если вероятность весьма
мала, гипотезу следует отвергнуть как
неправдоподобную; при сравнительно
больших значениях вероятности ее можно
считать совместимой и опытными данными.
и по табличным значениям находится
вероятность того, что, если случайная
величина действительно распределена
по закону
,
за счет чисто случайных причин максимальное
расхождение между
и
будет не меньше, чем фактически
наблюденное. Если вероятность весьма
мала, гипотезу следует отвергнуть как
неправдоподобную; при сравнительно
больших значениях вероятности ее можно
считать совместимой и опытными данными.
Критерий Колмогорова своей простотой выгодно отличается от других критериев, в частности от критерия χ2, поэтому его весьма охотно применяют на практике. Однако, этот критерий можно применять только в случае, когда гипотетическое распределение известно заранее из каких-либо теоретических соображений, то есть когда известен не только вид функции, но и все входящие в нее параметры. Такой случай сравнительно редко встречается на практике. Если же применять этот критерий в тех случаях, когда параметры теоретического распределения выбираются по статистическим данным, критерий дает заведомо завышенные значения вероятности Р(λ), поэтому возникает риск принять как правдоподобную гипотезу, в действительности плохо согласующуюся с опытными данными.
Более информативной,
чем традиционная проверка с помощью
критического значения, является проверка
с помощью Р-значения. Р-значением
называется такое число
![]() ,
что
,
что
![]() для любого уровня значимости
,
при котором гипотеза принимается, и
для любого уровня значимости
,
при котором гипотеза принимается, и
![]() ,
для любого уровня значимости
,
при котором гипотеза отвергается. При
верной основной гипотезе Р-значение
равномерно распределено на отрезке
[0;1]. Если
,
для любого уровня значимости
,
при котором гипотеза отвергается. При
верной основной гипотезе Р-значение
равномерно распределено на отрезке
[0;1]. Если
![]() не верна, наблюдаемые Р-значения (при
достаточно высокой мощности критерия)
концентрируются около нуля. Если
Р-значение уже найдено, то решение о
принятии или отклонении гипотезы для
заданного
осуществляется на основе следующего
правила: если
не верна, наблюдаемые Р-значения (при
достаточно высокой мощности критерия)
концентрируются около нуля. Если
Р-значение уже найдено, то решение о
принятии или отклонении гипотезы для
заданного
осуществляется на основе следующего
правила: если
![]() ,
то нулевая гипотеза отвергается, если
,
то нулевая гипотеза отвергается, если![]() ,
то принимается.
,
то принимается.
Сформулируйте критерий по проверке с заданным уровнем значимости α гипотезы о равенстве нескольких генеральных средних методом дисперсионного анализа. Каким образом находится значение статистики данного критерия?
Пусть
![]() -выборка
объема ni
из нормального распределения с параметрами
мю и сигма, где i=1,…,k.
Предположим, что n=n1+…+nk
случайных величин
-выборка
объема ni
из нормального распределения с параметрами
мю и сигма, где i=1,…,k.
Предположим, что n=n1+…+nk
случайных величин
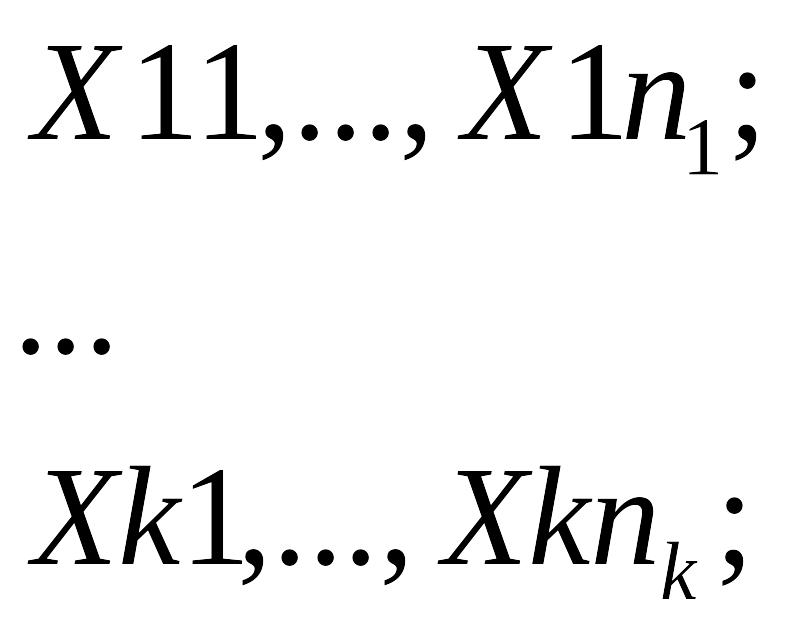
Независимы в
совокупности. Таким образом, выборки
![]() независимы и получены из нормальных
распределений с одинаковой дисперсией
сигма квадрат и, возможно, различными
средними мю1,…,мюк. Гипотеза о равенстве
всех средних одновременно записывается
как Н0: мю1=…=мюк
независимы и получены из нормальных
распределений с одинаковой дисперсией
сигма квадрат и, возможно, различными
средними мю1,…,мюк. Гипотеза о равенстве
всех средних одновременно записывается
как Н0: мю1=…=мюк
А альтернативная гипотеза – как
Н1: (![]()
Заметим, что при верной Н0 выборки являются предположениях может рассматриваться как параметрический аналог рассмотренных ранее непараметрический гипотез однородности.
Рассмотрим объединенную выборку объема n=n1+…+nk:
![]()
Интерпретируя выборки как группы, на которые разбита совокупность , введем обозначения:
![]() -выборочное
среднее в i-ой
совокупности
-выборочное
среднее в i-ой
совокупности
![]() -выборочная
дисперсия в той же выборке
-выборочная
дисперсия в той же выборке
![]() -выборочное
среднее в объединенной выборке
-выборочное
среднее в объединенной выборке
![]() -средняя
групповая дисперсия
-средняя
групповая дисперсия
![]() -межгрупповая
дисперсия
-межгрупповая
дисперсия
![]() -выборочная
дисперсия признака в объединенной
выборке
-выборочная
дисперсия признака в объединенной
выборке
![]() ,
где первое слагаемое характеризует
среднюю изменчивость признака в каждой
выборке, а второе характеризует разброс
выборочных средних.
,
где первое слагаемое характеризует
среднюю изменчивость признака в каждой
выборке, а второе характеризует разброс
выборочных средних.
Критерий Н0 против Н1 основан на следующей теореме, которую приводим без доказательства
Теорема: Пусть верна гипотеза H0, тогда
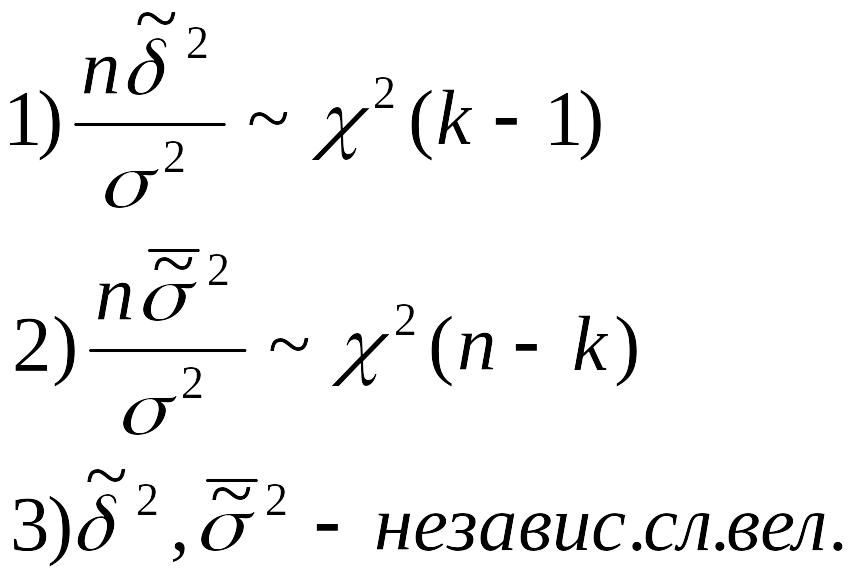
Определим F-отношение
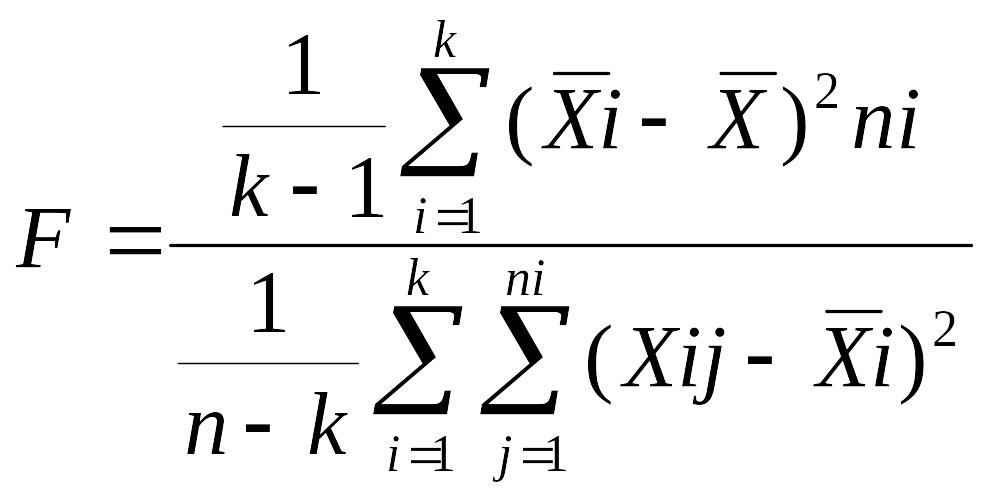
Статистику можно
представить также в виде:
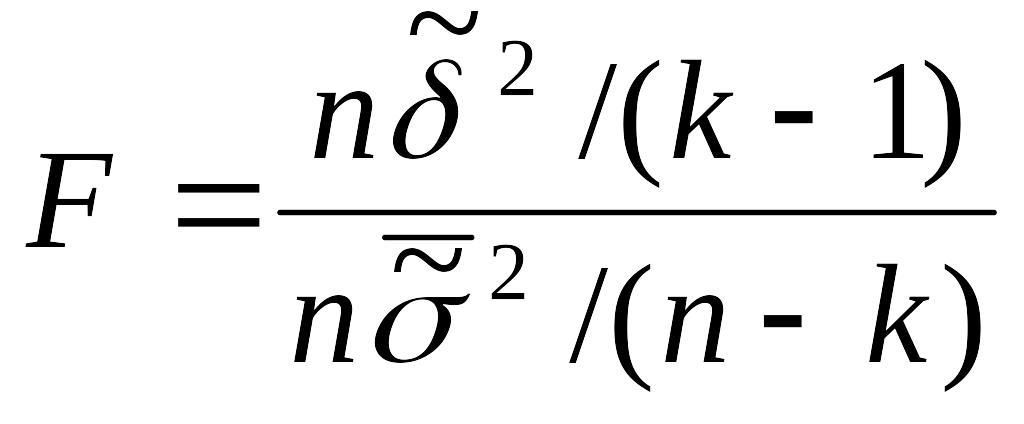
Вывод: для проверки
H0 при уровне значимости α можно
использовать критерий с критической
областью:
![]()
