1. Запишите общую формулу разложения в ряд по центральным эмпирическим моментам среднего арифметического функции от признака. Рассмотрите функцию f(x) = 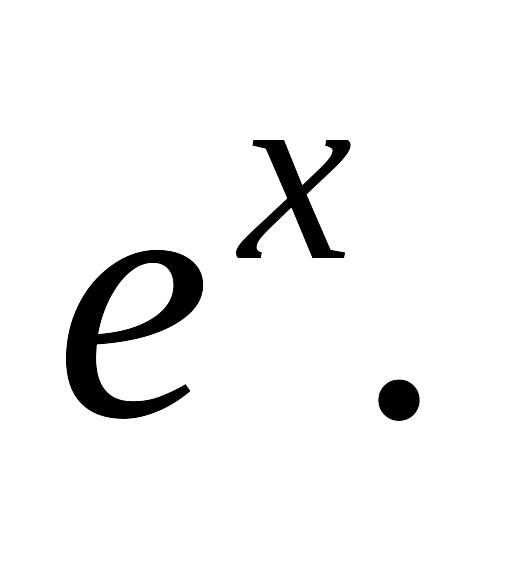По какой формуле находится приближенно среднее значение функции 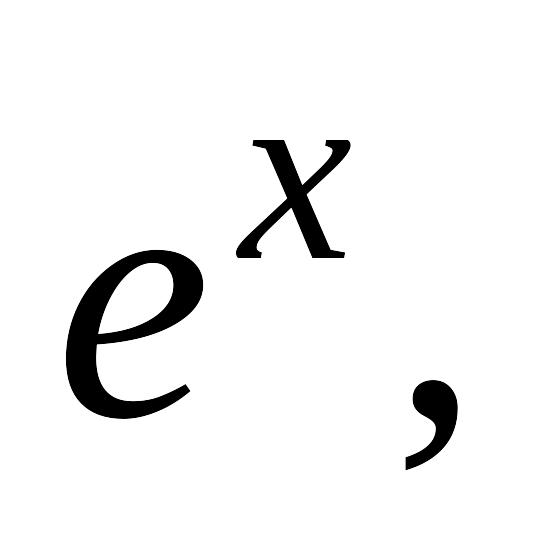если известно среднее и дисперсия σ²?

f(x) – ф-ция, ряд Тейлора кот сходится в каждой точке. . .Для f(x)= = ; .

2. Какие статистические данные называются группированными? Каким образом по интервальному распределению частот вычисляются эмпирическое среднее и эмпирическая дисперсия? В чем состоит поправка Шеппарда?

Статистические данные, представленные в виде таблиц интервальных частот, наз-ся группированными.

Эмпирич интервальн среднее: , где - середина интервала (a_i;b_i).

Эмпирич интервальн дисп-я:

Зачастую все интервалы имеют одинак длину: h=b₁-a₁=b₂-a₂=…Тогда применяют формулу: , где -поправка Шеппарда.

Поправка чаще всего применяется в тех случаях, когда эмпирическая функция распределения хорошо приближается функцией распределения нормального закона.

3. Запишите формулы для математического ожидания и дисперсии выборочной доли в случае повторной (бесповторной) выборки. Поясните все используемые обозначения.

-генеральное статистическое распределение Х

-выборочное статистическое распределение Х

Опр.: Отношение называют генеральным (выборочным) значением признака Х

Теорема: Пусть р – генеральная ( - выборочная) доля значения признака Х, . Тогда:

1)

2)

3) .

Док-во: Пусть р и - доли значения . Введем признак У:

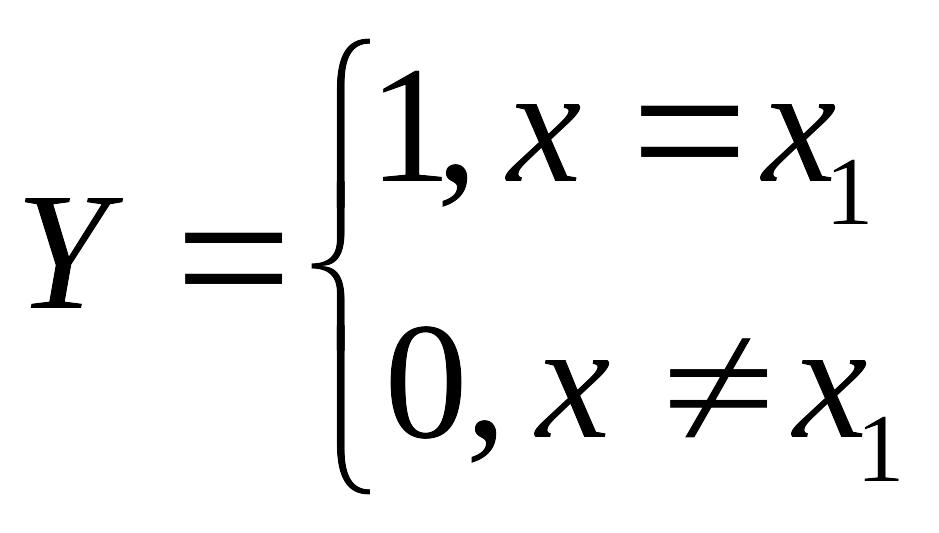
Y	0	1	Y	0	1
p	q	p	p

Выборочное распределение У

1)

2)

3)

4. Сформулируйте определение выборки из распределения. Как в этом случае определяются: выборочное среднее, выборочные начальные и центральные моменты, выборочная функция распределения?

Выборкой или выборочной совокупностью называется совокупность случайно отобранных объектов

Выборочными характеристиками признака X называют эмпирические характеристики признака X в выборочной совокупности.

Выборочное среднее- это среднее арифметическое значение признака выборочной совокупности

Если все значения x_1, x_2, …, x_n признака выборки n различны, то выборочная средняя равна:

Если же значения признака x_1, x_2, …, x_k имеют соответственно частоты n₁, n₂, …, n_k, причём n₁ + n₂ + … + n_k = n, то

Или

Начальным выборочным моментом порядка k называется среднее арифметическое k-x степеней наблюдаемых значений случайной величины

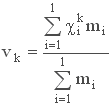где

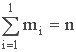
Из определения следует, что начальный выборочный момент нулевого порядка:

а начальный выборочный момент первого порядка:

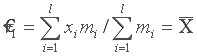
Центральным выборочным моментом порядка k называется среднее арифметическое k-x степеней отклонений наблюдаемых значений случайной величины от их среднего арифметического.

= .

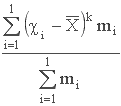Из определения следует, что центральный выборочный момент нулевого порядка:

,

центральный выборочный момент первого порядка:

Выборочная функция распределения

Это функция F*(x), определяющая для каждого значения x относительную частоту события X < x.

По определению: , где n_x – число вариант, меньших x, n – объём выборки

5. Докажите формулы для математического ожидания и дисперсии выборочного среднего в случае повторной выборки.

X₁…X_s – распределение X в основной совокупности

N₁…N_s:

Xi	X1	…	Xs
P		…

M(X_i) =

D(X_i)=D(X)

X₁…X_s – независимы для любых X_i ~ X_j

6. Выведите формулу для дисперсии выборочного среднего бесповторной выборки.

Будем считать, что - значения признака в бесповторной выборке. Так как зависимы, то нельзя утверждать, что . Заметим, что данная ковариация одинакова для всех пар , для которых . Это следует из того, что бесповторную выборку можно представить как результат одновременного извлечения всех выборочных элементов и, следовательно, совместное распределение сл. величин совпадает с совместным распределением . Предположим, что объемы выборочной и генеральной совокупностей равны. Тогда выборочное среднее является неслучайной величиной, так как .

Следовательно,

.

Отсюда найдем ковариацию : .

Для любого :

, ч.т.д.