18. Пояснив используемые символы, запишите (1–α)-доверительный (симметричный по вероятности) интервал предсказания. Для каких генеральных распределений применима данная формула?

_{Х1,…,Xn+1 – выборка из нормального распределения} в генеральной совокупности

Будем считать, что Xi-результат наблюдения Х в испытании, проводимом в момент времени i=1,…,n+1. Тогда имеет смысл следующая задача: построить по данным X1,..,Xn интервал предсказания (L,H), накрывающий Xn+1с доверительной вероятностью гамма.

Используя стандартные статистики

Построим статистику:

T= s – исправленная дисперсия

Статистика распределена по закону Стьюдента, является центральной статистикой. Построим двусторонний интервал предсказания для Xn+1, т.е. такой интервал (L,H), что L=l(X1,…,Xn), H=h(X1,…,Xn) и

Выбираем

Имеем:

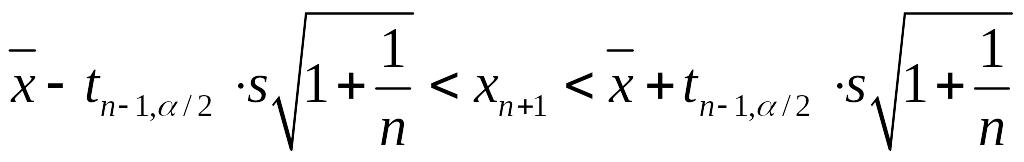
19. Запишите (1–α)-доверительную оценку сверху для математического ожидания нормального распределения с известной (неизвестной) дисперсией по выборке объема n. Почему данная оценка (неравенство) выполняется с вероятностью (1–α)?

Пусть σ² известна

1)Выберем положительные и

2)

Получаем:

и

Получаем:

-ген среднее, -ген дисперсия, АЛЬФА, n

(1-α)-доверительная оценка µ симметричная по вероятности имеет след. вид:

Теорема: Если Х1,…,Хn независимы и распределены по нормальному закону, то отношение T распределено по закону Стьюдента с n-1 степенями свободы.

Построение интервала аналогично выше приведенному, но кроме вместо процентных точек стандартного нормального распределения используются процентные точки распределения Стьюдента.

.

Опр.: Двухсторонняя интервальная оценка называется симметричной по вероятности, если

- (1 – α)-доверительная оценка сверху при изв-й дисперсии;

- (1 – α)-доверительная оценка сверху при неизв-й дисперсии;

В данном случае , то есть данная оценка сверху выполняется с вероятностью (1- ).

20. Запишите (1–α)-доверительную оценку сверху для дисперсии нормального распределения с известным (неизвестным) математическим ожиданием a по выборке объема n. Почему данная оценка (неравенство) выполняется с вероятностью (1–α)?

При известном мат. Ожидании существует эффективная точечная оценка дисперсии:

Центральная статистика:

- распределена по закону N(0,1), распределением статистики является хи квадрат.

Зависимость T0 от сигма квадрат является убывающей.

Теорема: Если и независимо, то .

Распределено по закону хи квадрат с n-1 степенями свободы.

- (1–α)-доверительная оценка сверху для дисп при известном мат ожидании

- (1–α)-доверительная оценка сверху для дисп при неизвестном мат ожидании;

В данном случае , то есть данная оценка сверху выполняется с вероятностью (1- ).

21. Опишите общую схему проверки статистических гипотез. Определите понятия: критическая область, уровень значимости, мощность критерия. Какие гипотезы называются простыми (сложными)?

Стат. гипотеза – любое утверждение о виде параметра генерального распределения. Стат. гипотеза называется параметрической, если она основана на предположении, что генеральное распределение известно с точностью до конечного числа параметров.

Параметрическая гипотеза называется простой, если она имеет вид , где - параметр распределения (возможно вектор), а - некоторое фиксированное значение параметра. Гипотеза вида , где - множество, содержащее по меньшей мере 2 элемента, называется сложной.

Пусть Н0 и Н1 – взаимоисключающие статистические гипотезы. Гипотезу Н0 назовем основной, а гипотезу Н1 – альтернативной.

Стат. Критерием с критической областью К называется правило, в соответствии с которым гипотеза , если выборка (x1,..,xn)принадлежит К и принимается, если (x1,..,xn) не принадлежит К. Как правило, критическая область задается при помощи неравенства:

с,с1,с2-критические значения, а функция t - статистика критерия.

Ошибка первого рода : отвергается верная гипотеза Но.

Ошибка второго рода: отвергается верная гипотеза Н1.

Опр: Вероятность ошибки первого рода называется уровнем значимости критерия и обозначается альфа. Вероятность ошибки второго рода обозначается бета, а величина 1-бетта называется мощностью критерия.