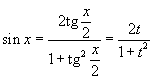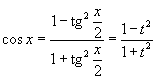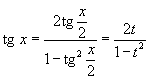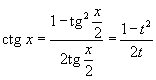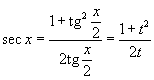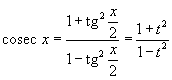- •Функции. Определение, способы задания, элементарные функции, область определения и множество значений, свойства функций. Последовательность.
- •1. Функции. Определение, способы задания, элементарные функции, область определения и множество значений, свойства функций. Последовательность.
- •Предел последовательности и функции, определение и свойства предела; неопределённости, замечательные пределы.
- •3.Непрерывность и дифференцируемость. Определение и теоремы о непрерывности.
- •4.Определение, свойства, приложения производной и дифференциала.
- •5. Основные теоремы о дифференцируемых функциях: теоремы Ферма, Ролля, Лагранжа, Коши, правило Лопиталя.
- •6. Исследование функции с помощью производной: интервалы монотонности, экстремумы функции, интервалы выпуклости, точки перегиба графика функции.
- •7. Исследование функции с помощью производной: уравнения асимптот графика функции.
- •8. Понятие о функции двух переменных. Область определения. Частные производные, полный дифференциал.
- •9. Функции n переменных. Область определения. Линии уровня. Кривые безразличия. Поверхности уровня. Предел. Непрерывность.
- •10. Функции n переменных. Градиент. Производная по направлению. Дифференцируемость и полный дифференциал.
- •11. Функции n переменных. Экстремумы. Определение. Необходимые и достаточные условия экстремума.
- •12. Неопределенный интеграл: определение, свойства, табличные интегралы.
- •13. Метод подстановки и метод интегрирования по частям.
- •14. Интегрирование рациональных алгебраических и тригонометрических выражений.
- •15. Определенный интеграл: определение, свойства, формула Ньютона-Лейбница.
- •16. Замена переменной и формула интегрирования по частям в определенном интеграле.
- •17. Геометрические приложения определенного интеграла.
- •18. Несобственные интегралы первого и второго рода. Признак сходимости несобственных интегралов.
13. Метод подстановки и метод интегрирования по частям.
Метод
подстановки.
Интегрирование путем введения новой
переменной (метод подстановки) основано
на формуле
![]() где
х = ῳ(t) - дифференцируемая функция
переменной t.
где
х = ῳ(t) - дифференцируемая функция
переменной t.
Метод
интегрирования по частям
позволяет свести исходный неопределенный
интеграл к более простому виду либо к
табличному интегралу. Этот метод наиболее
часто применяется, если подынтегральная
функция содержит логарифмические,
показательные, обратные тригонометрические,
тригонометрические функции, а также их
комбинации.Формула интегрирования по
частям следующая
![]() .То есть, подынтегральное выражение
f(x)dx представляем в виде произведения
функции u(x) на d(v(x)) - дифференциал функции
v(x). Далее находим функцию v(x) (чаще всего
методом непосредственного интегрирования)
и d(u(x)) - дифференциал функции u(x).
Подставляем найденные выражения в
формулу интегрирования по частям и
исходный неопределенный интеграл
сводится к разности
.То есть, подынтегральное выражение
f(x)dx представляем в виде произведения
функции u(x) на d(v(x)) - дифференциал функции
v(x). Далее находим функцию v(x) (чаще всего
методом непосредственного интегрирования)
и d(u(x)) - дифференциал функции u(x).
Подставляем найденные выражения в
формулу интегрирования по частям и
исходный неопределенный интеграл
сводится к разности
![]() .
Последний неопределенный интеграл
может быть взят с использованием любого
метода интегрирования, в том числе и
метода интегрирования по частям.
.
Последний неопределенный интеграл
может быть взят с использованием любого
метода интегрирования, в том числе и
метода интегрирования по частям.
14. Интегрирование рациональных алгебраических и тригонометрических выражений.
Интегрирование любого рационального выражения тригонометрических функций можно всегда свести к интегрированию алгебраической рациональной функции используя универсальную тригонометрическую подстановку x = 2arctg t (или ). Для преобразования рациональных выражений от sin x, cos x, tg x, ctg x, sec x и cosec x в алгебраические рациональные функции переменной t применяются следующие тригонометрические формулы:
|
|
|
|
|
|
Чтобы
вычислить интеграл вида
![]() , где R - рациональная функция, используется
подстановка
, где R - рациональная функция, используется
подстановка
![]() . Аналогично, для вычисления интеграла
вида
. Аналогично, для вычисления интеграла
вида
![]() , где R - рациональная функция, используется
подстановка
, где R - рациональная функция, используется
подстановка
![]() .
Если подынтегральное выражение является
только функцией tg x, то подстановка t =
tg x преобразует такой интеграл в интеграл
от рациональной функции. Для вычисления
интеграла вида
, где обе функции sin x и cos x входят в четной
степени, применяется подстановка t = tg
x и формулы
.
Если подынтегральное выражение является
только функцией tg x, то подстановка t =
tg x преобразует такой интеграл в интеграл
от рациональной функции. Для вычисления
интеграла вида
, где обе функции sin x и cos x входят в четной
степени, применяется подстановка t = tg
x и формулы
![]()
15. Определенный интеграл: определение, свойства, формула Ньютона-Лейбница.
Определение.
Определённым интегралом от функции
![]() на отрезке
на отрезке![]() называется предел интегральных сумм
при стремлении ранга разбиения к нулю
называется предел интегральных сумм
при стремлении ранга разбиения к нулю![]() , если он существует независимо от
разбиения R
и выбора точек
, если он существует независимо от
разбиения R
и выбора точек
![]() ,
т.е.
,
т.е.
![]()
Свойства. Ниже предполагается, что f (x) и g (x) - непрерывные функции на замкнутом интервале [a, b]:
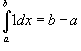 2)
2)
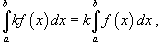 где k – константа; 3)
где k – константа; 3)
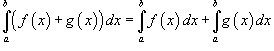 4)
4)
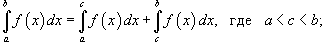 5) Если
5) Если
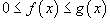 для
всех
для
всех
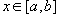 ,
то
,
то
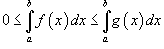 ;
6)
;
6)
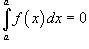 ;
7)
;
7)
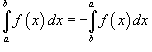 ;
8)
Если
;
8)
Если
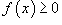 в интервале [a, b], то
в интервале [a, b], то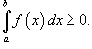 .
.
Формула
Ньютона-Лейбница. Пусть
функция f (x) непрерывна на замкнутом
интервале [a, b]. Если F (x) - первообразная
функции f (x) на [a, b], то![]()
16. Замена переменной и формула интегрирования по частям в определенном интеграле.
Замена
переменной. Определенный
интеграл
![]() по переменной x можно преобразовать в
определенный интеграл относительно
переменной t с помощью подстановки x = g
(t):
по переменной x можно преобразовать в
определенный интеграл относительно
переменной t с помощью подстановки x = g
(t):
![]() .
Новые пределы интегрирования по
переменной t определяются выражениями
.
Новые пределы интегрирования по
переменной t определяются выражениями![]() где
g -1 - обратная функция к g, т.е. t = g -1(x).
где
g -1 - обратная функция к g, т.е. t = g -1(x).
Интегрирование
по частям.
В этом случае формула интегрирования
по частям имеет вид:
![]() ,
где
,
где
![]() означает разность значений произведения
функций uv при x = b и x = a.
означает разность значений произведения
функций uv при x = b и x = a.