3.Непрерывность и дифференцируемость. Определение и теоремы о непрерывности.

Определение. Функция f(x) называется непрерывной в точке х = , если предел функции и ее значение в этой точке равны, т.е. 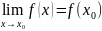. Функция y=f(x) называется дифференцируемой в точке x0, если ее приращение Δy в точке x0 может быть представлено в виде: Δy=A·Δx+α(Δx)·Δx, где A -- некоторое число, независящее от Δx, а α(Δx)-- бесконечно малая функция от переменной Δx, т.е. limΔx→0α(Δx)=0.

Теоремы непрерывности. Теорема 1. Пусть функция f (x) непрерывна в точке x = a, и C является константой. Тогда функция Сf (x) также непрерывна при x = a.

Теорема 2. Даны две функции f (x) и g (x), непрерывные в точке x = a. Тогда сумма этих функций f (x) + g (x) также непрерывна в точке x = a.

Теорема 3. Предположим, что две функции f (x) и g (x) непрерывны в точке x = a. Тогда произведение этих функций f (x) g (x) также непрерывно в точке x = a.

Теорема 4. Даны две функции f (x) и g (x), непрерывные при x = a. Тогда отношение этих функций также непрерывно при x = a при условии, что

Теорема 5. Предположим, что функция f (x) является дифференцируемой в точке x = a. Тогда функция f (x) непрерывна в этой точке (т.е. из дифференцируемости следует непрерывность функции в точке; обратное − неверно).

Теорема 6 (Теорема о предельном значении).

Если функция f (x) непрерывна на закрытом и ограниченном интервале [a, b], то она ограничена сверху и снизу на данном интервале. Другими словами, существуют числа m и M, такие, что для всех x в интервале [a, b] ( рис. 1).

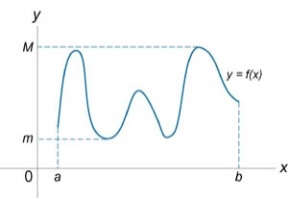
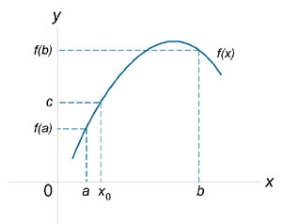
Рис.1 Рис.2

Теорема 7 (Теорема о промежуточном значении). Пусть функция f (x) непрерывна на закрытом и ограниченном интервале [a, b]. Тогда, если c − некоторое число, большее f (a) и меньшее f (b), то существует число x0, такое, что

(рис.2).

4.Определение, свойства, приложения производной и дифференциала.

Определение. 1)Пусть в некоторой окрестности точки определена функция Производной функции называется такое число А, что функцию в окрестности можно представить в виде если А существует. 2) Дифференциалом функции называется линейная часть приращения функции относительно приращения аргумента

Δ f = A·Δx + o(Δx),т.е. df = A·Δx.

Свойства.1) Производных:

2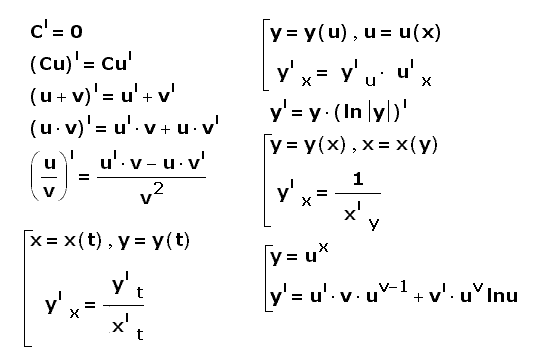 )Дифференциала: 1) Дифференциал постоянной равен нулю: dc = 0, с = const 2)Дифференциал суммы дифференцируемых функций равен сумме дифференциалов слагаемых:

d(u+v)=du + dv 3) Следствие. Если две дифференцируемые функции отличаются постоянным слагаемым, то их дифференциалы равны d(u+c) = du (c= const). 4)Дифференциал произведения двух дифференцируемых функций равен произведению первой функции на дифференциал второй плюс произведение второй на дифференциал первой: d(uv) = udv + vdu. 5) Следствие. Постоянный множитель можно выносить за знак дифференциала d(cu) = cdu (с = const).6)Дифференциал частного u/v двух дифференцируемых функций и = и(х) и v = v(x) определяется формулой . 7) Свойство независимости вида дифференциала от выбора независимой переменной (инвариантность формы дифференциала): дифференциал функции равен произведению производной на дифференциал аргумента независимого от того, является ли этот аргумент независимой переменной или функцией другой независимой переменной.