
- •Функции. Определение, способы задания, элементарные функции, область определения и множество значений, свойства функций. Последовательность.
- •1. Функции. Определение, способы задания, элементарные функции, область определения и множество значений, свойства функций. Последовательность.
- •Предел последовательности и функции, определение и свойства предела; неопределённости, замечательные пределы.
- •3.Непрерывность и дифференцируемость. Определение и теоремы о непрерывности.
- •4.Определение, свойства, приложения производной и дифференциала.
- •5. Основные теоремы о дифференцируемых функциях: теоремы Ферма, Ролля, Лагранжа, Коши, правило Лопиталя.
- •6. Исследование функции с помощью производной: интервалы монотонности, экстремумы функции, интервалы выпуклости, точки перегиба графика функции.
- •7. Исследование функции с помощью производной: уравнения асимптот графика функции.
- •8. Понятие о функции двух переменных. Область определения. Частные производные, полный дифференциал.
- •9. Функции n переменных. Область определения. Линии уровня. Кривые безразличия. Поверхности уровня. Предел. Непрерывность.
- •10. Функции n переменных. Градиент. Производная по направлению. Дифференцируемость и полный дифференциал.
- •11. Функции n переменных. Экстремумы. Определение. Необходимые и достаточные условия экстремума.
- •12. Неопределенный интеграл: определение, свойства, табличные интегралы.
- •13. Метод подстановки и метод интегрирования по частям.
- •14. Интегрирование рациональных алгебраических и тригонометрических выражений.
- •15. Определенный интеграл: определение, свойства, формула Ньютона-Лейбница.
- •16. Замена переменной и формула интегрирования по частям в определенном интеграле.
- •17. Геометрические приложения определенного интеграла.
- •18. Несобственные интегралы первого и второго рода. Признак сходимости несобственных интегралов.
8. Понятие о функции двух переменных. Область определения. Частные производные, полный дифференциал.
Понятие
о функции двух переменных. Если
указано правило, согласно которому с
каждой точкой М плоскости сопоставляется
некоторое число u, то говорят, что на
плоскости «задана функция точки»;
задание функции символически выражается
равенством вида u=f(M). Число u, сопоставляемое
с точкой М, называется значением данной
функции в точке М. Функция двух переменных
x и y обозначается символом f(x; y): если
f(M)=f(x;y), то формула u=f(x; y) называется
выражением данной функции в выбранной
системе координат. Так, в предыдущем
примере f(M)=AM; если ввести декартову
прямоугольную систему координат с
началом в точке А, то получим выражение
этой функции:
![]() .
.
Область
определения функции.
Например функция z = f ( x, y ) двух переменных
изобразится в виде некоторого множества
точек на плоскости Oxy. Так, например,
областью определения функции
![]() является
множество точек плоскости Oxy, координаты
которых удовлетворяют соотношению
является
множество точек плоскости Oxy, координаты
которых удовлетворяют соотношению
![]() т.
е. представляет собой круг радиуса r с
центром в начале координат.
т.
е. представляет собой круг радиуса r с
центром в начале координат.
Частные
производные, полный дифференциал.
Частной
производной по х от функции
![]() называется
предел отношения частного приращения
этой функции
называется
предел отношения частного приращения
этой функции
![]() по х к приращению
по х к приращению
![]() ,
когда последнее стремится к нулю:
,
когда последнее стремится к нулю:
![]() . Частной производной по у от функции
называется предел отношения частного
приращения этой функции по у к приращению
. Частной производной по у от функции
называется предел отношения частного
приращения этой функции по у к приращению
![]() , когда последнее стремится к нулю:
, когда последнее стремится к нулю:
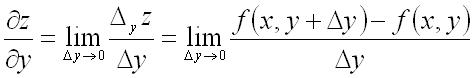 . Пусть задана функция
. Если аргументу х сообщить приращение
, а аргументу у – приращение
, то функция
получит приращение
. Пусть задана функция
. Если аргументу х сообщить приращение
, а аргументу у – приращение
, то функция
получит приращение
![]() , которое называется полным приращением
функции и определяется формулой:
, которое называется полным приращением
функции и определяется формулой:
![]() . Функция
,
полное приращение
которой в данной точке может быть
представлено в виде суммы двух слагаемых
:
. Функция
,
полное приращение
которой в данной точке может быть
представлено в виде суммы двух слагаемых
:
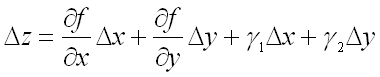 ,где
,где
![]() и
и
![]() стремятся к нулю, когда
и
стремятся к нулю, называется дифференцируемой
в данной точке. Линейная часть полного
приращения функции называется полным
дифференциалом и обозначается
стремятся к нулю, когда
и
стремятся к нулю, называется дифференцируемой
в данной точке. Линейная часть полного
приращения функции называется полным
дифференциалом и обозначается
![]() :
:
![]() ,
где
,
где
![]() и
и
![]() – дифференциалы независимых переменных,
которые, по определению, равны
соответствующим приращениям
и
.
Частные производные от частных производных
первого порядка называются частными
производными второго порядка. Для
функции двух переменных
их четыре:
– дифференциалы независимых переменных,
которые, по определению, равны
соответствующим приращениям
и
.
Частные производные от частных производных
первого порядка называются частными
производными второго порядка. Для
функции двух переменных
их четыре:
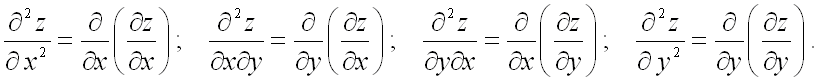
9. Функции n переменных. Область определения. Линии уровня. Кривые безразличия. Поверхности уровня. Предел. Непрерывность.
Переменная z называется функцией двух независимых переменных х,у в множестве М, если каждой паре (х,у) из множества М по некоторому правилу или закону ставится в соответствие одно определенное значение z из Z.
Множество М, в котором заданы переменные х,у, называется областью определения функции, а сами х,у — ее аргументами.Обозначения: z = f(x,y), z = z(x,y). Замечание. Так как пару чисел (х,у) можно считать координатами некоторой точки на плоскости, будем впоследствии использовать термин «точка» для пары аргументов функции двух переменных, а также для упорядоченного набора чисел , являющихся аргументами функции нескольких переменных.
Переменная z (с областью изменения Z) называется функцией нескольких независимых переменных в множестве М, если каждому набору чисел из множества М по некоторому правилу или закону ставится в соответствие одно определенное значение z из Z. Понятия аргументов и области определения вводятся так же, как для функции двух переменных.Обозначения: z = f, z = z.
Линии и поверхности уровня.Для функции двух переменных, заданной уравнением (1.1), можно рассмотреть множество точек (х,у) плоскости Оху, для которых z принимает одно и то же постоянное значение, то есть z = const. Эти точки образуют на плоскости линию, называемую линией уровня.
Предел и непрерывность функции нескольких переменных. Введем понятие δ-окрестности точки М0 (х0 , у0) на плоскости Оху как круга радиуса δ с центром в данной точке. Аналогично можно определить δ-окрестность в трехмерном пространстве как шар радиуса δ с центром в точке М0 (х0 , у0 , z0). Для n-мерного пространства будем называть δ-окрестностью точки М0 множество точек М с координатами , удовлетворяющими условию где - координаты точки М0. Иногда это множество называют «шаром» в n-мерном пространстве.
Число А называется пределом функции нескольких переменных fв точке М0, если такое, что | f(M) — A| < ε для любой точки М из δ-окрестности М0.Необходимо учитывать, что при этом точка М может приближаться к М0, условно говоря, по любой траектории внутри δ-окрестности точки М0. Поэтому следует отличать предел функции нескольких переменных в общем смысле от так называемых повторных пределов, получаемых последовательными предельными переходами по каждому аргументу в отдельности.
Функция f называется непрерывной в точке М0, если (1.2)Если ввести обозначения , то условие (1.2) можно переписать в форме (1.3).
