2.Уравнение плоской гармонической волны и её основный параметры. Фазовая скорость. Волновой пакет. Групповая скорость

Уравнением волны называется выражение, которое дает смещение колеблющейся частицы как функцию ее координат x, y, z и времениt: ,

где имеются в виду координаты равновесного положения частицы. Найдем вид функции в случае плоской волны, предполагая, что колебания носят гармонический характер. Для простоты направим оси координат так, чтобы ось x совпадала с направлением распространения волны. Тогда волновые поверхности будут перпендикулярными к оси x и, поскольку все точки волновой поверхности колеблются одинаково, смещение будет зависеть только от x и t: Пусть колебания точек, лежащих в плоскости , имеют вид: .

Найдем вид колебания точек в плоскости, соответствующей произвольному значению x. Для того, чтобы пройти путь от плоскости до этой плоскости, волне требуется время , где v - скорость распространения волны. Следовательно, колебания частиц, лежащих в плоскости x, будут отставать по времени на  от колебаний частиц в плоскости , т.е. будут иметь вид: Итак, уравнение плоской волны, распространяющейся в направлении оси x, выглядит следующим образом:

Начальная фаза волны определяется выбором начал отсчета x и t. При рассмотрении одной волны начала отсчета времени и координаты обычно выбираются так, чтобы . Зафиксируем какое-либо значение фазы, положив

.

Это выражение определяет связь между временем t и тем местом x, в котором фаза имеет зафиксированное значение. Вытекающее из него значение dx/dt дает скорость, с которой перемещается данное значение фазы. Продифференцировав указанное выше выражение, получим

.

Таким образом, скорость распространения волны vесть скорость перемещения фазы, в связи с чем ее называют фазовой скоростью.

Уравнению плоской волны можно придать симметричный относительно x и t вид (полагаем ):

,

где введена величина 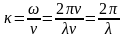, которая называется волновым числом. Таким образом

-- уравнение плоской бегущей волны, распространяющейся вдоль оси x,где - волновое число. Или .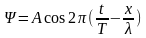

Теперь найдем уравнение сферической волны. Амплитуда колебаний в этом случае убывает с расстоянием от источника по закону 1/r. Тогда получим - уравнение сферической волны,гдеА - постоянная величина, численно равная амплитуде на расстоянии от источника, равном единице.

3.Волновое уравнение

Уравнение любой волны является решением дифференциального уравнения, называемого волновым. Чтобы установить вид волнового уравнения, сопоставим вторые частные производные по координатам и по времени от функции , описывающей плоскую волну. Для простоты рассмотрим плоскую волну, распространяющуюся вдоль оси x:

.

Продифференцировав эту функцию дважды по t и дважды по x, получим

, , , (1)

, , ,(2)

Сопоставив (1) и (2) и заменив через , получим волновое уравнение, где v- скорость волны.

В случае плоской волны, распространяющейся в произвольном направлении, аналогичным образом получим:

.

Если ввести дифференциальный оператор Лапласа: ,

волновое уравнение можно записать в виде:

-волновое уравнение.

4.Фазовая скорость волны в твёрдых телах

В однородных твёрдых телах могут существовать два типа объемных волн, отличающихся друг от друга поляризацией колебаний относительно направления распространения волны: продольная (P-волна) и поперечная (S-волна). Скорость распространения первой (Ср) всегда выше, чем скорость второй (Сs):

где K — модуль всестороннего сжатия; G — модуль сдвига; E — модуль Юнга; ν — коэффициент Пуассона. Как и для случая с жидкой или газообразной средой, при расчетах должны использоваться адиабатические модули упругости.

В многофазных средах из-за явлений неупругого поглощения энергии скорость звука, вообще говоря, зависит от частоты колебаний (то есть наблюдается дисперсия скорости). Например, оценка скорости упругих волн в двухфазной пористой среде может быть выполнена с применением уравнений теории Био-Николаевского. При достаточно высоких частотах (выше частоты Био) в такой среде возникают не только продольные и поперечные волны, но также и продольная волна II-рода. При частоте колебаний ниже частоты Био, скорость упругих волн может быть приблизительно оценена с использованием гораздо более простых уравнений Гассмана.

При наличии границ раздела, упругая энергия может передаваться посредством поверхностных волн различных типов, скорость которых отличается от скорости продольных и поперечных волн. Энергия этих колебаний может во много раз превосходить энергию объемных волн.