38.Автономные системы на плоскости.

Рассмотрим автономную двумерную систему

(1), где вектор-функция 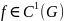, из пространства .

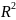Сначала изучим поведение траекторий системы (1) в линейном случае, т.е. когда она имеет вид 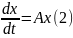, где 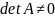при этом предположим, что система (2) имеет единственное состояние равновесия и оно расположено в точке О(0,0).

С помощью линейного невырожденного преобразования x=Sy систему (2) приведем к виду 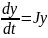(3), где 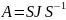J-вещественная нормальная форма жардана матрицыA.

В зависимости от вида формы жордана J рассмотрим случаи:

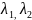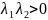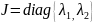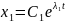
Случай 1: Собственные числа матрицы A вещественны, различны и . В этом случае жорданова форма . Параметрические ур.траектории системы(3) 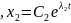Расположение траекторий при

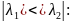
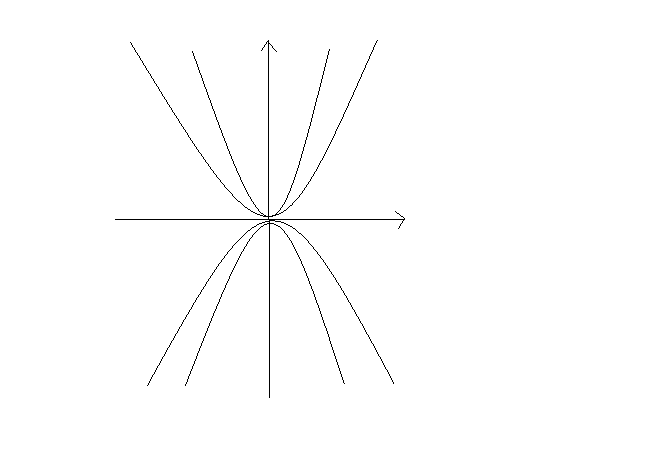-узел (бикритический узел). Состояние равновесия О-узел.

Случ.2: 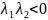и вещественны. Состояние равновесия – седло. Геометрическая картина:

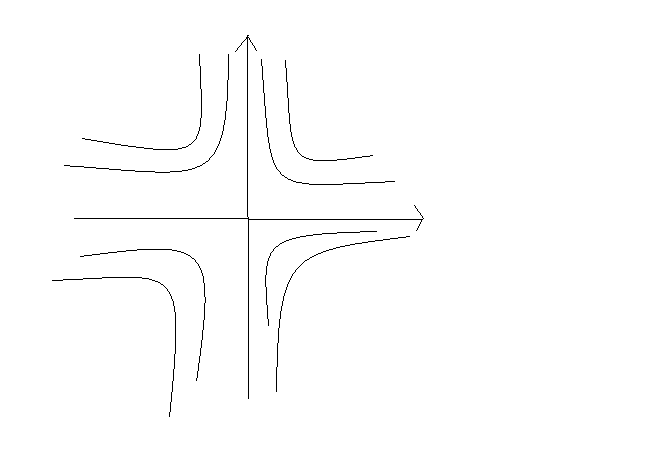
Случ.3: Корни характеристического ур.системы (2) комплексно сопряженные и при этом 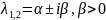. Форма жордана имеет вид 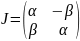. Перейдем к полярным координатам и в результате получим систему 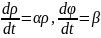. Отсюда получаем параметрические ур.траекторий в виде 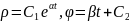. При 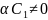траектории образуют спираль. Состояние равновесия – фокус. 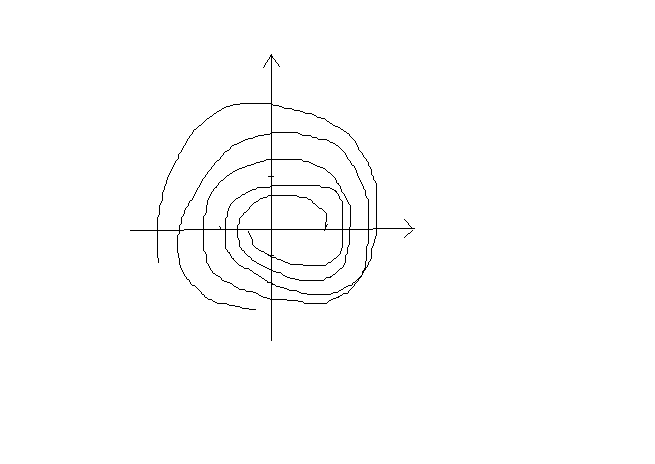Если α=0, то центр

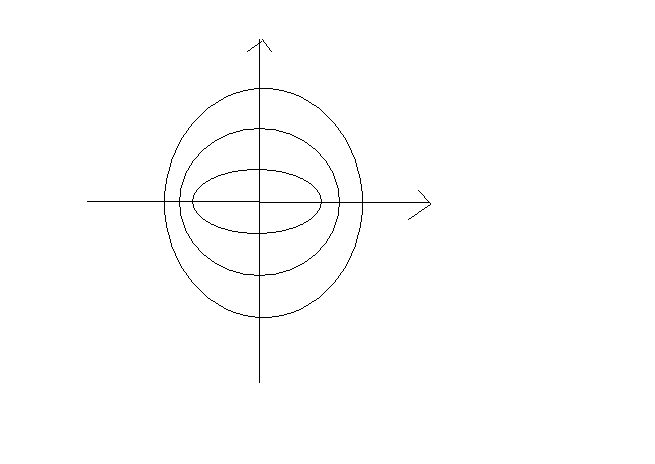
Случ.4: Собственные числа матрицы A 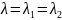, а нормальная форма жордана имеет вид .Траектории системы расположены на кривых

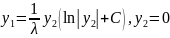
Расположение траекторий – монокритический узел:

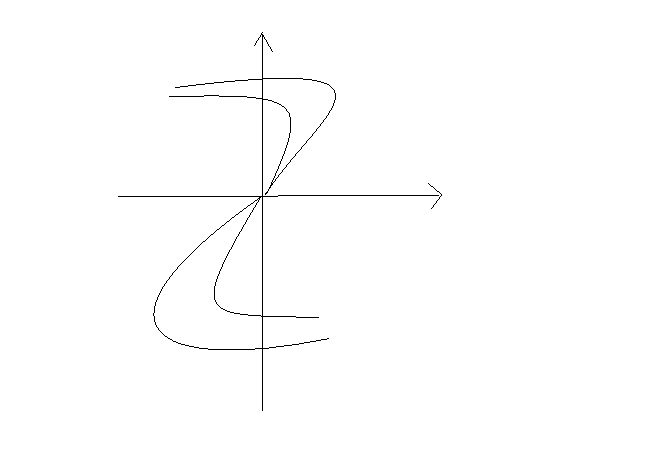
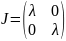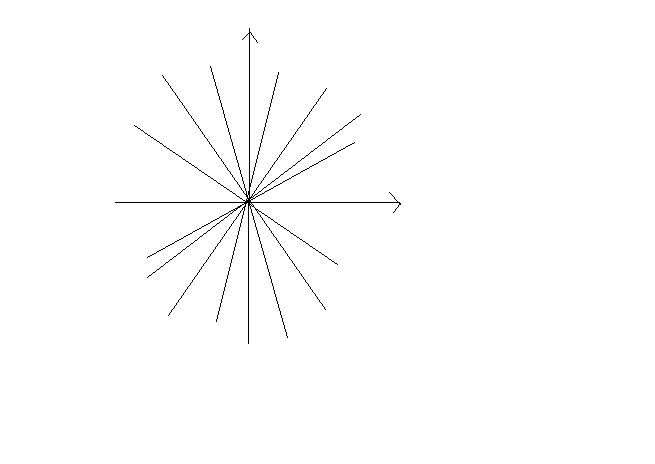
Случ.5: Собственные числа , а нормальная жорданова форма имеет вид: . Траектории системы (3) расположены на прямых 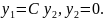Картина расположения траекторий – дикритический узел:

11. Интегрирующий множитель

Рассмотрим ур-ние 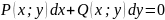(1), где 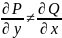на области G.

Опр.1: Непрерывно диффер. и не обращающийся в ноль на области G будем назыв. интегрирующим множителем ур-ния (1), если на обл. G ур-ние 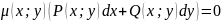явл. ур-нием полных диф-лов, если для ур-ния (1) существуетет интегр-щий множитель Q, то в силу 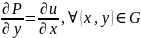он должен удолетв. соотношению:

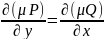
На основании его получаем диф. ур-ние частных производных для определ. ф-ции :

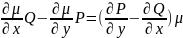(2).

Решение данного диф-ного ур-ния не проще, чем решение исходного диф-ного ур-ния (1).

Отметим, что нас интересует лишь какое-либо решение ур-ния (1).

На практике данное решение можно найти из каких-либо особенностей инт-щего множителя. Чаще всего его ищут либо , либо , тогда ур-ние (2) для нахождения ф-ции упрощают.

В некотором случае решение диф. ур-ний вида (1) можно применять метод выделения полных диф. используя известные ф-лы:

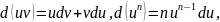
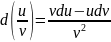
Если в диф-ном ур-нии (1) можно выделить полный диф-ал в некоторой ф-ции 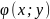, то иногда данное уравнение можно упростить выполнив замену .