
- •22. Линейные однородные уравнения в частных производных 1-го порядка.
- •23.Квазилинейное уравнение в частных производных 1-го порядка.
- •24.Уравнение Пфаффа.
- •25. Линейные дифференциальные уравнения порядка n с переменными коэффициентами
- •26. Линейные однородные д.У. Порядка n.
- •27.Линейные неоднородные уравнения порядка n.
- •28. Линейные однородные дифференциальные уравнения n порядка с постоянными коэффициентами.
- •29. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами и правой частью специального вида
- •30.Линейные однородные системы дифф.Ур.
- •31.Линейные неоднородные системы дифф. Ур.
- •32.Линейные однородные системы с постоянными коэффициентами.
- •33.Линейные неоднородные системы с постоянными коэффициентами и правой частью специального вида.
- •34. Линейные однородные системы с периодическими коэффициентами.
- •35.Устойчивость дифференциальных систем.
- •36.Метод функции Ляпунова.
- •37.Автономные системы.
- •38.Автономные системы на плоскости.
- •11. Интегрирующий множитель
25. Линейные дифференциальные уравнения порядка n с переменными коэффициентами
Опр. Линейным дифференциальным уравнением порядка n будем называть уравнение вида
 (1)
(1)
Где
функции
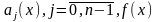 -
непрерывны на отрезке [a;b],
при этом известные функции
-
непрерывны на отрезке [a;b],
при этом известные функции
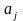 называются коэффициентами уравнения
(1),а заданная функция f(x)
– правой частью уравнения (1).
называются коэффициентами уравнения
(1),а заданная функция f(x)
– правой частью уравнения (1).
Опр.
Если в уравнении (1) функция
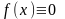 на
[a;b],то
данное уравнение называют линейным
однородным.
В противном случае уравнение (1) называют
неоднородным линейным.
на
[a;b],то
данное уравнение называют линейным
однородным.
В противном случае уравнение (1) называют
неоднородным линейным.
В
дальнейшем будем считать, что коэффициенты
уравнения (1) и его правая часть могут
принимать вообще говоря комплексные
значения
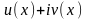
Опр. Комплекснозначную функцию y=f(x) будем называть решением уравнения (1) на [a;b],если она n-раз непрерывно дифференцируема на [a;b] и обращает данное уравнение в верное тождество.
Непосредственным образом проверяются следующее утверждение:
Лемма1
(принцип
суперпозиции для уравнения (1)
) Если
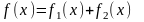 и
и
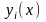 есть решение уравнения (1) при
есть решение уравнения (1) при
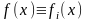 на [a;b]
,
на [a;b]
,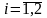 ,
то функция
,
то функция
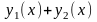 есть
решение уравнения (1) .
есть
решение уравнения (1) .
Следствие1.
Если
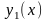 и
и
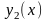 есть решения линейного однородного
уравнения,
есть решения линейного однородного
уравнения,
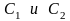 -
произвольные числа (постоянные), то их
линейная комбинация
-
произвольные числа (постоянные), то их
линейная комбинация
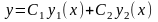 также является решением исходного
линейного однородного уравнения.
также является решением исходного
линейного однородного уравнения.
Решение
уравнения (1) всегда можно свести к
решению линейной системы дифференциальных
уравнений порядка n
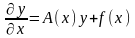 (2),
(2),
где
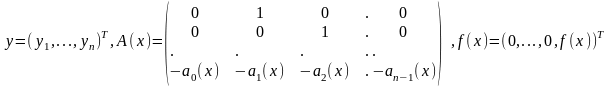
Лемма2 Уравнение (1) эквивалентно системе (2) .
Доказательство
осуществляется на основании замены
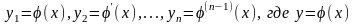 есть решение уравнения (1).
есть решение уравнения (1).
Данная лемма позволяет перенести все результаты для линейных систем на случай линейного уравнения (1)
Рассмотрим для дифференциального уравнения (1) начальные условия
(3)

 -есть
заданные числа
-есть
заданные числа
Теорема
1 Пусть
все функции
 -непрерывны
на
-непрерывны
на
 и пусть точка
и пусть точка
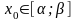 .Тогда
при произвольных начальных значениях
.Тогда
при произвольных начальных значениях
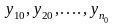 решение
задачи Коши (1) ,(3) существует и единственно
на всем отрезке
.
решение
задачи Коши (1) ,(3) существует и единственно
на всем отрезке
.
Доказательство:
выполним замену
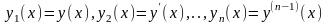 .В
результате этой замены уравнение (1)
сводится к системе (2).При этом начальные
условия (3) примут вид
.В
результате этой замены уравнение (1)
сводится к системе (2).При этом начальные
условия (3) примут вид
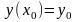 (4)
,где
(4)
,где
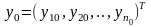 . В силу леммы 2 задача Коши (1) и (3)
эквивалентно задачи Коши (2) и (4).
. В силу леммы 2 задача Коши (1) и (3)
эквивалентно задачи Коши (2) и (4).
В силу условий теоремы 1 матрицы А(х),F(x) –непрерывны на .
Согласно соответствующей теоремы для линейной системы решение задачи Коши (2),(4) существует и единственно на .
Поэтому
и решение задачи Коши (1),(3) существует
и единственно на
.
Следствие
2 Задача
Коши
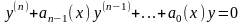 (5)
(5)
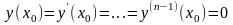 (6)
(6)
Где
функции
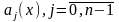 -непрерывны
на
имеет единственное решение
-непрерывны
на
имеет единственное решение
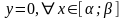 .
.
Доказательство: В самом деле тождественный нуль на есть решение задачи Коши (5),(6),а оно единственно в силу теоремы 1.
Отметим , что в отличии от нелинейного уравнения теорема 1 гарантирует существование и единственность решения задачи Коши (1),(3) глобальна(т.е. на всем ).
26. Линейные однородные д.У. Порядка n.
Рассмотрим лин. однородное д.у. порядка n
 (1),
где
(1),
где
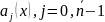 непрерывны на
непрерывны на
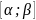 .
.
f(x)
Опр.1
Решение
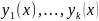 уравнения (1) будем наз. линейно зависимым
на
существуют такие числа
уравнения (1) будем наз. линейно зависимым
на
существуют такие числа
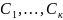 одновременно
неравные нулю и при этом имеет место
неравенство
одновременно
неравные нулю и при этом имеет место
неравенство
 ,
в противном случае решение
,
в противном случае решение
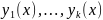 будет наз. линейно независимым на
будет наз. линейно независимым на
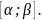
Лемма
1.
Решения
уравнения (1) линейно зависимы на
тогда и только тогда, когда соответствующее
им решение
системы
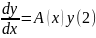 ,
эквивалентной уравнению (1) линейно
зависимы на
(
при этом вектор в столбце
,
эквивалентной уравнению (1) линейно
зависимы на
(
при этом вектор в столбце
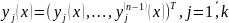 ).
).
следствие 1.решение уравн. (1) линейно независимы тогда и только тогда когда лин. нез. на этом отрезке соответствующие векторные решения системы (2).
Опр.2.
совокупность
произвольных n
линейно независимых решений
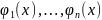 уравнения (1) на
будем наз. Фундаментальной системой
решений этого уравнения.
уравнения (1) на
будем наз. Фундаментальной системой
решений этого уравнения.
Лемма
2. Решения
образуют фундаментальную систему
решений уравнения (1) тогда и только
тогда когда вектор-функции
 компанентами
компанентами
 ,
,
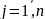 образуют фундаментальную систему
решений линейной однородной системы
(2).
образуют фундаментальную систему
решений линейной однородной системы
(2).
qсистемы переж. фундам. сис-му лин. уравнений.
Теорема 1. Для уравн. (1)существует бесконечное мн-во фундаментальных систем решений.
Теорема
2. Если
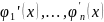 eсть
фундаментальная сис-ма решений
диф.ур.(1) , то любое решение y(x)
этого уравнения представима в виде
y(x)
=
eсть
фундаментальная сис-ма решений
диф.ур.(1) , то любое решение y(x)
этого уравнения представима в виде
y(x)
=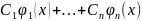 (3), где
(3), где
 есть некоторые постоянные.
есть некоторые постоянные.
Опр.
3. Функция
вида (3), где
есть фундаментальная система решений
уравн. (1), а
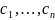 произвольные параметры наз. Общим реш.
Уравн. (1).
произвольные параметры наз. Общим реш.
Уравн. (1).
Опр.4.
Определителем
Вронского(Вранскианом)решений
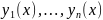 уравн. (1) будем наз. определитель n-го
порядка
уравн. (1) будем наз. определитель n-го
порядка
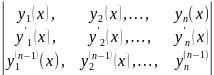 (4)
(4)
Данный
определитель будем обозначать символом
W(x)
или W
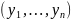 .
.
Теорема
3. Решение
уравнения (1) линейно зависимы тогда и
только тогда , когда W(x)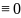 на
на
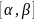 .
Решение
лин. нез. на
тогда и только тогда, когда W(x)
.
Решение
лин. нез. на
тогда и только тогда, когда W(x)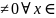 .
.
Теорема
4.
Пусть W(x)
есть определитель Вронского реш.
уравнения (1) и точка
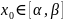 ,
тогда для всех
,
тогда для всех
 справедлива формула Лиувиля Остраградского:
справедлива формула Лиувиля Остраградского:
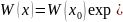 (5)
(5)
Док-во данной теоремы вытекает из формулы (5) для системы (2).
