
- •22. Линейные однородные уравнения в частных производных 1-го порядка.
- •23.Квазилинейное уравнение в частных производных 1-го порядка.
- •24.Уравнение Пфаффа.
- •25. Линейные дифференциальные уравнения порядка n с переменными коэффициентами
- •26. Линейные однородные д.У. Порядка n.
- •27.Линейные неоднородные уравнения порядка n.
- •28. Линейные однородные дифференциальные уравнения n порядка с постоянными коэффициентами.
- •29. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами и правой частью специального вида
- •30.Линейные однородные системы дифф.Ур.
- •31.Линейные неоднородные системы дифф. Ур.
- •32.Линейные однородные системы с постоянными коэффициентами.
- •33.Линейные неоднородные системы с постоянными коэффициентами и правой частью специального вида.
- •34. Линейные однородные системы с периодическими коэффициентами.
- •35.Устойчивость дифференциальных систем.
- •36.Метод функции Ляпунова.
- •37.Автономные системы.
- •38.Автономные системы на плоскости.
- •11. Интегрирующий множитель
27.Линейные неоднородные уравнения порядка n.
Рассмотрим
линейное неоднородное дифференциальное
уравнение n-го
порядка
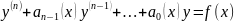 (1)
(1)
где 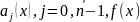 —непрерывные
на [α,β]
функции.
—непрерывные
на [α,β]
функции.
Вместе
с ур.(1) рассмотрим соответствующее ему
линейное однородное ур.
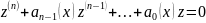 (2).
(2).
Т.1:
Пусть
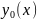 есть какое-либо решение уравнения (1) и
есть какое-либо решение уравнения (1) и
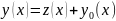 .
Тогда y(x)
является решением уравнения (1) тогда и
только тогда, когда z(x)
есть решение уравнения (2).
.
Тогда y(x)
является решением уравнения (1) тогда и
только тогда, когда z(x)
есть решение уравнения (2).
Из
Т.1 вытекает, что если известна
фундаментальная система решений
однородного
уравнения (2), то функция
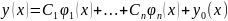 (4), где
(4), где
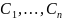 -
произвольные параметры, а
-
частное решение неоднородного уравнения
(1), является общим решением дифф.ур. (1).
-
произвольные параметры, а
-
частное решение неоднородного уравнения
(1), является общим решением дифф.ур. (1).
Покажем
, как можно в этом случае при
 найти решение неоднородного уравнения
(1) удовлетворяющее нулевым начальным
условиям
найти решение неоднородного уравнения
(1) удовлетворяющее нулевым начальным
условиям
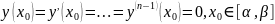 (5).
(5).
Пусть
K(x)
есть решение однородного ур. (2)
удовлетворяющее начальным условиям
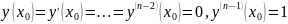 (6).
(6).
Построим
K(x).
Если
есть ФСР ур. (2), то в силу фор.(3) имеем
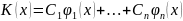 .
Подставим K(x)
в начальные условия (6). Разрешая полученную
систему находим, что
.
Подставим K(x)
в начальные условия (6). Разрешая полученную
систему находим, что
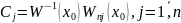 ,
где
,
где
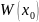 -
определитель Вронского системы функций
в точке
-
определитель Вронского системы функций
в точке
 ,
а
,
а
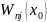 -
алгебраическое дополнение элемента
-
алгебраическое дополнение элемента
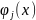 в определителе
.
Получаем
в определителе
.
Получаем
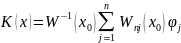 (7).
(7).
Т.2:
Функция
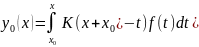 ,
где
,
где
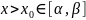 является частным решением дифф.ур. (1)
удовлетворяющим нулевым начальным
условиям (5).
является частным решением дифф.ур. (1)
удовлетворяющим нулевым начальным
условиям (5).
28. Линейные однородные дифференциальные уравнения n порядка с постоянными коэффициентами.
Рассмотрим
линейное однородное д.у. n
порядка с постоянными коэффициентами
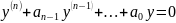 (1.25).
Здесь
(1.25).
Здесь
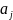 ,
ј=
,
ј=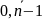 есть вещественные числа. Введем
символический оператор
есть вещественные числа. Введем
символический оператор
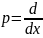 ,
который обозначает дифференцирование
по переменной x.
При этом представим производные
,
который обозначает дифференцирование
по переменной x.
При этом представим производные
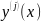 как степени оператора
как степени оператора
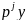 .
Будем считать, что при ј=0 степень данного
оператора равна самой фу-ии (1.25).
Левую часть можно записать в виде
+…+
.
Будем считать, что при ј=0 степень данного
оператора равна самой фу-ии (1.25).
Левую часть можно записать в виде
+…+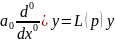 ,
где
,
где
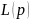 =
=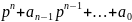 .
Очевидно, что
есть многочлен степени n
от оператора p.
Это позволяет вместо д.у.
1.25.
записывать операторное ура-ие
.
Очевидно, что
есть многочлен степени n
от оператора p.
Это позволяет вместо д.у.
1.25.
записывать операторное ура-ие
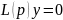 (2.25).
Будем искать частные решения д.у. 1.
25.
В виде
(2.25).
Будем искать частные решения д.у. 1.
25.
В виде
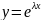 (3.25).
Подставляя фу-ию 3.25.
получаем, что
(3.25).
Подставляя фу-ию 3.25.
получаем, что
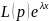 =
=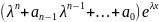 =0. Отсюда видно, что λ является корнем
алгебраического ура-ия
=0. Отсюда видно, что λ является корнем
алгебраического ура-ия
 (4.25),
то фу-ия 3.25
есть решение д.у. 1.25
(4.25),
то фу-ия 3.25
есть решение д.у. 1.25
Рассмотрим
сначала случай, когда все корни 4.25
веще-ые и различные. Им соответ. n-
решений
 ,
,
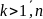
Непосредственным
вычислениям убеждаемся, что данные
фун-ии образуют фунд. Си-му решений
ура-ия 1.25.
Тогда общее решение исходного ура-ия
1.25
имеет вид
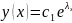 +…+
+…+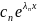 (5.25),
где
(5.25),
где
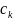 – есть произвольная постоянная.
– есть произвольная постоянная.
Пусть
все корни харак. Ура-ия различны, но
среди них есть комплексные. Тогда с
учетом того, что коэфф-ты хар. ура-ия
вещественны, приходим к выводу, что
комплексные корни входят парами вида:
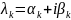 ,
,
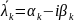 .
Для комплексного корня
.
Для комплексного корня
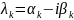 ,комплексно
значную фу-ию вещественного аргумента
,комплексно
значную фу-ию вещественного аргумента
 (6.25).
Непосредственной проверкой убеждается,
что данная фу-ия является решением ур-ия
(1.25). Аналогичным образом приходим к
выводу, что фу-ия
(6.25).
Непосредственной проверкой убеждается,
что данная фу-ия является решением ур-ия
(1.25). Аналогичным образом приходим к
выводу, что фу-ия
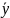 =
=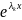 (7.25) также является решением ур-ия (1.25).
Решение однородного ур-ия (1.25)
обладают свойством линейности, поэтому
вещественные фу-ии
(7.25) также является решением ур-ия (1.25).
Решение однородного ур-ия (1.25)
обладают свойством линейности, поэтому
вещественные фу-ии
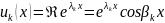 ,
(9.25)
,
(9.25)
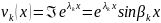
Так
как частная
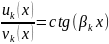 ,
то данное решение является линейно-незав.
Таким образом мы получили m-пар
комплексно-сопряженных корней
,
то данное решение является линейно-незав.
Таким образом мы получили m-пар
комплексно-сопряженных корней
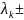
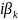 ,
,
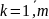 хар. ур-ия 4.25
и n-2m
различных вещественных корней
хар. ур-ия 4.25
и n-2m
различных вещественных корней
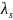 ,
,
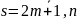 данного хар. ур-ия. Таким образом лбщее
решение исходного ур-ия имеет вид
данного хар. ур-ия. Таким образом лбщее
решение исходного ур-ия имеет вид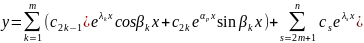 (10.25)
(10.25)
Рассмотрим теперь случай кратных корней хар. ур-ия. Непосредственными вычислениями на основании мат. индукции можно получить формулу сдвига
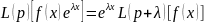 (11.25).
(11.25).
В
частности, когда многочлен L(p)
представляет собой степень
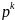 :
:
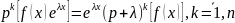 (12.25)
(12.25)
Рассмотрим сначало случай, когда λ есть веще-ый корень кратности k хар. ура-ия. Тогда имеет место цепочка соотношений:
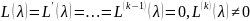
Покажем, что ему соответствует ровно k линейно независимых решений.
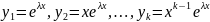
Подставим данный k-решений в ура-ие 2.25 и применим формулу сдвига 11.25. В результате получаем соотношение
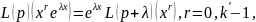 (13.25)
(13.25)
Где
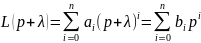 (14.25).
(14.25).
Полагая,
что в полученной формуле р=0 получаем,
что
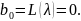
Далее последовательно дифференцируя по р соотношение 14.25 и полагая, получим соотношение р=0, получаем след. формулы
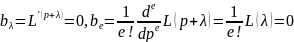
Тогда,
на основании формулы 14.25
получаем, что
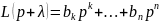 .
Так как r<k
отсюда следует
.
Так как r<k
отсюда следует
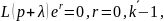
В
итоге, из соотношения 13.25
получаем, что
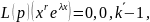
Это
означает, что фу-ия
является решением ура-ия 2.25
В итоге приходим к выводу, что каждому
вещественному корню
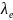 кратности
кратности
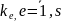 линейно независимых частных решений
исходного д.у. и при этом
линейно независимых частных решений
исходного д.у. и при этом
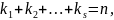 таким образом мы получаем на основании
данных корня равно n-функций,
образующих фундаментальную си-му решений
ура-ия 2.25. Поэтому в данном случае общее
решение исходног д.у. имеет вид.
таким образом мы получаем на основании
данных корня равно n-функций,
образующих фундаментальную си-му решений
ура-ия 2.25. Поэтому в данном случае общее
решение исходног д.у. имеет вид.
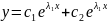 +
…+
+
…+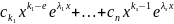 .
.
