
- •22. Линейные однородные уравнения в частных производных 1-го порядка.
- •23.Квазилинейное уравнение в частных производных 1-го порядка.
- •24.Уравнение Пфаффа.
- •25. Линейные дифференциальные уравнения порядка n с переменными коэффициентами
- •26. Линейные однородные д.У. Порядка n.
- •27.Линейные неоднородные уравнения порядка n.
- •28. Линейные однородные дифференциальные уравнения n порядка с постоянными коэффициентами.
- •29. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами и правой частью специального вида
- •30.Линейные однородные системы дифф.Ур.
- •31.Линейные неоднородные системы дифф. Ур.
- •32.Линейные однородные системы с постоянными коэффициентами.
- •33.Линейные неоднородные системы с постоянными коэффициентами и правой частью специального вида.
- •34. Линейные однородные системы с периодическими коэффициентами.
- •35.Устойчивость дифференциальных систем.
- •36.Метод функции Ляпунова.
- •37.Автономные системы.
- •38.Автономные системы на плоскости.
- •11. Интегрирующий множитель
22. Линейные однородные уравнения в частных производных 1-го порядка.
Опр.1: Линейным неоднородным дифф. ур. 1-го порядка с частными производными будем назыв. уравнение вида
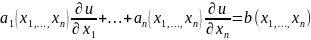 ,
(1)
,
(1)
Где
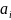 ,
b – есть заданные гладкие функции n
переменных
,
b – есть заданные гладкие функции n
переменных
 в области
в области
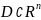 ,
u
– искомая функция.
,
u
– искомая функция.
Опр.2:
При
 в области G
уравнение (1) назыв. линейным однородным
дифф.ур. 1-го порядка с частными
производными:
в области G
уравнение (1) назыв. линейным однородным
дифф.ур. 1-го порядка с частными
производными:
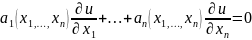 (2).
(2).
Опр.3:Решением
дифф.ур-й (1) и (2) в области D
будем назыв.гладкую в области D
функцию, которая обращает это уравнение
в равенство в каждой точке
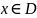 .
.
Подставим в соответствие однородному уравнению (2) систему обыкновенных дифф.ур-й:
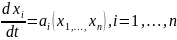 (3).
(3).
Так
как
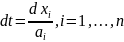 ,
то систему (3) можно представить в
симметрической форме:
,
то систему (3) можно представить в
симметрической форме:
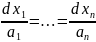 (4)
(4)
Опр.4:Систему (3) будем назыв.системой уравнений характеристик для однородного дифф.ур. (2), а её фазовые траектории – характеристикой.
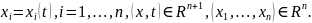
Т.1:Функция
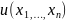 является решением однородной системы
(2) в области D
тогда и только тогда, когда она есть
первый интеграл системы характеристик
(3).
является решением однородной системы
(2) в области D
тогда и только тогда, когда она есть
первый интеграл системы характеристик
(3).
23.Квазилинейное уравнение в частных производных 1-го порядка.
Опр.5,20
Квазилинейным диф. уравнением 1-го
порядка с частными производными будем
называть уравнение
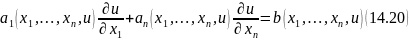 ,
,
где
и
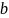 есть функции гладкие в некоторой области
есть функции гладкие в некоторой области
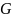 из
из
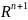 .
.
Процесс нахождения общего решения д.у. (14.20) аналогичен нахождению общего решения неоднородного д.у. 1.20. Сначала строим систему уравнений характеристик в виде:
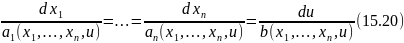
Интегральные
кривые этой системы называют
характеристиками квазилинейного д.у
(14.20), если в области G
найдены
n
независимых первых интегралах
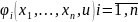 ,
то все решения д.у. (14.20) можно получить
из формулы
,
то все решения д.у. (14.20) можно получить
из формулы
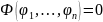 (13).
(13).
Постановка задачи Коши для квазилинейного уравнения (14.20) аналогично постановке этой задачи для однородного уравнения , при практическом решении задачи Коши будем использовать следующий алгоритм
Пусть
решение
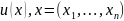 д.у (14.20) удовлетворяет условию
д.у (14.20) удовлетворяет условию
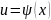 на поверхности S
заданным уравнением
на поверхности S
заданным уравнением
 .
.
Сначала
находим первые интегралы
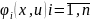 системы уравнений характеристик (15.20)
при этом мы рассматриваем интегралы
независимые в области G.
Далее исключаем из системы уравнений
системы уравнений характеристик (15.20)
при этом мы рассматриваем интегралы
независимые в области G.
Далее исключаем из системы уравнений
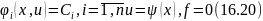
Переменные
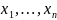 ,u.
В результате получаем равенство вида
,u.
В результате получаем равенство вида
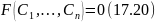
В
соотношении (17.20) подставляем выражение
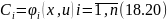
В
результате получаем решение исходного
уравнения в неявном виде
 .
.
24.Уравнение Пфаффа.
Уравнение
Пфаффа(П)
представляет собой обобщение д.у.первого
порядка в симметрической форме и в
трехмерном случае имеет вид
P(x,y,z)dx+Q(х,у,z)dу+R(х,у,z)dz=0
(1),где
Р,Q,R
есть некоторые функции, гладкие по своим
аргументам в области G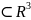 .
.
Интегралом уравнения П(1) будем наз.такую зависимость переменных х,у,z при которой дифференциалы dx,dy,dz обращают уравнение (1) в тождество на области G.Если указанная зависимость представима в виде:u(х,у,z)=0(или в параметрическом виде х=х(u,v),у=у(u,v),z=z(u,v)),то ее будем наз.двумерным интегралом или интегральной поверхностью ур.П(1).Если же интеграл ур.П представим в виде:u(х,у,z)=0,v(х,у,z)=0(или в параметрическом виде х=х(t),у=у(t),z=z(t)),то такую зависимость между переменными х,у,z будем наз.одномерным интегралом или интегральной кривой(1).
Рассмотрим
в пр-ве Охуz
векторное поле (P(x,y,z),Q(х,у,z),
R(х,у,z))=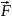 (х,у,z).Если
двумерный или одномерный интеграл
ур.(1)
задан векторным ур.:
(х,у,z).Если
двумерный или одномерный интеграл
ур.(1)
задан векторным ур.: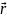 =
(х,у,z)=х
=
(х,у,z)=х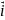 +у
+у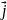 +z
+z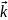 ,то
имеет место соотношение:d
=
,то
имеет место соотношение:d
=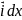 +
+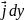 +
+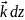 .Здесь
dx,dy,dz
в силу определения интеграла ур.П
вычислены с учетом существующей
зависимости между переменными
х,у,z.Поэтому
ур.П(1)
можно записать в следующей векторной
форме :
(х,у,z)
.Здесь
dx,dy,dz
в силу определения интеграла ур.П
вычислены с учетом существующей
зависимости между переменными
х,у,z.Поэтому
ур.П(1)
можно записать в следующей векторной
форме :
(х,у,z)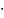 d
(х,у,z)=0.
(2).Исходя
из геометрического смысла равенство
нулю скалярного произведения 2 векторов,
приходим к выводу,что если П
есть
интегральная поверхность ур.(2),то
векторное поле F
в каждой точке этой пов-сти
ортогональна,касательной плоскости
поверхности П
в данный точке.Таким образом пов-сть П
есть
нормальная пов-сть характер.поля
F.Аналогическим
образом приходим к выводу, что есть
L-интегральная
кривая ур.П(1),то
в каждой точке этой линии векторное
поле F
ортогонально касательной линии кривой
L
данной
точки.Для векторного поля F
введем вспомогательное векторное поле
образованное с помощью определителя
третьего порядка: rоt
=
d
(х,у,z)=0.
(2).Исходя
из геометрического смысла равенство
нулю скалярного произведения 2 векторов,
приходим к выводу,что если П
есть
интегральная поверхность ур.(2),то
векторное поле F
в каждой точке этой пов-сти
ортогональна,касательной плоскости
поверхности П
в данный точке.Таким образом пов-сть П
есть
нормальная пов-сть характер.поля
F.Аналогическим
образом приходим к выводу, что есть
L-интегральная
кривая ур.П(1),то
в каждой точке этой линии векторное
поле F
ортогонально касательной линии кривой
L
данной
точки.Для векторного поля F
введем вспомогательное векторное поле
образованное с помощью определителя
третьего порядка: rоt
=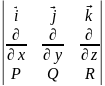 ,данное
векторное поле будем наз.ротором
векторного поля
,данное
векторное поле будем наз.ротором
векторного поля
Т.1.Условие
rоt
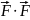 =0,
=0,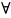 (х,у,z)
(х,у,z)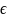 G(3)
является необходимым для существования
двумерных интегралов ур.П(1)
в
области G.
G(3)
является необходимым для существования
двумерных интегралов ур.П(1)
в
области G.
В
координатной форме ур.П
имеет вид: P(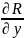 -
-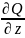 )+Q(
)+Q(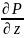 -
-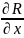 )+R(
)+R(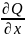 -
-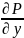 )=0(4).
)=0(4).
