31.Линейные неоднородные системы дифф. Ур.

Рассмотрим линейную неоднородную систему

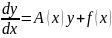(1) , где A(x)-квадратная непрерывная на [α;β] матрица порядка n; f(x)- непрерывная на [α;β] вектор функция порядка n.

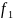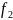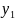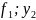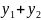Принцип суперпозиции для линейной системы (1): Пусть вектор функции f(x)= (x)+ (x), -решение системы (1) при f= -решение системы (1) при f= , то y= - решение системы (1).

Т.1:Пусть 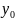-некоторое частое решение системы (1),Ф(x)- фундаментальная матрица линейной системы

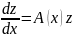(2). Тогда все решения системы (1) задаются формулой 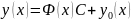, где C-вектор столбец составленный из произвольных постоянных.

Формула наз. общим решением системы (1).

Если частное решение 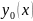системы (1) неизвестно, а известна лишь фундаментальная матрица системы (2), то лин. неоднор. система (1) может быть решена в квадратурах. В этом случае общее решение системы(1) находится методом вариации постоянных (методом Лагранжа).

Т2: Если Ф(x) –фундаментальная матрица системы (2), то общее решение системы (1) задаётся

.

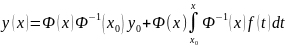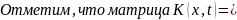
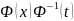явл. матрицантом системы (1), удовлетворяющим начальным условиям K(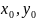 )=I, I-единичная матрица.

32.Линейные однородные системы с постоянными коэффициентами.

Рассмотрим нормальную линейную однородную дифф.систему n-го порядка 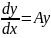(1), где A- постоянная квадратная матрица порядка n. Ясно, что система (1) всегда имеет тривиальное (нулевое) решение y=0.

Будем искать нетривиальные решения системы (1) в виде 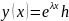(2), где 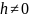– числовой вектор-столбец размера n.

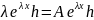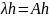Подставляя функцию (2) в систему (1) получаем, что или (3).

Лемма 1:Для того, чтобы вектор-функция (2) была нетривиальным решением системы (1) необходимо и достаточно, чтобы λ было собственным значением, а h – соответствующим ему собственным вектором линейного однородного отображения Ay, .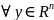

Ур. (3) перепишем в виде 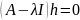. Оно имеет нетривиальное решение тогда и только тогда, когда определитель 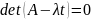(4) –характеристическое уравнение системы (1).

Рассмотрим случай, когда все корни 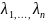характер.ур. (4) вещественны и различны.

Выберем из них корень 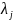и подставим его в уравнение (3). В результате получим систему лин.однор.ур-й с определителем равным нулю.

Среди решений этой системы есть ненулевые и данное решение и данное решение является собственным вектором 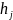матрицы А системы(1). Выбранному вектору соответствует такое частное решение системы (1) .

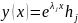Так как все корни характер.ур. (4) вещественны и различны получаем n вектор-функций 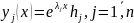, которые образуют ФСР однородной системы (1). Поэтому общее решение системы (1) имеет вид 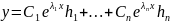(5), где -постоянные параметры.

Пусть среди простых корней характер.ур.системы (1) есть комплексные. Они делятся на пары комплексно сопряженных корней 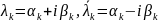. Каждому комплексному корню соответствует комплексное решение системы (3) в виде 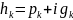, где векторы 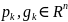для полученных комплексных характеристических корней 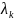и собственных векторов .

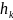Рассмотрим комплекснозначную вектор-функцию .

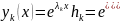Значит функции 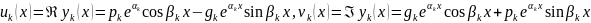(6) являются решениями системы (1).

На основании вещественных частных решений вида 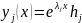и (6) строим ФСР линейной системы (1). Далее на основании данной ФСР получаем общее решение системы (1).