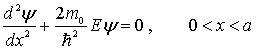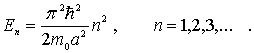- •1)Электромагнитная природа света.Световые волны.Волновое уравнение и простейшие модели световых волн, вытекающие из уравнений максвелла: плоская бегущая волна,сферическая волна.
- •2) Основные характеристики плоских монохроматических волн: фазовая скорость, плотность энергии, интенсивность, поляризация.
- •4) Понятие о временной и пространственной когерентности световых волн.
- •5)Интерференция света: условия и способы наблюдения (опыт юнга, интерферометр майкельсона, интерференция при отражении от тонких пленок).
- •6) Дифракция света: принцип гюйгенса-френеля, дифракция френеля, дифракция фраунгофера.
- •7) Дифракционная решетка.Понятие о голографии.
- •[Править]Формулы
- •7А)явление обращения волного фронта. Понятие об адаптивной оптике.
- •[Править]Методы обращения волнового фронта
- •Вопрос 8. Явление дисперсии и поглощения волн. Понятие о молекулярном рассеянии света.
- •Вопрос 10. Поляризация света.
- •Вопрос 11. Тепловое излучение в замкнутой полости. Закон Кирхгофа. Закон Стефана Больцмана и Вина. Формула Планка.
- •Вопрос 12. Понятие фотона. Фотоэффект и эффект Комптона. Давление света.
- •13)Физические предпосылки возникновения квантовой механики(проблемы не разрешимые классической физикой).Постулаты бора.
- •14)Волны де-бройля.Соотношение неопределенностей гейзенберга. Во́лны де Бро́йля — волны, связанные с любыми микрочастицами и отражающие их волновую природу. Физический смысл
- •Вопрос 15. Постулаты квантовой механики.
- •Получение уравнения Шрёдингера предельным переходом [источник не указан 56 дней]
- •Вопрос 17. Операторы важнейших физических величин: оператор импульса, проекции момента импульса, оператор квадрата момента импульса. Законы сохранения в квантовой физики.
- •Вопрос 18. Квантование момента импульса. Опыт Штерна-Герлаха. Спин.
- •Вопрос 19. Квантомеханическое движение частицы в бесконечно глубокой прямоугольной потенциальной яме.
- •Вопрос 20. Прохождение частиц через потенциальный барьер ( туннельный эффект).
- •Вопрос 21. Квантовый гармонический осциллятор.
- •Вопрос 22. Квантомеханическое описание атома водорода.
- •Вопрос 23. Принцип тождественных частиц. Принцип Паули. Фермионы и бозоны.
Вопрос 19. Квантомеханическое движение частицы в бесконечно глубокой прямоугольной потенциальной яме.
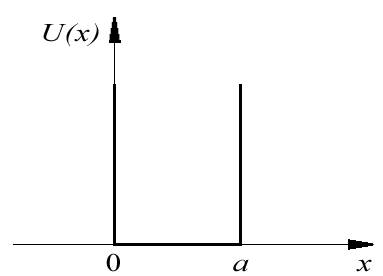
Рассмотрение стационарных задач квантовой механики начнем с наиболее простой для анализа задачи - о движении частицы в потенциальной яме с непроницаемыми, т.е. бесконечно высокими стенками. Такие ямы называют еще потенциальными ящиками, наиболее часто это название применяется по отношению к трехмерной потенциальной яме. Выявленные при этом особенности движения, такие, например, как квантование энергии, вырождение энергетических уровней и т.д. в дальнейшем будут проанализированы для случая ямы конечной глубины.
Одномерная
потенциальная яма. Рассмотрим
частицу, находящуюся в одномерной
прямоугольной потенциальной яме с
бесконечно высокими стенками. В этом
случае потенциальная энергия
частицы ![]() имеет
вид
имеет
вид
![]()
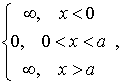
т.е.
внутри ямы (![]() )
потенциальная энергия
)
потенциальная энергия ![]() постоянна
и равна нулю, а вне ямы обращается в
бесконечность ( рис.4.1 ).
постоянна
и равна нулю, а вне ямы обращается в
бесконечность ( рис.4.1 ).
|
Рис. 4.1. |
Запишем уравнение Шредингера для одномерного движения частицы вдоль оси
|
(4.11) |
Поскольку
вне ямы потенциальная энергия обращается
в бесконечность, то для того, чтобы
выполнялось уравнение (4.11) ,
необходимо, чтобы вне ямы волновая
функция ![]() обращалась
в ноль, т.е.
обращалась
в ноль, т.е. ![]() .
Это означает, что в случае ямы с бесконечно
высокими стенками частица не может
выйти за пределы ямы, поскольку такие
стенки являются непроницаемыми для
частицы. В силу непрерывности волновая
функция
должна
обращаться в нуль и на границах ямы:
при
.
Это означает, что в случае ямы с бесконечно
высокими стенками частица не может
выйти за пределы ямы, поскольку такие
стенки являются непроницаемыми для
частицы. В силу непрерывности волновая
функция
должна
обращаться в нуль и на границах ямы:
при ![]() и
при
и
при ![]() .
.
Таким образом, задача о движении частицы в яме сводится к решению уравнения
|
(4.12) |
с граничными условиями
![]()
Введем обозначение
|
(4.13) |
При этом уравнение (4.12) принимает вид хорошо известного из теории колебаний уравнения
![]()
решение которого есть
|
(4.14) |
Используя
граничное условие ![]() ,
получаем
,
получаем
![]()
откуда
следует, что ![]() ,
где
,
где ![]() .
Отметим, что при четных значениях
.
Отметим, что при четных значениях ![]() и
при
и
при ![]()
![]() ,
а при нечетных значениях
,
а при нечетных значениях
![]() .
Однако, физический смысл имеет не сама
волновая функция
,
а квадрат ее модуля
.
Однако, физический смысл имеет не сама
волновая функция
,
а квадрат ее модуля ![]() ,
который от выбора значения
,
т.е. от знака
не
зависит. Поэтому без потери общности
можно считать, что
,
который от выбора значения
,
т.е. от знака
не
зависит. Поэтому без потери общности
можно считать, что ![]() .
.
Второе
граничное условие ![]() приводит
к соотношению
приводит
к соотношению
![]()
которое
для ![]() выполняется
при
выполняется
при
|
(4.15) |
Отметим,
что значение ![]() ,
формально также входящее в решение (4.14) ,
не удовлетворяет условию задачи, т.к.
при этом
,
формально также входящее в решение (4.14) ,
не удовлетворяет условию задачи, т.к.
при этом ![]() ,
что означает, что частица в яме отсутствует.
Поэтому значение
следует
отбросить.
,
что означает, что частица в яме отсутствует.
Поэтому значение
следует
отбросить.
Подставляя (4.13) в (4.15) , приходим к выражению для полной энергии частицы, движущейся в потенциальной яме с непроницаемыми стенками
|
(4.16) |
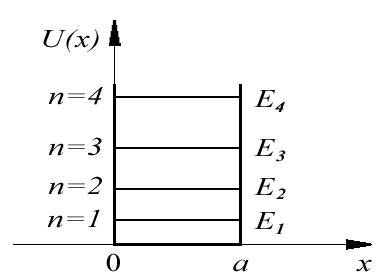
Важной особенностью полученного энергетического спектра (4.16) является его дискретность. Частица, находящаяся в потенциальной яме, может иметь только дискретные, квантованные, значения энергии, определяемые выражением (4.16) (см.рис.4.2) . Отметим, что решение
|
Рис. 4.2. |
уравнения Шредингера само по себе к квантованию энергии не приводит, квантование возникает из-за граничных условий, накладываемых на волновую функцию, т.е. из-за равенства нулю волновой функции на границе потенциальной ямы.
Число
в (4.16) ,
определяющее энергию частицы в яме,
называется квантовым
числом, а
соответствующее ему значение ![]() -
уровнем энергии. Состояние частицы с
наименьшей энергией, в данном случае
с
-
уровнем энергии. Состояние частицы с
наименьшей энергией, в данном случае
с ![]() ,
называется основным
состоянием.
Все остальные состояния являются возбужденными:
значение
,
называется основным
состоянием.
Все остальные состояния являются возбужденными:
значение ![]() отвечает
первому возбужденному состоянию,
значение
отвечает
первому возбужденному состоянию,
значение ![]() -
второму возбужденному состоянию и т.д.
-
второму возбужденному состоянию и т.д.