Вопрос 15. Постулаты квантовой механики.

Постулат №1. 

Состояние частицы (или системы частиц) задано, если известна волновая функция Y(q)

 Постулат №2. 

Волновые функции подчиняются принципу суперпозиции: если в состоянии с волновой функцией Y₁(q) некоторое измерение приводит к результату Х₁, а в состоянии Y₂(q) - к результату Х₂, то всякая функция вида Y=с₁Y₁(q)+с₂Y₂(q)

описывает такое состояние, в котором измерение дает либо результат Х₁, либо Х₂.

Постулат №3. 

Всякой физической величине L в квантовой механике сопоставлен линейный самосопряженный оператор. Единственно возможными величинами, которые может иметь эта физическая величина, являются собственные значения l операторного уравнения LY=lY

 Постулат №4.

Возможная волновая функция состояния системы Y получается при решении дифференциального уравнения ih·dY/dt=HY, где H - оператор Гамильтона, а уравнение называется уравнением Шредингера.

Постулат №5. 

Если произвести многократные измерения какой-либо динамической переменной l системы, находящейся в состоянии Y, то на основании результатов этих измерений можно определить ее среднюю величину. Эта средняя величина вычисляется по формуле:

l=òY^*LYdq/òY^*Ydq

Уравнение Шредингера

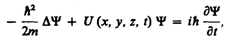
Получение уравнения Шрёдингера предельным переходом [источник не указан 56 дней]

Существует способ ^{[источник не указан 56 дней]} получить уравнение Шрёдингера, используя предельный переход к классической механике.

Рассмотрим оператор

Поскольку интеграл , взятый по всему пространству, есть величина постоянная (для нормированной функции равная 1) то:

(Звездочкой будем обозначать комплексное сопряжение) Подставляя сюда наш оператор (оператор со звездочкой — комплексно сопряженный, с тильдой — транспонированный):

Иначе:

Поскольку это равенство должно выполняться для произвольной функции , то отсюда следует, что тождественно , то есть оператор эрмитов. Чтобы выяснить смысл этого оператора, подействуем им на функцию (функция квазиклассической системы,  — медленно меняющаяся функция, -действие):

Пренебрегая первым членом в силу его малости получаем:

То есть  — собственное значение нашего оператора. Но эта производная есть не что иное, как классическая энергия системы (функция Гамильтона). Поэтому этот оператор называют гамильтонианом или гамильтоновым оператором.

Мы не будем здесь приводить вывод оператора импульса (точнее, оператора величины, сохраняющейся в силу однородности пространства), приведем лишь результат:

Или в компонентах (оси …):

В том, что это есть оператор величины переходящей в классический импульс можно убедиться, тем же методом, что был предложен для гамильтониана. Можно показать, что сохраняющаяся со временем величина, в частности импульс, измерима одновременно с энергией. Поэтому мы предположим, что соотношение между операторами импульса и энергии совпадает с классическим соотношением между соответствующими величинами:

Но:

Таким образом:

Вопрос 17. Операторы важнейших физических величин: оператор импульса, проекции момента импульса, оператор квадрата момента импульса. Законы сохранения в квантовой физики.

Как, зная волновую функцию предсказать результат измерения соответствующей физической величины у частицы, находящейся в рассматриваемом квантовом состоянии? Для получения информации о физических величинах, связанных с движущейся частицей, в квантовой механике разработан специальный математический аппарат, который использует представления об операторах физических величин и результатах их действия на волновые функции.

      В работах М.Борна, П.Дирака и др. был сформулирован второй постулат квантовой механики, утверждающий, что каждой физической величине соответствует определенный оператор этой физической величины. При этом соотношения между операторами в квантовой механике имеют ту же структуру, что и соотношения между соответствующими им физическими величинами в классической механике.

      Для расшифровки этого постулата дадим некоторые пояснения. Оператор - это математическое правило, следуя которому мы можем преобразовать одну функцию в другую. Задать оператор - это означает определить рецепт такого преобразования. Такое преобразование может быть простым умножением исходной функции на число или известную функцию, дифференцированием функции, перестановкой аргументов функции и др.

      В квантовой механике в качестве символа соответствующего оператора используется классическое обозначение физической величины, ставя над буквой "шляпку" в виде значка " ". Например,  - это оператор координаты  ,   - оператор проекции импульса на ось  ,  - оператор потенциальной энергии и т.д. Оператор предполагается действующим на написанную вслед за ним функцию. В качестве таких функций в квантовой механике выступают волновые функции. При этом равенство двух функций   в операторной форме будет записываться как равенство операторов:  .

      Определим операторы основных физических величин в квантовой механике.

      1. Оператор координаты. Действие этого оператора на волновую функцию сводится к умножению ее на соответствующую координату, то есть.

     

.

(3.27)

     В символической операторной форме записи этих операций имеют вид

     

.

(3.28)

      Объединяя эти формулы, можно ввести векторный оператор  , соответствующий радиусу-вектору   в классической механике. Такой оператор формально рассматривается как некоторый вектор, имеющий в качестве компонент в декартовой системе координат операторы  . Поэтому

     

.

(3.29)

      2. Оператор импульса. С помощью операций дифференцирования по координатам определим операторы проекций импульса, записав эти определения в символической операторной форме как

     

.

(3.30)

      Все три формулы в (3.30) можно объединить в одну, введя векторный оператор импульса  , который с учетом (3.30) запишется как

     

.

(3.31)

     Здесь

     

.

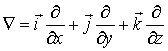      Используя соотношение классической механики

     

,

     определим оператор квадрата импульса как

     

.

(3.32)

     Используя символ оператора Лапласа, запишем (3.32) в более компактном виде

     

.

(3.33)

      3. Оператор момента импульса. По формуле классической механики, определяющей момент импульса частицы как вектор  , запишем выражения для его проекций на координатные оси:

     

.

      Эти соотношения превратим в операторные, определяющие операторы проекций момента импульса

     

.

(3.34)

     Оператор квадрата момента импульса можно построить по правилу

     

.

(3.35)

      Отметим, что задачи квантовой механики, обладающие сферической симметрией, удобнее решать не в декартовой, а в сферической системе координат  ,   и  . Переходя от декартовых координат к сферическим по обычным правилам замены переменных  ,  ,  , формулы (3.34) и (3.35) можно преобразовать к следующему виду

     

.

(3.36)

     Здесь

     

     - угловая часть оператора Лапласа в сферической системе координат.

      4. Операторы энергий. Классическая формула связи кинетической энергии частицы с квадратом ее импульса

     

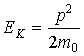
     позволяет записать аналогичное соотношение между соответствующими операторами. Поэтому

     

.

(3.37)

      Если частица движется в стационарном силовом поле, и ее потенциальная энергия   определена в любой точке пространства, то оператор потенциальной энергии  определяется как оператор умножения на функцию  , то есть

     

.

(3.38)

      Так как полная энергия частицы в классической механике есть сумма кинетической и потенциальной энергий, то в квантовой механике оператор полной энергии   определяется как сумма операторов кинетической и потенциальной энергий. Поэтому

     

.

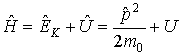     Раскрывая выражение для оператора квадрата импульса по формуле (3.33), запишем оператор полной энергии как

     

.

(3.39)

     В классической механике полную энергию частицы, выраженную через ее координаты и импульс, называют функцией Гамильтона. Поэтому в квантовой механике оператор полной энергии   называют оператором функции Гамильтона или просто гамильтонианом.

      Гамильтониан   является основным оператором квантовой механики, поскольку, выбирая конкретный вид гамильтониана, с учетом силового поля, действующего на частицу, мы формулируем на математическом языке все особенности квантовой системы. Поэтому и основное уравнение нерелятивистской квантовой механики - уравнение Шредингера (3.8) может быть записано в операторной форме

     

,

(3.40)

     содержащей гамильтониан  .

      Физическое содержание операторного метода в квантовой механике накладывает определенные ограничения на возможный вид квантовомеханических операторов. Пусть  - оператор физической величины  . Тогда для любых функций   и   и произвольных постоянных   и   должно выполняться равенство

     

.

(3.41)

      Операторы, обладающие таким свойством, называются линейными операторами. Свойство линейности операторов физических величин тесно связано с принципом суперпозиции квантовых состояний. Только использование в теории линейных операторов не нарушает этого принципа.

      Оператором физической величины может быть только линейный самосопряженный (эрмитов) оператор. Только такому оператору соответствует действительная (не комплексная) физическая величина. Самосопряженным называют оператор, который совпадает со своим сопряженным оператором. В этом случае для произвольных функций   и  тождественно выполняется следующее интегральное равенство

     

.

(3.42)

      Таким образом, каждой физической величине в квантовой механике приводится в соответствие определенный линейный самосопряженный оператор. Непосредственной проверкой можно убедиться, что все приведенные выше квантовомеханические операторы обладают такими свойствами.

Законы сохранения в квантовой физики.

В квантовой механике также возможно формулирование закона сохранения энергии для изолированной системы. Так, в шредингеровском представлении при отсутствии внешних переменных полей гамильтониан системы не зависит от времени и можно показать^[13], что волновая функция, отвечающая решению уравнения Шредингера, может быть представлена в виде:

Здесь   — волновая функция системы,   — совокупность переменных, от которых зависит состояние системы в данном представлении,   —собственные функции и собственные значения оператора Гамильтона,   — постоянная Планка,   — некоторые постоянные комплексные коэффициенты, характеризующие состояние системы. По определению средней энергией квантовой системы, описываемой волновой функцией, называется интеграл

где   — гамильтониан системы. Несложно видеть, что этот интеграл не зависит от времени:

где также использовано свойство ортонормированности собственных функций гамильтониана^[14]. Таким образом, энергия замкнутой системы сохраняется.

Следует, однако, отметить, что по сравнению с классической механикой у квантового закона сохранения энергии имеется одно существенное отличие. Дело в том, что для экспериментальной проверки выполнения закона необходимо провести измерение, представляющее собой взаимодействие исследуемой системы с неким прибором. В процессе измерения система, вообще говоря, более не является изолированной и её энергия может не сохраняться (происходит обмен энергией с прибором). В рамках классической физики, однако, это влияние прибора всегда может быть сделано сколь угодно малым, в то время как в квантовой механике имеются фундаментальные ограничения на то, насколько малым может быть возмущение системы в процессе измерения. Это приводит к так называемому принципу неопределённости Гейзенберга, который в математической формулировке может быть выражен в следующем виде:

,

где   имеет смысл среднеквадратичного отклонения измеренного значения энергии от среднего значения при проведении серии измерений,   — продолжительность взаимодействия системы с прибором в каждом из измерений.

В связи с наличием этого фундаментального ограничения на точность измерений в квантовой механике часто говорят о законе сохранения средней энергии (в смысле среднего значения энергии, полученного в результате серии измерений).
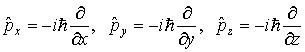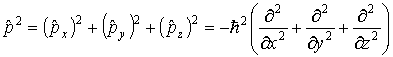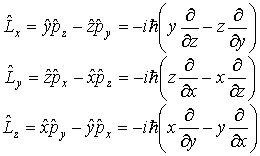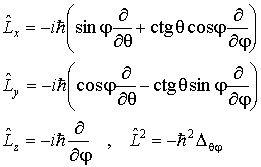