2. Использование свойства ограниченности.

Теорема 1. Если для любого х Х выполняются неравенства f (x) A,

g(x) , то на множестве Х уравнение f (x) = g (x) равносильно системе

Иными словами, если , то уравнение f (x) = g (x) на множестве Х равносильно системе

Теорема 2. Пусть требуется решить уравнение

Если на D выполняются неравенства , то на

множестве D уравнение равносильно системе

Пример № 1.

Решите уравнение

cos 2x + cos

Решение:

cos 2x + cos

Последнее уравнение есть уравнение вида f(x) =g(x),

где f(x) = cos 2x, g(x) = 2 – cos

Заметим , что f(x)=1, g(x) =1.

Следовательно, уравнение равносильно системе

х = ,

так как cos тогда и только тогда, когда k , то есть k = 5n.

Ответ: .

Пример № 2.

Решите уравнение

Решение:

Уравнение есть уравнение вида f(x) = g(x), где

f(x) = , g(x) = sin x- cos x.

Заметим, что f(x) R,

g(x) =

R.

Следовательно, уравнение равносильно системе

, так как

Z Z .

Ответ: Z .

Пример № 3.

Решите уравнение

arcsin(x (x + y)) + arcsin(y (x + y)) =

Решение:

Так как arcsin(x (x + y) ) , arcsin( y ( x+y) ) для любых пар , для которых имеет смысл левая часть уравнения , то уравнение равносильно системе

Ответ:

Пример № 4.

Решите уравнение

(1)

Решение:

Воспользуемся неравенством Коши между средним арифметическим и средним геометрическим двух неотрицательных величин:

,

,

,

(2)

Заметим, что равенство достигается тогда и только тогда, когда .

Снова воспользуемся неравенством Коши (теперь для величин ):

,

,

,

,

. (3)

Заметим, что в неравенстве (3) равенство достигается тогда и только тогда, когда

Используя неравенство (3) и учитывая возрастание функции у = 2^t , получаем

(4).

Из неравенства (2) и (4) следует, что .

Равенство достигается тогда и только тогда, когда

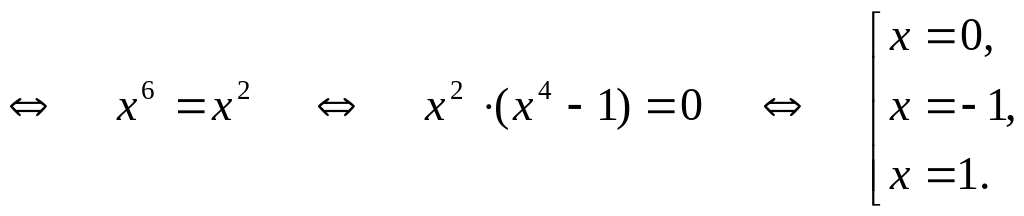
Ответ: .

Пример № 5.

Решите уравнение

(1)

Решение:

Воспользуемся неравенством Коши , справедливым для любых неотрицательных чисел a и b. Отметим, что равенство достигается тогда и только тогда, когда a=b.

Имеем

Заметим, что равенство достигается при , т. е. при х = .

1+ для любых пар значений переменных х и у, причём равенство достигается тогда и только тогда, когда =0.

Получим, что наименьшее значение левой части уравнения (1) равно 8.

Далее

для любых пар , причём равенство достигается тогда и только тогда, когда

Значит, уравнение (1) равносильно системе уравнений

Ответ: .