Комитет образования

администрации города Тамбова.

Информационно – методический центр

Методическое пособие « Использование свойств функций при решении уравнений и неравенств».

Тамбов 2007 год.

Содержание

Предисловие.

1. Использование свойства монотонности.

2. Использование свойства ограниченности.

3. Использование свойства чётности (нечётности).

4. Использование свойства выпуклости.

5. Приложения.

6. Литература.

1. Использование свойства монотонности.

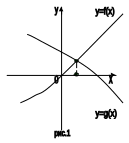
Теорема 1. Если на промежутке Х одна из функций y=f (x), y=g (x) убывает, а

другая возрастает, то на этом промежутке Х уравнение f (x) = g (x) имеет

не более одного корня, то есть либо имеет только один корень ( рис. 1),

либо вообще не имеет корней (рис. 2)

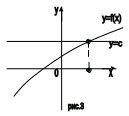
Теорема 2. Если на промежутке Х функция y = f(x) возрастает ( убывает), то

на этом промежутке Х уравнение f (x) = C , где C = const, имеет

не более одного корня, то есть либо имеет только один корень (рис.3),

либо вообще не имеет корней ( рис.4).

Пример № 1.

Решите уравнение

(*)

Решение:

Данное уравнение есть уравнение вида f(x) = g(x),

где f(x) = 2arcsin2x, g(x)=3arccos x.

f(x) возрастает на D (f), g(x) убывает на D (g). Следовательно, уравнение ( *) имеет не более одного корня.

Заметим, что х=0,5 является корнем уравнения (*).

Ответ:

Пример № 2.

Решите уравнение

Решение:

ОДЗ : х .

Уравнение равносильно уравнению

( в процессе равносильных преобразований мы воспользовались свойством , справедливым при ).

Положим , тогда . Последнее уравнение принимает вид

Полученное уравнение есть уравнение вида f(y) = c, где f(y) = ,с=1.

Так как f убывает на R, то уравнение имеет не более одного корня. Заметим, что у = 1 корень этого уравнения.

Окончательно,

Ответ: .

Пример № 3.

Решите уравнение:

х^х =

Решение:

ОДЗ : х .

Данное уравнение есть уравнение вида f(x) = c, где f ( x) =x^x, c = .

Исследуем функцию f на монотонность.

.

.

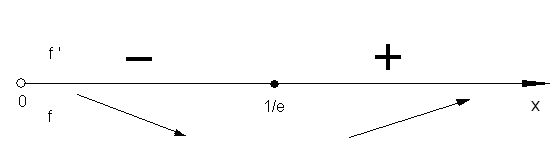
На промежутке функция f (x )= x^x убывает

Следовательно, на уравнение имеет не более одного корня.

Заметим, что х = ( ) является корнем уравнения , так как

(

На промежутке функция f возрастает.

Следовательно, на уравнение имеет не более одного корня.

Заметим, что х = является корнем уравнения , так как

Ответ : .

Пример № 4.

Найдите количество корней уравнения (1).

Решение.

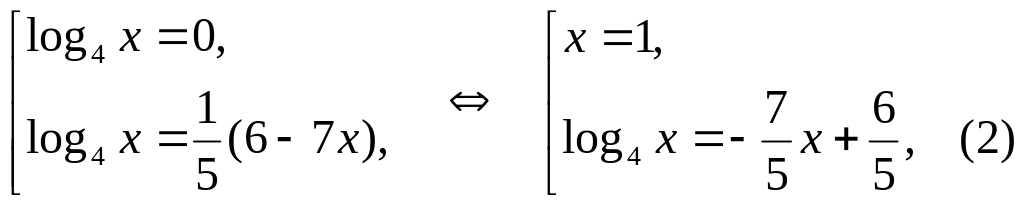
( 2 )

Уравнение ( 2 ) есть уравнение вида f (x) = g(x), где

f ( x ) = возрастает на ,

g (x) = убывает на .

Следовательно, уравнение (2) имеет не более одного корня. Покажем, что уравнение (2) имеет единственный корень, не равный 1.

= .

Рассмотрим функцию р(х) = непрерывную на .

Находим

р ( ) =

р (1) =

Так как на отрезке функция р непрерывна и на концах отрезка принимает значения разных знаков , то существует такое х₀ , что р(х₀)=0, т.е. х₀ является корнем уравнения (2).

Ответ: 2 корня.

Пример № 5.

Решите неравенство

2 х⁹ – х⁵ + х 2.

Решение:

Найдём промежутки возрастания и убывания функции f (x) = 2 х⁹ – х⁵ + х – 2.

Так как дискриминант квадратного трёхчлена 18 у² – 5у+1 является отрицательным числом и коэффициент при у² этого квадратного трёхчлена больше нуля, то для каждого действительного х имеем неравенство

Таким образом, функция у = f (x) является непрерывной и возрастающей на всей числовой прямой, поэтому её график может пересекать ось ОХ только в одной точке.

Учитывая, что f (1) = 0, заключаем, что множеством решений данного неравенства является промежуток .

Ответ: .