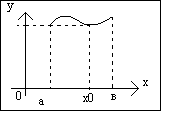
- •1. Задача, о площади криволинейной трапеции приводящая к понятию определенного интеграла.
- •2. Классы интегрируемых функций.
- •3. Теорема об определенном интеграле с переменным верхним пределом
- •4. Теорема Лейбница – Ньютона.
- •5. Теорема об интегрировании по частям
- •6. Теорема о замене переменной в определенном интеграле
- •7. Вывод формулы вычисления площади плоской фигуры (в декартовой системе координат)
- •8. Вывод формулы вычисления длины дуги (в декартовой системе координат)
- •9. Вывод формулы вычисления объема тела вращения относительно оси ox и oy (в декартовой системе координат).
- •10. Теорема об абсолютной сходимости несобственного интеграла 1-го рода
- •11. Сформулируйте и докажите свойства решений олду.
- •12. Теорема о равенстве нулю вронскиана линейно-зависимых функций (необх. Усл. Л.З.).
- •13. Теорема о структуре общего решения лоду
- •14. Теорема о структуре общего решения лнду
- •15. Теорема о суперпозиции решений (принцип сложения решений)
- •16. Метод вариации произвольных постоянных – метод Лагранжа
- •17. Необходимый признак сходимости.
- •18. Критерий сходимости рядов с неотрицательными членами.
- •19. Предельный признак сравнения для рядов с неотрицательными членами.
- •20. Признак Даламбера.
- •21. Радикальный признак Коши.
- •22. Абсолютная и условная сходимость. Достаточный признак сходимости знакопеременных рядов.
- •23. Степенные ряды. Теорема Абеля. Радиус сходимости.
- •24.Тригонометрический ряд Фурье. Нахождение коэффициентов для четных и нечетных функций.
- •25. Нахождение коэффициентов для тригонометрического р. Фурье (теорему док).
- •1. Понятие первообразной. Свойства первообразной.
- •2. Понятие неопределенного интеграла. Свойства неопределенного интеграла.
- •3. Методы вычисления неопределенного интеграла: метод подстановки (замены переменной),
- •4.Интегрирование рациональных функций.
- •7. Интегрирование иррациональных функций.
- •9. Понятие интегральной суммы.
- •10. Понятие определённого интеграла. Геометрический смысл определенного интеграла
- •11. Необходимый признак интегрируемости функции по Риману. Функция Дирихле.
- •12. Свойства определенного интеграла. Теорема о среднем.
- •13. Свойства линейности и аддитивности определённого интеграла.
- •14. Свойства определенного интеграла, выраженные неравенствами
- •15. Интегралы с переменным верхним пределом.
- •16. Объем тела вращения с заданным поперечным сечением
- •18. Понятие несобственного интеграла II рода
- •19. 20. Признаки сравнения (для несобственного интеграла I и II рода.)
- •21. Свойства определенного интеграла от чет. И нечт. Функции на симметричном промежутке.
- •22. Понятие общего решения дифференциального уравнения первого порядка, частное решение, начальные условия, задача Коши.
- •2 3. Теорема о существовании и единственности решения ду в полных дифференциалах.
- •24. О пределитель Вронского.
- •25. Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентами. Вид частных решений, характеристическое уравнение
- •26.Теорема о существовании и единственности решения задачи Коши д.У. Порядка выше первого.
- •27. Числовой ряд. Основные понятия и определения: определение числового ряда, n-ой
- •28. Интегральный признак Коши.
- •29. Знакочередующиеся ряды. Теорема Лейбница.
- •30. Равномерная сходимость функционального ряда.
- •31. Теорема и признак Вейерштрасса:
- •32. Свойство равномерно сходящихся функциональных рядов.
- •33. Ортогональная система функций:
- •34. Теорема Дирихле. Условия Дирихле.
- •35. Степенные ряды. Область сходимости. Радиус сходимости.
- •36. Ряд Тейлора, область сходимости. Достаточный признак сходимости ряда Тейлора.
- •37. Ряды Маклорена
- •38. Тригонометрический ряд Фурье
7. Интегрирование иррациональных функций.
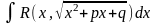 прием
выделения полного квадрата и замены
полного квадрата на новую переменную
прием
выделения полного квадрата и замены
полного квадрата на новую переменную
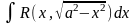 подстановка:
подстановка:

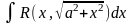 подстановка:
подстановка:
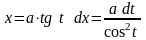
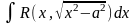 подстановка:
подстановка:
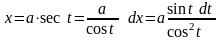
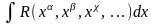 ,
где a,
b,
g
…– дробные рациональные числа.
Рационализация проводится подстановкой:
,
где a,
b,
g
…– дробные рациональные числа.
Рационализация проводится подстановкой:
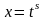 ,
где s
– наименьшее общее кратное a,
b,
g
,
где s
– наименьшее общее кратное a,
b,
g
 ,
где a,
b,
g
…– дробные рациональные числа.
Рационализация проводится подстановкой:
,
где a,
b,
g
…– дробные рациональные числа.
Рационализация проводится подстановкой:
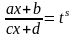 ,
где s
– наименьшее общее кратное a,
b,
g
,
где s
– наименьшее общее кратное a,
b,
g
Выражение
вида
 где (m,n,p,a,b)
– const,
называется дифференциальным
биномом,
интеграл от него решается при помощи
подстановки Чебышева.
где (m,n,p,a,b)
– const,
называется дифференциальным
биномом,
интеграл от него решается при помощи
подстановки Чебышева.
8. Интегрирование дифференциального бинома. Теорема
И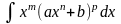 нтеграл
вида , где m,
n,
p
– рациональные числа
нтеграл
вида , где m,
n,
p
– рациональные числа
выражается через элементарные функции только в следующих случаях:
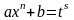
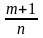 p
< 0
–
целое
Þ
x
= t
s,
d
x
= s
t
s-1
d
t
, s
–
нок
знаменателей
m
и
n;
p
< 0
–
целое
Þ
x
= t
s,
d
x
= s
t
s-1
d
t
, s
–
нок
знаменателей
m
и
n;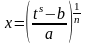 – целое
Þ
, s
–
знаменатель
дроби
– целое
Þ
, s
–
знаменатель
дроби
p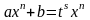
 =
к/s,
;
=
к/s,
;
– целое Þ ,
s – знаменатель дроби p= к/s,
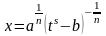
9. Понятие интегральной суммы.
Пусть на отрезке [a,b] определена вещественнозначная функция f.
Рассмотрим разбиение
отрезка ![]() —
конечное множество попарно различных
точек отрезка . Это разбиение делит
отрезок[a,b] на n отрезков
—
конечное множество попарно различных
точек отрезка . Это разбиение делит
отрезок[a,b] на n отрезков ![]() .
Длина наибольшего из отрезков
d =
max(Δxi), называется
диаметром
разбиения, где Δxi = xi − xi −
1.
.
Длина наибольшего из отрезков
d =
max(Δxi), называется
диаметром
разбиения, где Δxi = xi − xi −
1.
Отметим
на каждом отрезке разбиения по точке
![]() .
Интегральной
суммой называется
выражение
.
Интегральной
суммой называется
выражение
![]() .
.
10. Понятие определённого интеграла. Геометрический смысл определенного интеграла
Определенным
интегралом
от функции у=
на
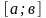 называется конечный предел соответствующей
интегральной суммы при неограниченном
увеличении числа разбиений промежутка
на части (noo)
и стремлении длин всех частичных
промежутков к нулю (хi 0)
называется конечный предел соответствующей
интегральной суммы при неограниченном
увеличении числа разбиений промежутка
на части (noo)
и стремлении длин всех частичных
промежутков к нулю (хi 0)
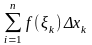 если
предел конечен и не зависит от разбиений
и выбора точки
если
предел конечен и не зависит от разбиений
и выбора точки

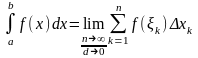 ,
где
- подынтегральная функция.
,
где
- подынтегральная функция.
 -подынтегральное
выражение.
-подынтегральное
выражение.
а- нижний предел интегрирования.
в- верхний предел интегрирования.
d- длина наибольшего из отрезков разбиения.
Геометрический
смысл интеграла
- это площадь криволинейной трапеции,
ограниченной линиями
 ,
y=0,
x=a,
x=b,
,
y=0,
x=a,
x=b,
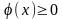 на [a,
b].
на [a,
b].

11. Необходимый признак интегрируемости функции по Риману. Функция Дирихле.
Признак
Римана (теоретически). Для существующего
определённого интеграла необходимо и
достаточно, чтобы

Функция
Дирихле — функция ![]() ,
принимающая значение 1, если аргумент
есть рациональное
число, и значение 0, если аргумент есть
иррациональное число,
,
принимающая значение 1, если аргумент
есть рациональное
число, и значение 0, если аргумент есть
иррациональное число,
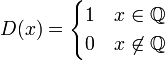 .
.
Функция Дирихле — пример функции не интегрируемой в смысле Римана.
12. Свойства определенного интеграла. Теорема о среднем.
Основные свойства определенного интеграла.
 ,
,
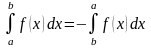
 ,
где c-const,
,
где c-const,
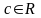
Определенный
интеграл от
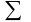 ф-ий:
ф-ий: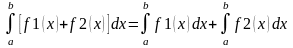
Адитивность
определенного
интеграла
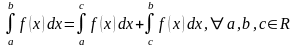
Если

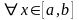 ,
то
,
то
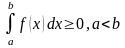
Монотонность
определенного интеграла. если
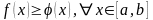 ,
то
,
то
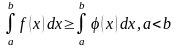
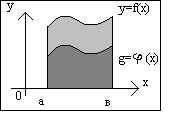
Ограниченность.
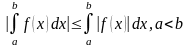
Оценка
определенного интеграла. Пусть f(х)
интегрируема на [a,b],
a<b,
,

 Теорема
о среднем:
Если f(х)
непрерывна на [a,b],
то существует точка
Теорема
о среднем:
Если f(х)
непрерывна на [a,b],
то существует точка
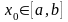 ,
такая что
,
такая что
 ,
где
,
где
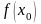 -среднее
значение.
-среднее
значение.