
- •Прямое и обратное преобразование Лапласа. Изображение производных от переменных состояния при нулевых и ненулевых начальных условиях.
- •Прямое и обратное преобразование Фурье. Связь изображений по Лапласу с изображениями по Фурье.
- •Вывод сду, описывающих динамику нагруженного lcr-фвч 2 порядка.
- •Вывод выражений для ачх, фчх и лачх нагруженного lcr-фнч 2 порядка.
- •Вывод выражений для ачх, фчх и лачх нагруженного lcr-фвч 2 порядка.
- •12. Блок-схема алгоритма метода дихотомии для решения нелинейных уравнений.
- •13. Блок-схема алгоритма метода касательных (метода Ньютона) для решения нелинейных уравнений
- •14. Блок-схема алгоритма метода секущих для решения нелинейных уравнений
- •15. Интерполяция функции каноническими полиномами
- •16. Интерполяция функции полиномами Лагранжа
- •17. Интерполяция функции полиномами Ньютона
- •18. Интерполяция функции кубическими сплайнами
- •19. Метод Эйлера для решения дифференциальных уравнений.
- •21. Метод Рунге-Кутта второго порядка с полным шагом для решения дифференциальных уравнений.
- •22. Метод Рунге-Кутта второго порядка с половинным шагом для решения дифференциальных уравнений.
- •23. Метод Рунге-Кутта четвёртого порядка для решения дифференциальных уравнений.
- •24. Дискретное преобразование Фурье.
Прямое и обратное преобразование Лапласа. Изображение производных от переменных состояния при нулевых и ненулевых начальных условиях.
Рис.
4.2.6.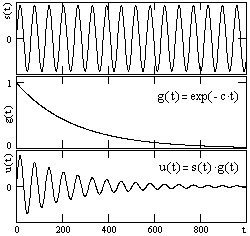
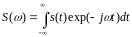 расходится. Умножим s(t) на экспоненциальную
функцию
расходится. Умножим s(t) на экспоненциальную
функцию
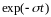 ,
где
,
где
 - положительная константа, и выберем
значение
- положительная константа, и выберем
значение
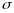 таким, чтобы произведение
таким, чтобы произведение
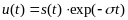 удовлетворяло
условию абсолютной интегрируемости.
Сущность данной операции хорошо видна
на рис. 4.2.6
удовлетворяло
условию абсолютной интегрируемости.
Сущность данной операции хорошо видна
на рис. 4.2.6
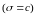 .
Интегрируемость функции u(t) может быть
установлена для любой функции s(t)
соответствующим выбором коэффициента
.
Интегрируемость функции u(t) может быть
установлена для любой функции s(t)
соответствующим выбором коэффициента
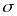 .
При этом спектральная плотность функции
u(t) может быть вычислена по формуле
(4.2.2):
.
При этом спектральная плотность функции
u(t) может быть вычислена по формуле
(4.2.2):
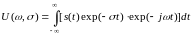 После
объединения экспоненциальных функций
это выражение можно переписать следующим
образом:
После
объединения экспоненциальных функций
это выражение можно переписать следующим
образом:
 (4.2.10)
(4.2.10)
Соответствующее
обратное преобразование Фурье функции
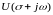 :
:
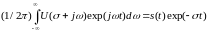 Для
восстановления функции s(t) достаточно
умножить обе части данного выражения
на
Для
восстановления функции s(t) достаточно
умножить обе части данного выражения
на
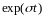 ,
объединить экспоненциальные множители
под интегралом и заменить переменную
интегрирования
,
объединить экспоненциальные множители
под интегралом и заменить переменную
интегрирования
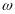 на
на
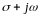 :
:
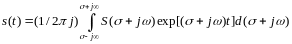
Обозначим
комплексную переменную
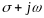 в выражениях (4.2.10,4.2.11) через р (оператор
Лапласа) и получим общепринятую форму
прямого и обратного преобразования
Лапласа:
в выражениях (4.2.10,4.2.11) через р (оператор
Лапласа) и получим общепринятую форму
прямого и обратного преобразования
Лапласа:
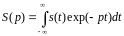 (4.2.10')
(4.2.10')
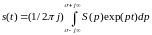
где
 некоторое
вещественное число.
некоторое
вещественное число.
Сигнальную функцию s(t) в преобразованиях Лапласа обычно называют оригиналом, а ее спектральную функцию S(p) - изображением оригинала.
При нулевых начальных условия функции будут иметь вид:
При
 –
площадь сигнала.
–
площадь сигнала.
При

Прямое и обратное преобразование Фурье. Связь изображений по Лапласу с изображениями по Фурье.
Формула прямого преобразования Фурье:
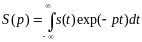
Формула обратного преобразования Фурье:
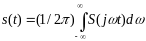
Связь изображений по Лапласу с изображениями по Фурье:
Непрерывное
преобразование Фурье эквивалентно
двустороннему преобразованию Лапласа
с комплексным аргументом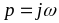 :
:
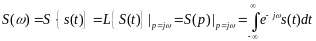
(не уверена в последней формуле, к тому же буквы могу меняться в зависимости от источников)
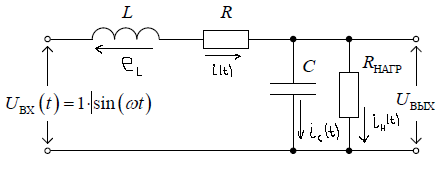
Вывод системы дифференциальных уравнений (СДУ), описывающих динамику нагруженного LCR-ФНЧ 2 порядка.
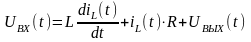
 .
.
Согласно
первому закону Кирхгофа ток катушки
индуктивности
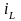 расщепляется на ток конденсатора
расщепляется на ток конденсатора
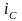 и ток нагрузки
и ток нагрузки
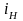 :
:
 .
.
Известно,
что ток конденсатора определяется как
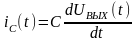 ,
а ток нагрузки по закону Ома выразим
как
,
а ток нагрузки по закону Ома выразим
как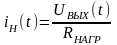 .
.
С учетом данных выражений система дифференциальных уравнений, описывающих состояния ФНЧ, выглядит следующим образом:
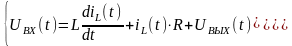 .
.
Применим к полученной системе дифференциальных уравнений прямое преобразование Лапласа, получим систему алгебраических уравнений в изображениях и проведем алгебраические преобразования:
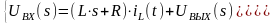 ,
,
где s – оператор Лапласа.
