23. Метод Рунге-Кутта четвёртого порядка для решения дифференциальных уравнений.

Для построения вычислительных схем методов Рунге-Кутты четвертого порядка в тейлоровском разложении искомого решения y(x) учитываются члены, содержащие степени шага h до четвертой включительно. После аппроксимизации производной правой части ОДУ f(x;y) получено семейство схем Рунге-Кутты четвертого порядка, из которых наиболее используемой в вычислительной практике является следующая:

y(x₀+h)=y₀+( k₁ + 2k₂ + 2k₃ + k₄ )/6 + 0(h⁵), (1)

где k₁=hf(x₀,y₀)

k₂= hf(x₀ + h/2, y₀ + k₁/2)

k₃= hf(x₀ + h/2, y₀ + k₂/2)

k₄= hf(x₀ + h, y₀ + k₃)

Схема (1) на каждом шаге h требует вычисления правой части ОДУ в четырех точках. Локальная погрешность схемы имеет пятый порядок, глобальная- четвертый. Схема обобщается для систем ОДУ, записанных в форме Коши. Для удобства програмной реализации, особенно в случае систем ОДУ, формулы (1) рекомендуется преобразовывать к виду

y_i(x₀+h) = y₀ + (q_i1 + 2q_i2 + q_i3 + q_i4)/3 + 0(h⁵), (2)

где q_i1 = h₂f_i (x₀ , y_i0), h₂ = h/2,

q_i2 = h₂f_i (x₀ + h₂ , y_i0 + q_i1),

q_i3 = h₂f_i (x₀ + h₂ , y_i0 + q_i2),

q_i4 = h₂f_i (x₀ + h , y_i0 + q_i3),

i = 1,2,….,n – номер уравнения в системе ОДУ из n уравнений.

24. Дискретное преобразование Фурье.

Дискретное преобразование Фурье— это одно из преобразований Фурье, широко применяемых в алгоритмах цифровой обработки сигналов, а также в других областях, связанных с анализом частот в дискретном (к примеру, оцифрованном аналоговом) сигнале. Дискретное преобразование Фурье требует в качестве входа дискретную функцию. Такие функции часто создаются путём дискретизации (выборки значений из непрерывных функций). Дискретные преобразования Фурье помогают решать частные дифференциальные уравнения и выполнять такие операции, как свёртки. Дискретные преобразования Фурье также активно используются в статистике, при анализе временных рядов.

Прямое преобразование:

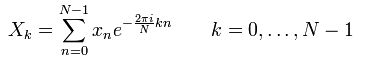
Обратное преобразование:

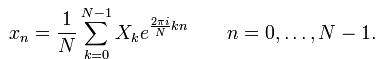
Обозначения:

— N - количество значений сигнала, измеренных за период, а также количество компонент разложения;

—x_n , n=0,….,N-1 - измеренные значения сигнала (в дискретных временных точках с номерами , которые являются входными данными для прямого преобразования и выходными для обратного;

— X _k , k=0,….,N-1, - N комплексных амплитуд синусоидальных сигналов, слагающих исходный сигнал; являются выходными данными для прямого преобразования и входными для обратного; поскольку амплитуды комплексные, то по ним можно вычислить одновременно и амплитуду, и фазу;

— - обычная (вещественная) амплитуда k-го синусоидального сигнала;

— - фаза k-го синусоидального сигнала (аргумент комплексного числа);

— k - индекс частоты. Частота k-го сигнала равна k/T, где T — период времени, в течение которого брались входные данные.

Из последнего видно, что преобразование раскладывает сигнал на синусоидальные составляющие (которые называются гармониками) с частотами от N колебаний за период до одного колебания за период. Поскольку частота дискретизации сама по себе равна N отсчётов за период, то высокочастотные составляющие не могут быть корректно отображены — возникает муаровый эффект. Это приводит к тому, что вторая половина из N комплексных амплитуд, фактически, является зеркальным отображением первой и не несёт дополнительной информации.

Вывод преобразования

Рассмотрим некоторый периодический сигнал x(t) c периодом равным T. Разложим его в ряд Фурье:

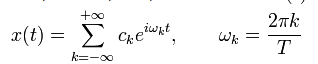
Проведем дискретизацию сигнала так, чтобы на периоде было N отсчетов. Дискретный сигнал представим в виде отсчетов где

, тогда эти отсчеты через ряд Фурье запишутся следующим образом:

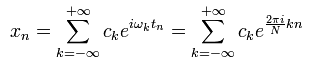
Используя соотношение : 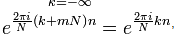получаем :

Таким образом мы получили обратное дискретное преобразование Фурье.

Умножим теперь скалярно выражение для x_n на и получим

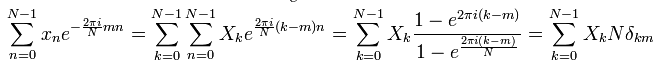
Здесь использованы: а) выражение для суммы конечного числа членов (экспонент) геометрической прогрессии, и б) выражение символа Кронекера как предела отношения функций Эйлера для комплексных чисел. Отсюда следует, что:

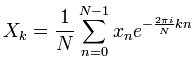
Эта формула описывает прямое дискретное преобразование Фурье.

В литературе принято писать множитель 1/N в обратном преобразовании, и поэтому обычно пишут формулы преобразования в следующем виде:

.
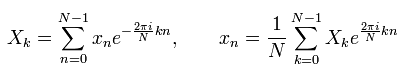