
1.5. Элементарные функции
Понятие элементарной функции
Определение. Функции:
линейная
 (
– постоянная),
(
– постоянная),степеная

показательная
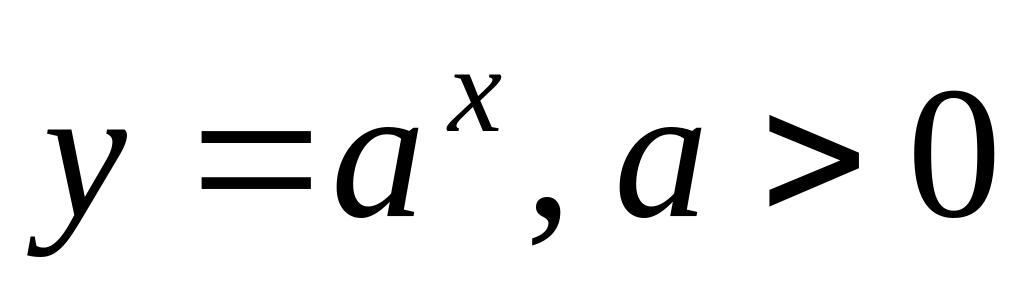 ,
,логарифмическая
 ,
,тригонометрические
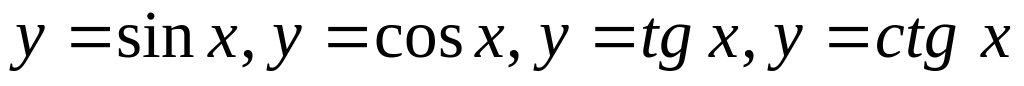 ,
,обратные тригонометрические
 ,
,
называются основными элементарными функциями.
Всякая функция, которая может быть задана с помощью конечного числа арифметических операций (сложение, умножений, вычитание, деление) и конечного числа композиций над основными элементарными функциями, называется элементарной функцией.
В множестве элементарных функций обычно выделяют следующие важные классы .
Многочлены (полиномы) – функции вида
![]() .
.
Здесь
![]() – постоянные (в общем случае, комплексные)
числа, называемые коэффициентами
многочлена,
– натуральное число. Если
– постоянные (в общем случае, комплексные)
числа, называемые коэффициентами
многочлена,
– натуральное число. Если
![]() ,
то
называется степенью
многочлена.
,
то
называется степенью
многочлена.
Многочлены действительного переменного определены на всей числовой прямой.
Алгебраические рациональные функции – функции , представимые в виде
![]() ,
,
где
![]() – многочлены, многочлен
– многочлены, многочлен
![]() не равен тождественно нулю. Рациональные
функции определены всюду, кроме тех
точек, в которых многочлен, стоящий в
знаменателе, равен нулю.
не равен тождественно нулю. Рациональные
функции определены всюду, кроме тех
точек, в которых многочлен, стоящий в
знаменателе, равен нулю.
3. Алгебраические иррациональные функции – функции, не являющиеся рациональными и представимые в виде композиции конечного числа рациональных функций, степенных функций с рациональными показателями и четырех арифметических действий.
Функция
![]()
является иррациональной, поскольку представима в виде композиции степенной функции
![]()
с показателем ½ и многочлена
![]() .
.
4. Трансцендентные функции – элементарные функции, не являющиеся алгебраическими.
К трансцендентным функциям относят, например, функции
![]() .
.
Многочлены. Разложение многочленов на множители
1. Рассмотрим многочлен
![]()
-ой степени. Здесь – комплексное переменное, т.е. переменое, которому придаются значения из множества комлексных чисел , коэффициенты – комплексные числа.
Основная
теорема алгебры многочленов утверждает,
что многочлен
![]() имеет ровно
корней с учетом их кратности:
имеет ровно
корней с учетом их кратности:
![]() ,
,
![]() – комплексные
корни многочлена кратности
– комплексные
корни многочлена кратности
![]() соответственно,
соответственно,
![]() .
.
2. Если многочлен рассматривается над множеством действительных чисел:
![]() ,
,
– действительное
переменное,
- действительные коэффициенты, и
комплексное число
![]() является корнем, то число
является корнем, то число
![]() ,
сопряженное этому числу, также будет
являться корнем многочлена.
,
сопряженное этому числу, также будет
являться корнем многочлена.
В этом случае разложение многочлена на множители над множеством действительных чисел принимает вид:
![]() .
.
Здесь
![]() – действительные
корни многочлена кратности
– действительные
корни многочлена кратности
![]() соответственно, многочлены вторых
степеней имеют комплексно сопряженные
корни кратности
соответственно, многочлены вторых
степеней имеют комплексно сопряженные
корни кратности
![]() соответственно, сумма кратностей корней
соответственно, сумма кратностей корней
![]() .
.
Многочлен
![]() раскладывается на множители:
раскладывается на множители:
![]() .
.
Разложение
свидетельствует о том, что многочлен
имеет пару простых комплексно сопряженных
корней
![]() и действительный корень
и действительный корень
![]() кратности 2.
кратности 2.
Многочлен
![]() раскладывается на множители:
раскладывается на множители:
![]() .
.
Он имеет
действительные корни
![]() ,
причем оба корня кратности 2.
,
причем оба корня кратности 2.
Представление рациональных функций
Рассмотрим функции вида
![]() ,
,
где
![]() –
многочлены степени
и
–
многочлены степени
и
![]() соответственно.
соответственно.
Если
степень числителя строго меньше степени
знаменателя, т.е.
![]() ,
,
то
функция
называется правильной
рациональной дробью,
в противном случае, когда степень
числителя не меньше степени знаменателя,
т.е.
![]() ,
функция называется неправильной
рациональной дробью.
,
функция называется неправильной
рациональной дробью.
Функция
![]() есть пример правильной рациональной
дроби.
есть пример правильной рациональной
дроби.
Функция
![]() дает пример неправильной рациональной
дроби.
дает пример неправильной рациональной
дроби.
Неправильная дробь раскладывается делением числителя на знаменатель в сумму:
![]() .
.
Здесь
![]() – многочлен (n–m)-ой
степени, называемый целой часть
неправильной дроби
,
второе слагаемое
– многочлен (n–m)-ой
степени, называемый целой часть
неправильной дроби
,
второе слагаемое
![]() есть отношение многочленов k-ой
и m-ой
степеней, где k<m,
и называется правильной частью дроби
.
есть отношение многочленов k-ой
и m-ой
степеней, где k<m,
и называется правильной частью дроби
.
Введем в рассмотрение так называемые элементарные дроби. К таковым относят дроби вида
 ,
где
,
где
 – действительные числа,
– действительные числа,
 –
натуральное число;
–
натуральное число;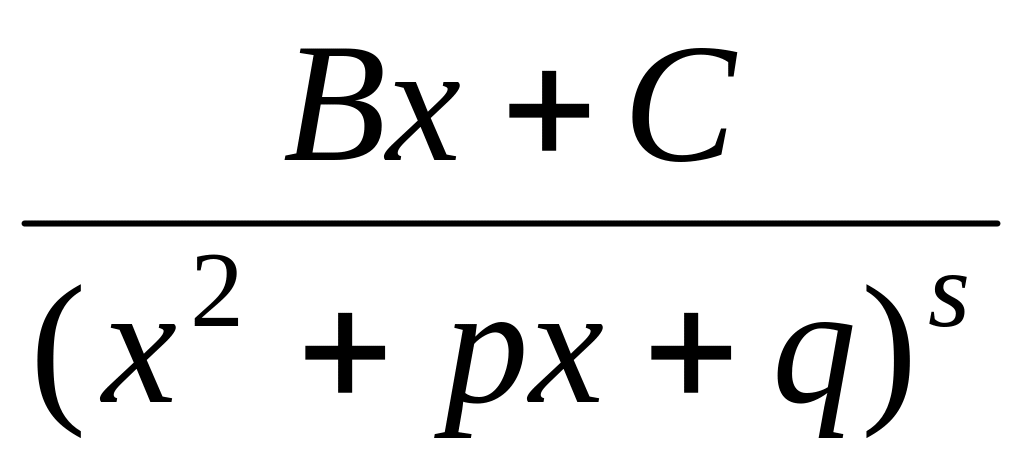 ,
где
,
где
 - действительные числа,
- действительные числа,
 - натуральное число; многочлен 2-ой
степени, стоящий в знаменателе, не имеет
действительных корней.
- натуральное число; многочлен 2-ой
степени, стоящий в знаменателе, не имеет
действительных корней.
Дроби вида 1 будем называть элементарными дробями первого типа, дроби
вида 2 – элементарными дробями иторого типа.
Теорема. Правильная рациональная дробь
с действительными коэффициентами раскладывается в сумму элементарных дробей. При этом, если
![]() ,
,
где
- попарно различные действительные корни многочлена кратности соответственно,
многочлены второй степени не имеют действительных корней, т.е. для любого
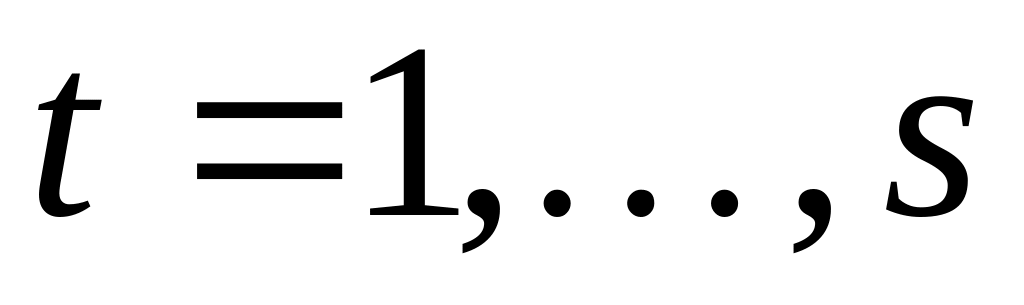
![]() ,
,
![]() - пара
комплексно сопряженных корней многочлена
- пара
комплексно сопряженных корней многочлена
![]() ,
,
 ,
,
то справедливо разложение


![]()

 .
.
Здесь
![]() - некоторые однозначно определяемые
константы.
- некоторые однозначно определяемые
константы.
Теорема утверждает, что разложение правильной рациональной дроби определяется корнями знаменателя, причем
действительному корню
 кратности
кратности
 ,
,
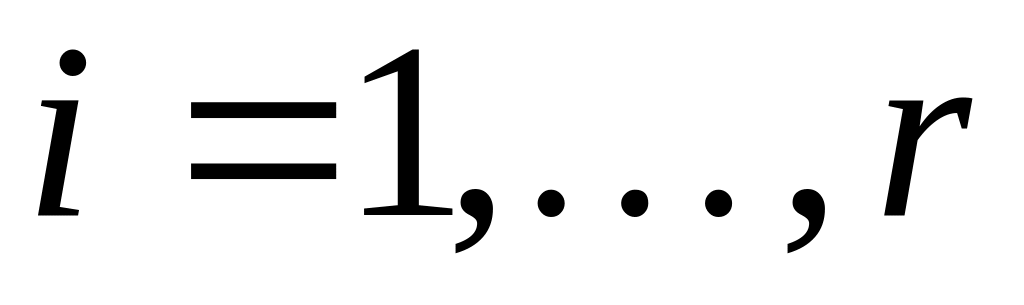 отвечает серия из
элементарных дробей первого типа
отвечает серия из
элементарных дробей первого типа

паре комплексно сопряженных корней
 ,
кратности
,
кратности
 ,
,
отвечает
серия из
элементарных дробей второго типа
,
,
отвечает
серия из
элементарных дробей второго типа
 .
.
Умение раскладывать правильные дроби на сумму элементарных дробей востребуется, в частности, при интегрировании функций.
