
Обратная функция
Пусть
:
X
Y
и для любого y
из Yf
найдется единственный x
из X,
такой, что
=
![]() .
Тогда существует обратная функция
.
Тогда существует обратная функция
–1:
Yf
![]() X.
X.
X
Y
x
y
![]()




![]()
Пример.
Рассмотрим функцию
![]() на полупрямой X={x:
x
на полупрямой X={x:
x![]() 0}.
Множество значений Yf
= {
:
0}.
Множество значений Yf
= {
:
![]() 0},
т.е. здесьY=X.
Выберем произвольно
0},
т.е. здесьY=X.
Выберем произвольно
![]() .
Ему отвечает единственный
.
Ему отвечает единственный
![]() =
=
![]() ,
такой, что
=
.
Действительно,
,
такой, что
=
.
Действительно,
= ( ) = ( )2 = .
Таким образом, обратная функция здесь
![]() .
.
Сложная функция
Пусть
![]() и
и
![]() .
Тогда сложная функция
.
Тогда сложная функция
![]() ,
определенная на множестве
,
определенная на множестве
![]() ,
ставящая в соответствие каждому
,
ставящая в соответствие каждому
![]() точку
точку
![]() называется композицией
(суперпозицией, сложной функцией)
функций
и
называется композицией
(суперпозицией, сложной функцией)
функций
и
![]() ,
и обозначается
,
и обозначается
![]() .
Таким образом,
.
Таким образом,
![]()
X
Y
Z
x
y
z




![]()
![]()
![]()



1.3. Действительные числа
Множество
действительных чисел будем обозначать
![]() .
Любое его подмножество называется
числовым множеством. На множестве
действительных чисел определены операции
сложения и умножения:
.
Любое его подмножество называется
числовым множеством. На множестве
действительных чисел определены операции
сложения и умножения:
каждой паре действительных чисел
 и
и
 ставится в соответствие действительное
число, называемое суммой и обозначаемое
ставится в соответствие действительное
число, называемое суммой и обозначаемое
 ,
,каждой паре действительных чисел и ставится в соответствие действительное число, называемое произведением и обозначаемое
 .
Символ
.
Символ
 в дальнейшем будет, как правило,
опускаться.
в дальнейшем будет, как правило,
опускаться.
Множество действительных чисел обладает следующими свойствами.
А. Операция сложения.
А1.
![]()
![]()
А2.
![]()
![]()
А3.
Существует такое действительное число,
называемое нулем и обозначаемое
![]() ,
что
,
что
![]() .
.
А4.
Для любого действительного числа
найдется такое действительное число
,
что
![]() .
Число
называют противоположным числом к числу
и обозначают
.
Число
называют противоположным числом к числу
и обозначают
![]() .
Число
.
Число
![]() называют разностью чисел
и
.
При этом пишут
называют разностью чисел
и
.
При этом пишут
![]() .
Тем самым определена операция вычитания.
.
Тем самым определена операция вычитания.
B. Операция умножения.
B1.
![]()
B2.
![]()
B3.
Существует действительное число,
называемое единицей и обозначаемое 1,
что
![]() .
.
B4.
Для любого действительного числа
![]() существует действительное число
,
что
существует действительное число
,
что
![]() .
Число
называется
обратным числом к числу
и обозначается
.
Число
называется
обратным числом к числу
и обозначается
![]() .
Число
.
Число
![]() называют
отношением (частным) чисел
и
.
Тем самым определена операция деления.
называют
отношением (частным) чисел
и
.
Тем самым определена операция деления.
С. Связь операций сложения и умножения.
![]()
D. Упорядоченность.
На множестве действительных чисел определено отношение порядка. Для любых двух действительных чисел имеет место одно из двух соотношений:
либо
![]() (“
меньше
”),
или, что то же самое,
(“
меньше
”),
или, что то же самое,
![]() (“
больше
”),
(“
больше
”),
либо
![]() ,
или, что то же самое,
,
или, что то же самое,
![]() .
.
При этом выполняются следующие условия:
D1.
Если
и
![]() ,
то
,
то
![]() .
.
D2.
Если
,
то
![]() .
.
D3.
Если
и
![]() ,
то
,
то
![]() .
.
Соотношения
порядка называют также сравнением
действительных чисел по величине, или
неравенствами. Запись
![]() означает,
что либо
,
либо
означает,
что либо
,
либо
![]() .
.
Из
свойств D2
- D3
следует
важное свойство множества действительных
чисел, называемое плотностью действительных
чисел: для любых двух различных
действительных чисел
и
,
,найдется
такое третье число
![]() ,
что
,
что
![]() .
.
E. Непрерывность множества действительных чисел.
Для
любых числовых множеств
и
![]() таких, что любая пара чисел
таких, что любая пара чисел
![]() и
и
![]() стеснена
неравенством
стеснена
неравенством
![]() ,
существует такое число
,
существует такое число
![]() ,
что
,
что
![]() .
.
Перечисленные свойства полностью определяют множество действительных чисел
Важные подмножества действительных чисел
1.
Числа 1,2,3,… называются натуральными
числами. Множество натуральных чисел
будем обозначать
![]() .
.
2.
Множество
![]() называется множеством целых чисел.
Очевидно,
называется множеством целых чисел.
Очевидно,![]()
3.
Множество
![]() называется множеством рациональных
чисел. Очевидно,
называется множеством рациональных
чисел. Очевидно,
![]() .
.
4.
Множество
![]() – дополнение множества рациональных
чисел до множества действительных
чисел, называется множеством иррациональных
чисел.
– дополнение множества рациональных
чисел до множества действительных
чисел, называется множеством иррациональных
чисел.
5. Пусть и – два действительных числа, . Выделяют следующие типы числовых множеств, называемые числовыми промежутками:
![]() – отрезок,
– отрезок,
![]() – интервал,
– интервал,
![]()
![]() – полуинтервалы.
– полуинтервалы.
Определение.
Числовое множество
называют
ограниченным сверху, если существует
такое число
![]() ,
что для всех
имеет
место неравенство
,
что для всех
имеет
место неравенство
![]() .
Число
называют в этом случае числом,
ограничивающим сверху множество
.
.
Число
называют в этом случае числом,
ограничивающим сверху множество
.
Пример.
Промежуток
![]() является примером ограниченного сверху
множества. В качестве числа
,
ограничивающего сверху это множество,
может быть выбрано любое неотрицательное
число.
является примером ограниченного сверху
множества. В качестве числа
,
ограничивающего сверху это множество,
может быть выбрано любое неотрицательное
число.
Определение.
Числовое множество
называют
ограниченным снизу, если существует
такое число
![]() ,
что для всех
имеет
место неравенство
,
что для всех
имеет
место неравенство
![]() .
Число
называют в этом случае числом,
ограничивающим снизу множество
.
.
Число
называют в этом случае числом,
ограничивающим снизу множество
.
Пример.
Промежуток
![]() является примером ограниченного снизу
множества. В качестве числа
,
ограничивающего снизу это множество,
может быть выбрано любое неположительное
число.
является примером ограниченного снизу
множества. В качестве числа
,
ограничивающего снизу это множество,
может быть выбрано любое неположительное
число.
Определение. Числовое множество называют ограниченным, если оно ограничено сверху и снизу.
Пример
1. Интервал
![]() является ограниченным множеством,
поскольку он ограничен сверху и снизу.
Действительно, в качестве числа
,
ограничивающего снизу это множество
может быть выбрано, например, число
является ограниченным множеством,
поскольку он ограничен сверху и снизу.
Действительно, в качестве числа
,
ограничивающего снизу это множество
может быть выбрано, например, число
![]() ,
а в качестве числа, ограничивающего
множество сверху, выступает, например,
число
,
а в качестве числа, ограничивающего
множество сверху, выступает, например,
число
![]() .
.
Пример
2. Промежуток
![]() является ограниченным снизу и
неограниченным сверху числовым
множеством. Промежуток
является примером ограниченного сверху,
но неограниченного снизу числового
множества.
является ограниченным снизу и
неограниченным сверху числовым
множеством. Промежуток
является примером ограниченного сверху,
но неограниченного снизу числового
множества.
Определение 1. Если числовое множество ограничено сверху, то наименьшее из чисел, ограничивающих сверху множество , называют его верхней гранью и обозначают
![]() ,
или
,
или
![]()
(от латинского слова supremum – наибольший).
Определение 2. Если числовое множество ограничено снизу, то наибольшее из чисел, ограничивающих снизу множество, называют его нижней гранью и обозначают
![]() ,
или
,
или
![]()
(от латинского слова infinum – наименьший).
Приведенные выше содержательные определения верхней и нижней граней числовых множеств могут быть переформулированы и даны в строгой математической форме.
Определение 1*. Число называется верхней гранью числового множества , если
для любого выполняется неравенство
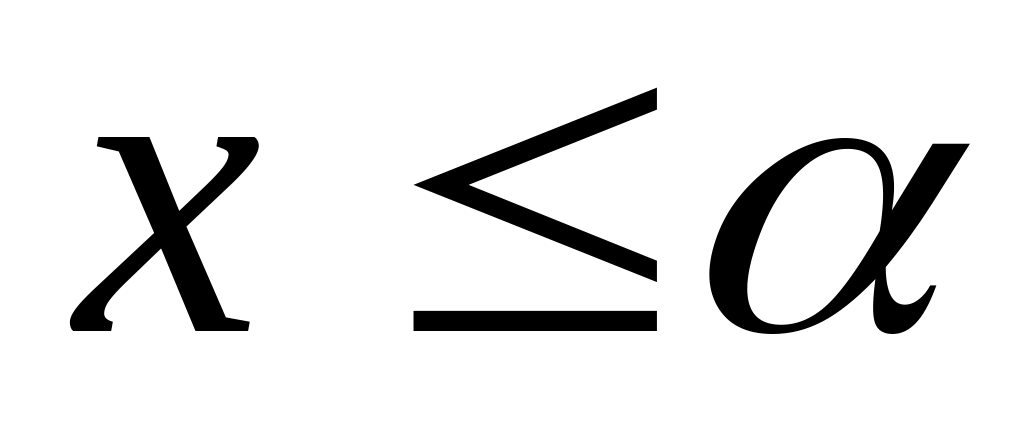 ;
;для любого числа
 существует число
,
что
существует число
,
что
 .
.
Определение 2*. Число называется нижней гранью числового множества , если
для любого выполняется неравенство
 ;
;для любого числа
 существует число
,
что
существует число
,
что
 .
.
Пример
1. Рассмотрим множество
![]() .
Оно является ограниченным.
Не трудно убедиться, что среди всех
чисел, ограничивающих сверху это
множество, наименьшим является число
2, а из всех чисел, ограничивающих
множество снизу, наибольшим является
число –1. Таким образом,
.
Оно является ограниченным.
Не трудно убедиться, что среди всех
чисел, ограничивающих сверху это
множество, наименьшим является число
2, а из всех чисел, ограничивающих
множество снизу, наибольшим является
число –1. Таким образом,
![]() .
.
Заметим,
что если точная грань множества
достигается на этом множестве, т.е
принадлежит рассматриваемому множеству,
то вместо
![]() и
и
![]() пишут
пишут
![]() и
и
![]() соответственно.
соответственно.
Пример
2. Рассмотрим
полуинтервал [0,4). Не трудно видеть, что
![]() ,
причем здесь
,
причем здесь
![]() ,
,
![]() ,
т.е. нижняя грань принадлежит множеству,
а верхняя грань ему не принадлежит. В
этом случае мы вправе написать
,
т.е. нижняя грань принадлежит множеству,
а верхняя грань ему не принадлежит. В
этом случае мы вправе написать
![]() .
.
