
- •Рекомендуемая литература
- •Теория вероятностей
- •1. Случайные события
- •1.1. Событие и эксперимент. Соотношения между событиями. Пространство элементарных событий
- •1.2. Частота события. Статистическое определение вероятности
- •1.3. Классическое определение вероятности
- •1.4. Геометрическое определение вероятности
- •1.5. Аксиомы теории вероятностей. Основные следствия из аксиом
- •1.6. Условная вероятность. Независимость событий. Теорема умножения вероятностей
- •1.7. Теорема сложения вероятностей
- •1.8. Формула полной вероятности. Формула Байеса
- •1.9. Вычисление вероятностей событий с помощью биномиальной и полиномиальной формул
- •2. Случайные величины
- •2.1. Понятие случайной величины и её закона распределения. Дискретные и непрерывные величины
- •2.2. Ряд и многоугольник распределения дискретной св
- •2.3. Функция распределения св и её свойства
- •2.4. Плотность распределения непрерывной св и её свойства
- •2.5. Математическое ожидание, мода и квантили св
- •2.6. Моменты, дисперсия и среднее квадратическое отклонение св
- •2.7. Биномиальное распределение
- •2.8. Распределение Пуассона
- •2.9. Геометрическое распределение
- •2.10. Равномерное распределение
- •2.11. Показательное распределение
- •2.12. Одномерное нормальное распределение
2.7. Биномиальное распределение
Дискретная СВ Х с возможными
значениями
![]() называется распределённой по биномиальному
закону, если её ряд распределения
задаётся формулой
называется распределённой по биномиальному
закону, если её ряд распределения
задаётся формулой
![]() ,
,
![]() ,
,
где
![]() и
и
![]() – параметры биномиального распределения
и
.
Для биномиального закона
– параметры биномиального распределения
и
.
Для биномиального закона
![]() ,
,
![]() .
.
Данное распределение возникает в схеме Бернулли, где р – вероятность появления события А в одном испытании, Х – число появлений события А в n независимых испытаниях.
2.8. Распределение Пуассона
Дискретная СВ Х с возможными
значениями
![]() называется распределённой по закону
Пуассона с параметром
называется распределённой по закону
Пуассона с параметром
![]() ,
если её ряд распределения задаётся
формулой
,
если её ряд распределения задаётся
формулой
![]() ,
,
![]()
Для закона Пуассона
![]() .
.
Доказано, что биномиальное распределение
при одновременном увеличении n
и уменьшении р с сохранением
постоянного значения
![]() неограниченно приближается к распределению
Пуассона с параметром
неограниченно приближается к распределению
Пуассона с параметром
![]() .
Это означает, что при большом n и
малом р вероятность
.
Это означает, что при большом n и
малом р вероятность
![]() ,
где Х – число появлений события А
в n независимых испытаниях, может
быть приближённо вычислена по формуле
распределения Пуассона.
,
где Х – число появлений события А
в n независимых испытаниях, может
быть приближённо вычислена по формуле
распределения Пуассона.
2.9. Геометрическое распределение
Дискретная СВ Х с возможными
значениями
![]() называется распределённой по
геометрическому закону, если её ряд
распределения задаётся формулой
называется распределённой по
геометрическому закону, если её ряд
распределения задаётся формулой
![]() ,
,
![]() ,
,
где
– параметр геометрического распределения
и
.
Для геометрического закона
![]() ,
,
![]() .
.
Данное распределение возникает при повторных независимых испытаниях, где р – вероятность появления события А в одном испытании, Х – число испытаний, проведённых до первого появления события А.
2.10. Равномерное распределение
Непрерывная СВ Х называется равномерно
распределённой на отрезке
![]() ,
если множество её возможных значений
– отрезок
,
а вероятность попадания СВ Х на
любой участок этого отрезка пропорциональна
длине участка. Плотность и функция
распределения равномерно распределённой
СВ имеют вид:
,
если множество её возможных значений
– отрезок
,
а вероятность попадания СВ Х на
любой участок этого отрезка пропорциональна
длине участка. Плотность и функция
распределения равномерно распределённой
СВ имеют вид:
![]()
![]()
Для равномерного распределения
![]() ,
,
![]() .
.
2.11. Показательное распределение
Непрерывная СВ Х называется
распределённой по показательному
(экспоненциальному) закону c
параметром
,
если множество её возможных значений
– полупрямая
![]() ,
а плотность и функция распределения
имеют вид:
,
а плотность и функция распределения
имеют вид:
![]()
![]()
Для показательного распределения
![]() ,
,
![]() .
.
2.12. Одномерное нормальное распределение
Непрерывная СВ Х называется
распределённой по нормальному закону
(по закону Гаусса) с параметрами
![]() и
и
![]() ,
если множество её возможных значений
– вся числовая прямая, а плотность
вероятности определяется формулой
,
если множество её возможных значений
– вся числовая прямая, а плотность
вероятности определяется формулой
 .
.
Для нормального закона используется
обозначение
![]() ,
при этом
,
при этом
![]() ,
,
![]() ,
а функция распределения задаётся
формулой
,
а функция распределения задаётся
формулой
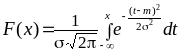 ,
,
где интеграл не выражается через элементарные функции. Графики плотности и функции распределения имеют вид:
Нормальный закон распределения называется
стандартным, если
![]() и
и
![]() .
Для стандартного нормального закона
плотность вероятности имеет вид
.
Для стандартного нормального закона
плотность вероятности имеет вид
![]() и обладает свойством
и обладает свойством
![]() ,
а функция распределения имеет вид
,
а функция распределения имеет вид
![]() и обладает свойством
и обладает свойством
![]() .
Функции
.
Функции
![]() и
и
![]() называются, соответственно, функцией
Гаусса и функцией Лапласа. Для нахождения
их значений при различных х составлены
таблицы.
называются, соответственно, функцией
Гаусса и функцией Лапласа. Для нахождения
их значений при различных х составлены
таблицы.
Если в выражении для функции распределения
СВ
сделать замену
![]() ,
то получим
,
то получим
![]() .
При
.
При
![]() имеем
имеем
![]() ,
а при
,
а при
![]() имеем
имеем
![]() .
Отсюда
.
Отсюда
![]() ,
,
т.е. функция распределения нормального закона с заданными параметрами m и выражается через функцию распределения стандартного нормального закона.
Поскольку для непрерывной СВ
![]() ,
то для нормально распределённой СВ
,
то для нормально распределённой СВ
![]() .
В частности,
.
В частности,
![]() .
.
Это означает, что попадание нормально
распределённой СВ Х на отрезок
![]() – практически достоверное событие.
Данное свойство нормального распределения
называется “правилом трёх сигма”.
– практически достоверное событие.
Данное свойство нормального распределения
называется “правилом трёх сигма”.
