
- •Матрицы, определители, системы лин. Уравнений
- •1.Матрицы и операции над ними: сложение, умножение на скаляр, произведение матриц. Свойства этих операций.
- •2.Определители произвольного порядка и их свойства. Теорема о разложении определителя по элементам строки (столбца) и следствия из нее. Необходимое и достаточное условие обращения в ноль определителя.
- •Следствие 2 (фальшивое разложение определителя)
- •3.Произвольные системы линейных уравнений. Метод Гаусса. Квадратные системы с невырожденным определителем. Формулы Крамера.
- •Векторная алгебра
- •4. Векторы. Простейшие операции над ними и их свойства. Линейная комбинация и линейная зависимость системы векторов.
- •Скалярное произведение двух векторов, его свойства и вычисление его в координатах. Применение скалярного произведения в геометрии и механике.
- •Аналитическая геометрия
- •Аффинная и декартова система координат на плоскости и в пространстве.
- •Уравнения фигуры. Основные теоремы об уравнениях и о фигурах, определяемых ими. Порядок алгебраической фигуры.
Скалярное произведение двух векторов, его свойства и вычисление его в координатах. Применение скалярного произведения в геометрии и механике.
Скаля́рное произведе́ние — операция над двумя векторами, результатом которой является число (скаляр), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение длины данного вектора x на проекцию другого вектора y на данный вектор x. Скалярное произведение обладает переместительным свойством: ab=ba
 Векторы
Векторы ![]() и
и ![]() заданы
своими координатами:
заданы
своими координатами:![]() ,
, ![]() ,то
их скалярное произведение может быть
вычислено по формуле
,то
их скалярное произведение может быть
вычислено по формуле![]() .
.
Отсюда следует необходимое и достаточное
условие перпендикулярности двух
векторов![]() .Угол
.Угол ![]() между
векторами
,
,дается
формулой
между
векторами
,
,дается
формулой 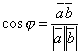 ,
или в координатах
,
или в координатах![]() .
.
|
Любые геометрические вычисления (как собственно в математике, так и в приложениях), связанные с длинами, углами, проецированием, ортогональностью. В механике, наиболее характерным применением скалярного произведения является вычисление работы.
Правые и левые базисы на плоскости и в пространстве. Векторное произведение двух векторов и смешанное произведение трех векторов в ориентированном пространстве, их свойства. Вычисление в ортонормированном базисе векторного произведения двух векторов и смешанного произведения трех векторов. Их применения.
В пространстве различают правые и левые
тройки векторов. Тройка некомпланарных
векторов ![]() наз.
правой, если наблюдателю из их общего
начала обход концов векторов
наз.
правой, если наблюдателю из их общего
начала обход концов векторов ![]() в
указанном порядке кажется совершающимся
по часовой стрелке. В противном случае
в
указанном порядке кажется совершающимся
по часовой стрелке. В противном случае ![]() -
левая тройка. Правая (левая) тройка
векторов располагается так, как могут
быть расположены соответственно большой,
несогнутый указательный и средний
пальцы правой (левой) руки .Все правые
(или левые) тройки векторов наз. одинаково
ориентированными. Ниже тройка векторов
базиса
-
левая тройка. Правая (левая) тройка
векторов располагается так, как могут
быть расположены соответственно большой,
несогнутый указательный и средний
пальцы правой (левой) руки .Все правые
(или левые) тройки векторов наз. одинаково
ориентированными. Ниже тройка векторов
базиса ![]() считается
правой.
считается
правой.
Векторным произведением вектора а на вектор b называется вектор, который:
1. Перпендикулярен векторам a и b,
т. е. с^а и с^b; 2. Имеет длину,
численно равную площади параллелограмма,
построенного на векторах а и b как
на сторонах, т. е. ![]() 3.Векторы a, b и с образуют
правую тройку.
3.Векторы a, b и с образуют
правую тройку.
Свойства векторного произведения
1. При перестановке сомножителей векторное произведение меняет знак, т.е. а хb =(b хa ) Векторы ахb и b ха коллинеарны, имеют одинаковые модули (площадь параллелограмма остается неизменной), но противоположно направлены (тройки а , b , а хb и a , b , bxa противоположной ориентации). Стало быть axb = -(bxa ).
2. Векторное произведение обладает
сочетательным свойством относительно
скалярного множителя, т. е. l(а хb )
= (lа ) х b = а х (lb ). Модуль
векторного произведения ![]() равняется
площади
равняется
площади ![]() параллелограмма,
построенного на приведённых к общему
началу векторах
параллелограмма,
построенного на приведённых к общему
началу векторах ![]() и
и
Если ![]() — единичный
вектор, ортогональный векторам
и
— единичный
вектор, ортогональный векторам
и ![]() и
выбранный так, что тройка
и
выбранный так, что тройка ![]() —
правая, а
—
площадь параллелограмма, построенного
на них (приведённых к общему началу), то
для векторного произведения справедлива
формула:
—
правая, а
—
площадь параллелограмма, построенного
на них (приведённых к общему началу), то
для векторного произведения справедлива
формула:
![]()
Если ![]() —
какой-нибудь вектор,
—
какой-нибудь вектор, ![]() —
любая плоскость, содержащая этот
вектор,
—
единичный вектор, лежащий в плоскости
и
ортогональный к
,
—
любая плоскость, содержащая этот
вектор,
—
единичный вектор, лежащий в плоскости
и
ортогональный к
, ![]() —
единичный вектор, ортогональный к
плоскости
и
направленный так, что тройка
векторов
—
единичный вектор, ортогональный к
плоскости
и
направленный так, что тройка
векторов ![]() является
правой, то для любого лежащего в
плоскости
вектора
справедлива
формула
является
правой, то для любого лежащего в
плоскости
вектора
справедлива
формула
![]()
При использовании векторного и скалярного произведений можно высчитать объём параллелепипеда, построенного на приведённых к общему началу векторах a, b и c (см. Рисунок 2). Такое произведение трех векторов называется смешанным.
![]()
Сме́шанное произведе́ние ![]() векторов
векторов ![]() — скалярное
произведение вектора
(
умножение длины данного вектора
x на проекцию другого вектора y на
данный вектор x) на векторное
произведениевекторов
и
:
— скалярное
произведение вектора
(
умножение длины данного вектора
x на проекцию другого вектора y на
данный вектор x) на векторное
произведениевекторов
и
:
![]() .
.
Иногда его называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр).Смешанное произведение кососимметрично по отношению ко всем своим аргументам:
![]()
т. е. перестановка любых двух сомножителей меняет знак произведения. Отсюда следует, что
![]() Смешанное
произведение
в
правой декартовой системе координат
(в ортонормированном базисе)
равноопределителю матрицы,
составленной из векторов
Смешанное
произведение
в
правой декартовой системе координат
(в ортонормированном базисе)
равноопределителю матрицы,
составленной из векторов ![]() и
:
и
:
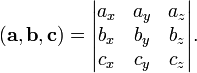 Смешанное
произведение
в
левой декартовой системе координат (в
ортонормированном базисе)
равноопределителю матрицы,
составленной из векторов
и
,
взятому со знаком "минус":
Смешанное
произведение
в
левой декартовой системе координат (в
ортонормированном базисе)
равноопределителю матрицы,
составленной из векторов
и
,
взятому со знаком "минус":
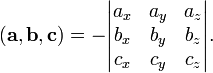
В частности Если любые два вектора параллельны, то с любым третьим вектором они образуют смешанное произведение равное нулю. Если три вектора линейно зависимы (т. е. компланарны, лежат в одной плоскости), то их смешанное произведение равно нулю. Геометрический смысл — Смешанное произведение по абсолютному значению равно объёму параллелепипеда(см. рисунок), образованного векторами и ; знак зависит от того, является ли эта тройка векторов правой или левой.
Тройно́е ве́кторное произведе́ние (другое
название: двойное векторное
произведение) ![]() векторов
векторов ![]() —векторное
произведение вектора
—векторное
произведение вектора ![]() на
векторное произведение векторов
на
векторное произведение векторов ![]() и
и ![]()
![]()
Базис называется ортонормированным, если его векторы попарно ортогональны и равны единице.
