1. Матрицы, определители, системы лин. Уравнений

1.Матрицы и операции над ними: сложение, умножение на скаляр, произведение матриц. Свойства этих операций.

Матрицей размера mn, где m-число строк, n-число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются aij, где i- номер строки, а j- номер столбца.А = 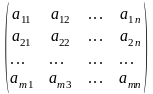Матрица может состоять как из одной строки, так и из одного столбца. Вообще говоря, матрица может состоять даже из одного элемента.

Определение. Если число столбцов матрицы равно числу строк (m=n), то матрица называется квадратной.

Определение. Матрица вида: = E, называется единичной матрицей.

Определение. Если amn = anm , то матрица называется симметрической.

Пример: 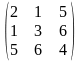- симметрическая матрица

Основные действия над матрицами

Сумма (разность) матриц.

Сложение и вычитание матриц сводится к соответствующим операциям над их элементами. Самым главным свойством этих операций является то, что они определены только для матриц одинакового размера.

Суммой (разностью) матриц является матрица, элементами которой являются соответственно сумма (разность) элементов исходных матриц.

cij = aij  bij

Обозначение: С = А + В = В + А.

Умножение матрицы на число.

Операция умножения матрицы любого размера на произвольное число сводится к умножению каждого элемента матрицы на это число. 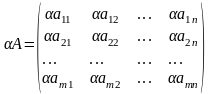Свойства: (АВ) =А  В

А() = А  А

Произведение двух матриц.

Замечание: Операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй. В противном случае произведение матриц не определено.

Произведением матриц называется матрица, элементы которой могут быть вычислены по следующим формулам: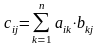 Обозначение: AB = C;Из приведенного определения видно, что каждый элемент матрицы С равен алгебраической сумме произведений элементов i – той строки матрицы А на соответствующие элементы j – го столбца матрицы В.Отсюда правило: строка*столбец

Свойства:

1) Умножение матриц не коммутативно, т.е. АВ  ВА даже если определены оба произведения. Однако, если для каких – либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными. Самым характерным примером может служить единичная матрица, которая является перестановочной с любой другой матрицей того же размера.

2) Операция перемножения матриц ассоциативна, т.е. если определены произведения АВ и (АВ)С, то определены ВС и А(ВС), и выполняется равенство:

(АВ)С=А(ВС).

3) Операция умножения матриц дистрибутивна по отношению к сложению, т.е. если имеют смысл выражения А(В+С) и (А+В)С, то соответственно:

А(В + С) = АВ + АС

(А + В)С = АС + ВС.

4) Если произведение АВ определено, то для любого числа  верно соотношение:

(AB) = (A)B = A(B).

2.Определители произвольного порядка и их свойства. Теорема о разложении определителя по элементам строки (столбца) и следствия из нее. Необходимое и достаточное условие обращения в ноль определителя.

Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно).

свойства определителей относительно преобразования матриц:

1. Определитель не меняется при транспонировании. Это означает, что определитель матрицы равен определителю транспонированной матрицы (матрицы, в которой строки заменены соответствующими столбцами).

Исходя из первого свойства, в остальных свойствах мы можем говорить только о строках, подразумевая, что эти свойства применими также и к столбцам.

2. Если одна из строк определителя состоит из нулей, то определитель равен нулю.

3. От перестановки двух строк определитель меняет свой знак.

4. Определитель, содержащий две одинаковые строки, равен нулю.

5. Если все элементы некоторой строки умножить на некое число, то сам определитель умножится на это число.

6. Определитель, содержащий две пропорциональные строки, равен нулю.

7. Если все элементы i-й строки определителя n-го порядка представлен в виде суммы двух слагаемых: aij=bj+cj, j = 1, ..., n, то определитель равен сумме двух определителей, у которых все строки, кроме i-й, - такие же, как и в заданом определителе, а i-я строка в одном из слагаемых состоит из элементов bj, в другом - из элементов cj.

8. Если одна из строк определителя есть линейная комбинация его других строк, то определитеь равен нулю..

9. Определитель не меняется, если к одной из его строк прибавляется любая линейная комбинация других строк.

Теорема (о разложении определителя по строке): определитель равен сумме произведений всех элементов какой-либо строки на их алгебраические дополнения. Это означает, что определитель матрицы n×n равен   .где   — алгебраическое дополнение к минору, расположенному в строке с номером   и столбце с номером  .   также называют алгебраическим дополнением к элементу  .

Утверждение является частным случаем теоремы Лапласа. Достаточно в ней положить   равным 1 и выбрать  -ую строку, тогда минорами, расположенными в этой строке будут сами элементы.

Теорема Лапласа

Пусть выбраны любые   строк матрицы  . Тогда определитель матрицы   равен сумме всевозможных произведений миноров  -го порядка, расположенных в этих строках, на их алгебраические дополнения. где суммирование ведётся по всевозможным номерам столбцов