
- •Матрицы, определители, системы лин. Уравнений
- •1.Матрицы и операции над ними: сложение, умножение на скаляр, произведение матриц. Свойства этих операций.
- •2.Определители произвольного порядка и их свойства. Теорема о разложении определителя по элементам строки (столбца) и следствия из нее. Необходимое и достаточное условие обращения в ноль определителя.
- •Следствие 2 (фальшивое разложение определителя)
- •3.Произвольные системы линейных уравнений. Метод Гаусса. Квадратные системы с невырожденным определителем. Формулы Крамера.
- •Векторная алгебра
- •4. Векторы. Простейшие операции над ними и их свойства. Линейная комбинация и линейная зависимость системы векторов.
- •Скалярное произведение двух векторов, его свойства и вычисление его в координатах. Применение скалярного произведения в геометрии и механике.
- •Аналитическая геометрия
- •Аффинная и декартова система координат на плоскости и в пространстве.
- •Уравнения фигуры. Основные теоремы об уравнениях и о фигурах, определяемых ими. Порядок алгебраической фигуры.
Следствие 2 (фальшивое разложение определителя)
Сумма произведений всех элементов некоторой строки (столбца) матрицы А на алгебраические дополнения соответствующих элементов любой другой строки (столбца) равна нулю.
Доказательство. Рассмотрим сумму произведений всех элементов произвольной k-ой строки матрицы А на алгебраические дополнения соответствующих элементов любой другой, скажем, i-ой строки матрицы А. Пусть A′ – матрица, у которой все строки, кроме i-ой, такие же, как у матрицы А, а элементами i-ой строки матрицы A′ являются соответствующие элементы k-ой строки матрицы А. Тогда у матрицы A′ две одинаковые строки и, следовательно, по свойству матрицы об одинаковых строках имеем, что |A′| = 0 . С другой стороны, по следствию 1 определитель |A′| равен сумме произведений всех элементов i-ой строки матрицы A′ на их алгебраические дополнения. Заметим, что алгебраические дополнения элементов i-ой строки матрицы A′ совпадают с алгебраическими дополнениями соответствующих элементов i-ой строки матрицы А. Но элементами i-ой строки матрицы A′ являются соответствующие элементы k-ой строки матри- цы А. Таким образом, сумма произведений всех элементов i-ой строки матрицы A′ на их алгебраические дополнения с одной стороны равна нулю, а с другой стороны равна сумме произведений всех элементов k-ой строки матрицы А на алгебраические дополнения соответствующих элементов i-ой строки матрицы А.
Необходимое и достаточное условие равенства нулю определителя.
Теорема: Определитель квадратной матрицы равен нулю тогда и только тогда, когда его столбцы/строки линейно зависимы.
3.Произвольные системы линейных уравнений. Метод Гаусса. Квадратные системы с невырожденным определителем. Формулы Крамера.
Произвольные системы
линейных алгебраических уравнений.

или в матричной форме,
АХ = b, где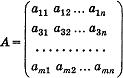 -
матрица системы, размера m x n,
-
матрица системы, размера m x n,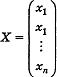 -
матрица-столбец неизвестных,
-
матрица-столбец неизвестных,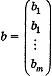 -
матрица-столбец свободных членов данной
системы.
Решением системы называется
такая совокупность n чисел
-
матрица-столбец свободных членов данной
системы.
Решением системы называется
такая совокупность n чисел ![]() ,
, ![]() ,...,
,..., ![]() ,
что при подстановке их во все уравнения
системы вместо соответствующих
неизвестных получаются числовые
тождества.
Формулы
Крамера имеют вид:
,
что при подстановке их во все уравнения
системы вместо соответствующих
неизвестных получаются числовые
тождества.
Формулы
Крамера имеют вид:

Если количество строк матрицы равно количеству столбцов, то такая матрица называется квадратной. Квадратная матрица невырожденная - то есть её определитель не равен нулю.
Ме́тод Га́усса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Минор матрицы
― определитель такой
квадратной матрицы ![]() порядка
(который
называется также порядком этого минора),
элементы которой стоят в матрице
на
пересечении строк с номерами
порядка
(который
называется также порядком этого минора),
элементы которой стоят в матрице
на
пересечении строк с номерами ![]() и
столбцов с номерами
и
столбцов с номерами ![]() .
.
Базисным минором матрицы называется любой её ненулевой минор максимального порядка. Для того чтобы минор был базисным, необходимо и достаточно, чтобы все окаймляющие его миноры (то есть содержащие его миноры на единицу большего порядка) были равны нулю. Система строк (столбцов) матрицы, связанных с базисным минором, является максимальной линейно независимой подсистемой системы всех строк (столбцов) матрицы.
Рангом системы
строк (столбцов) матрицы
с ![]() строк
и
строк
и ![]() столбцов
называется максимальное число линейно
независимыхстрок (столбцов). Несколько
строк (столбцов) называются линейно
независимыми, если ни одна из них не
выражается линейно через другие. Ранг
системы строк всегда равен рангу системы
столбцов, и это число называется рангом
матрицы.
столбцов
называется максимальное число линейно
независимыхстрок (столбцов). Несколько
строк (столбцов) называются линейно
независимыми, если ни одна из них не
выражается линейно через другие. Ранг
системы строк всегда равен рангу системы
столбцов, и это число называется рангом
матрицы.
Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.
Ранг матрицы —
Размерность образа ![]() линейного
оператора, которому соответствует
матрица.
линейного
оператора, которому соответствует
матрица.
