Тема 3. Метод разделения переменных для решения краевых задач.
Найти формы и частоты свободных продольных гармонических колебаний стержня, левый конец которого (х = 1/2) свободен от нагрузки, а правый (x = 3/2) жестко закреплен.
Собственные частоты
колебаний
определяются через собственные значения
по
формуле
,
где
,
–модуль
упругости и плотность материала стержня.
Решение.
Запишем условие задачи:
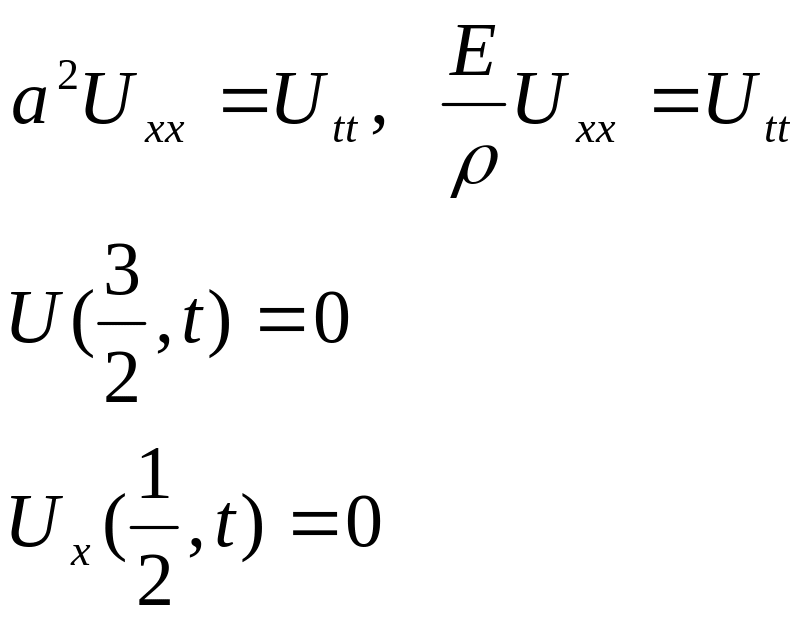Даны
краевые условия 3 типа.
Решим данную задачу методом Фурье.
Решение данной задачи представиться в
виде:
.
Проведем разделение переменных:
.
-
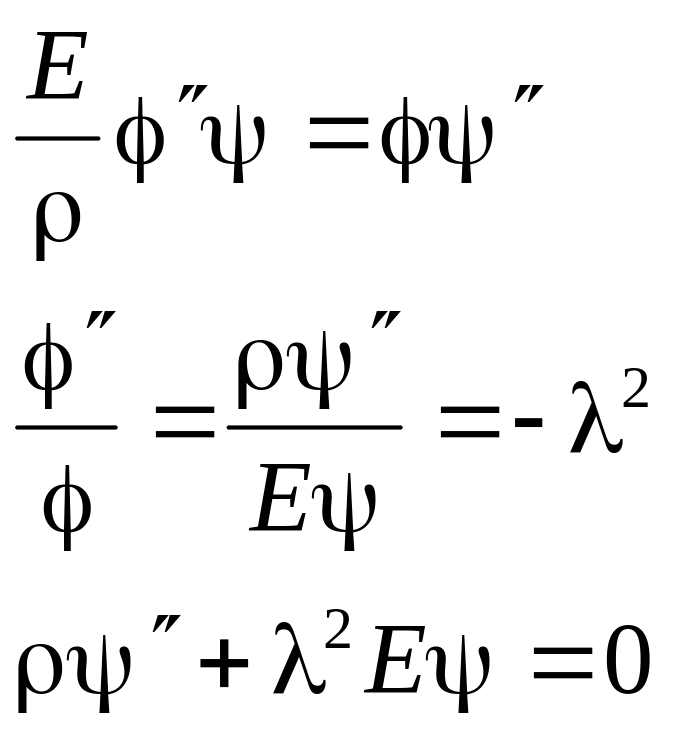
Задача Штурма-Лиувилля.
Решение:
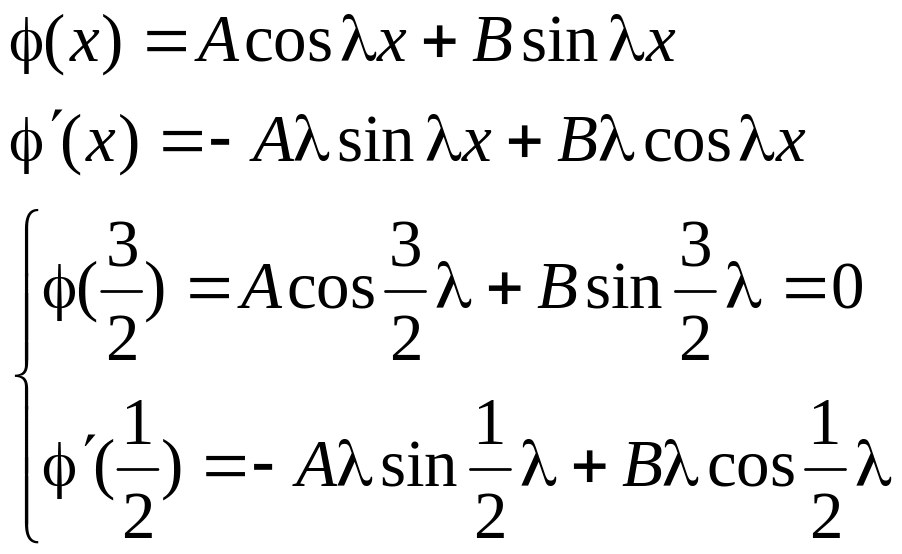
Чтобы система имела нетривиальные решения определитель должен быть равен 0:
,=>
-
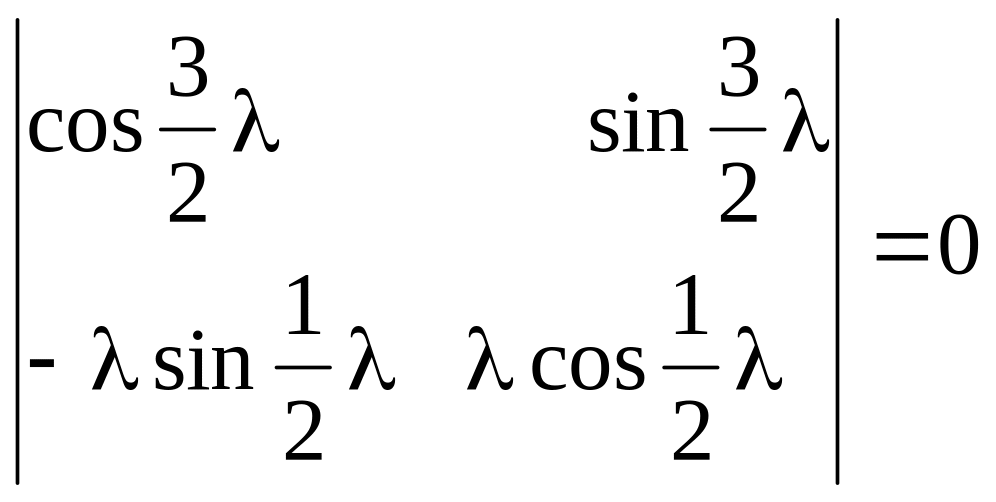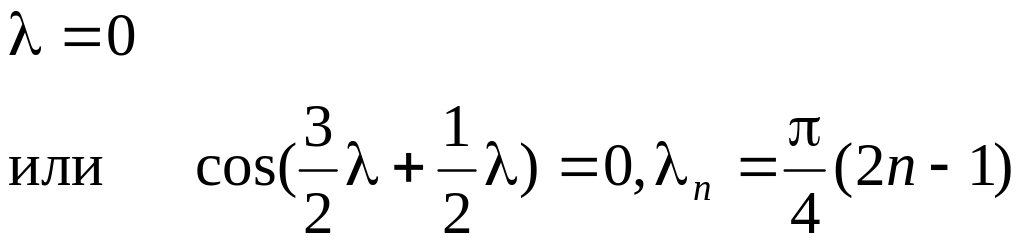собственные значения.
Найдем собственные функции, которые соответствуют данным собственным значениям.
-уравнение,
определяющее форму колебаний.
- значения частоты колебаний
Тема 5. Метод функций Грина решения краевых задач для уравнений эллиптического типа.
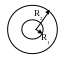
Потенциал на внутренней окружности равен нулю, а потенциал на внешней равен sin ,
Найти U(r,
).
Решение:
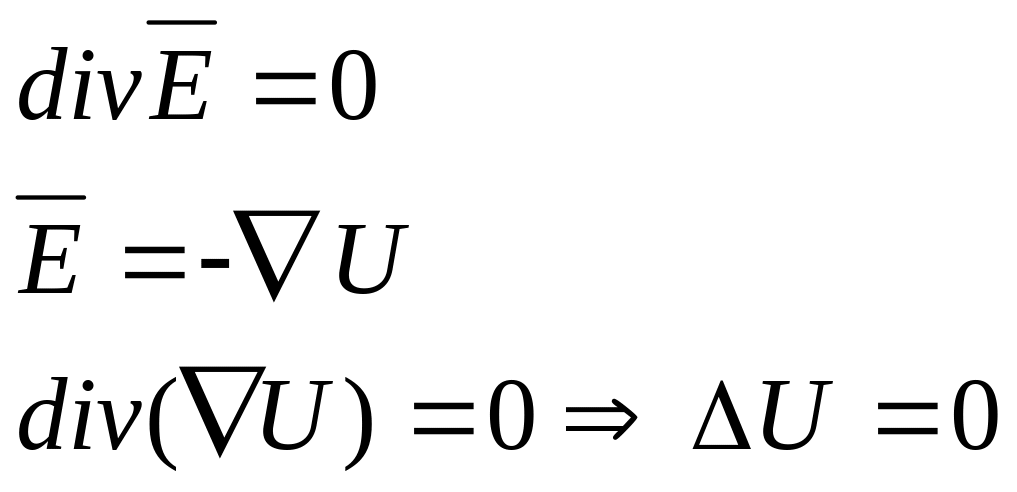
- Граничные условия
Обозначим:
это задача Дирихле в кольце. Решение представляется в виде ряда Фурье.
где коэффициенты определяются из систем:
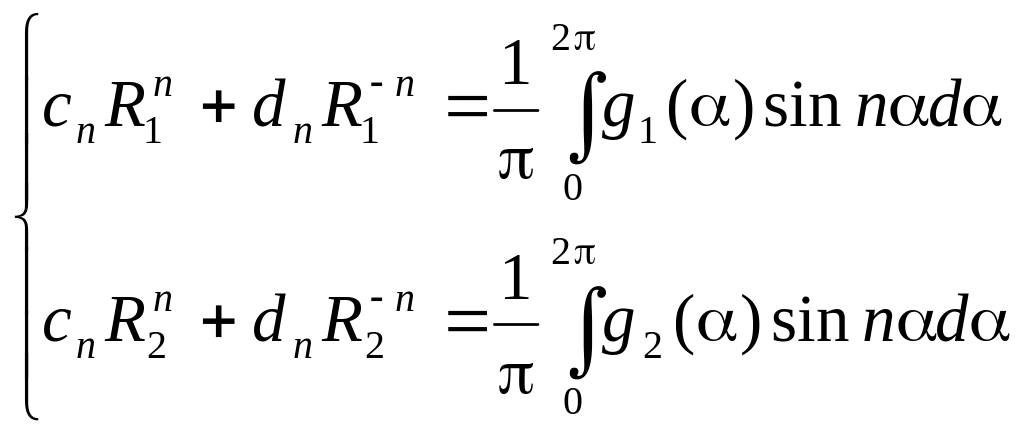
Найдем коэффициенты из граничных условий и условий ортогональности.
=>
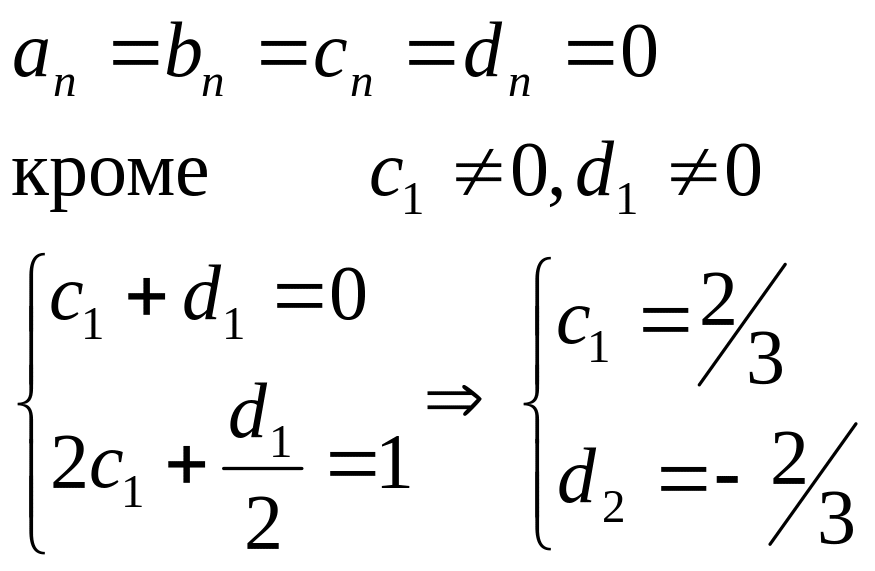
Тогда, подставив все найденные коэффициенты
в общую формулу, получим:
.
БИЛЕТ 16
Тема 3. Метод разделения переменных для решения краевых задач.
Найти закон распределения
температуры в круглой пластине
,
если на границе пластины поддерживается
постоянная нулевая температура. Начальная
температура
.
Решение
Решением данной задачи будет представлено с использованием специальной цилиндрической функции БЕССЕЛЯ
Запишем математическую постановку задачи:
Требуется найти решение
уравнения теплопроводности
для
удовлетворяющим следующим начальным
и краевым условиям.
Запишем Лапласиан в полярной системе координат:
Учтем, что начальные условия не зависят от угла.
Будем решать методом Фурье: Разделим
переменные
,
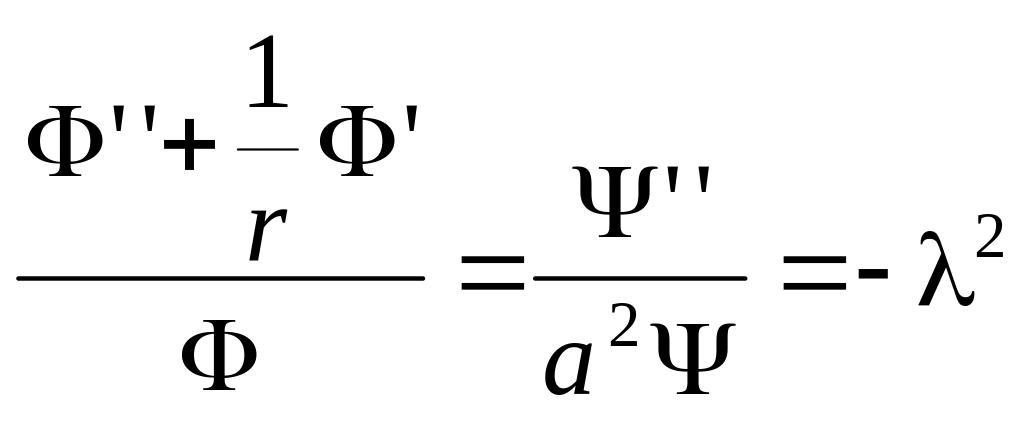
Отсюда
Умножим на
.
- уравнение Бесселя
Граничное условие
Добавляем естественное дополнительное условие:
Общее решение данной задачи представляется с использованием специальной цилиндрической функции – функции Бесселя
Из условия ограниченности получим, что все , т.к. .
Из граничного условия:
,
m=1,2…
Тогда решение:
Собственные функции уравнения:
имеют вид
Тогда решение исходной задачи ищем в форме ряда:
.
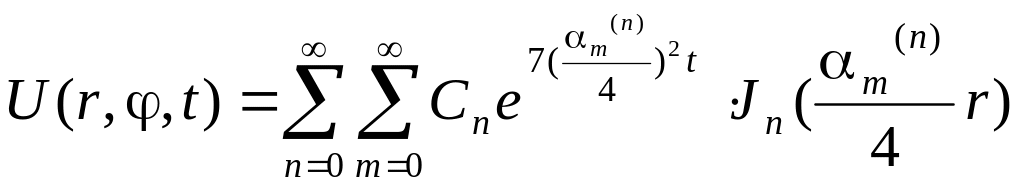Коэффициент ряда
находим, используя начальные условия
и свойство ортогональности функции
Бесселя
Тема 5. Метод функций Грина решения краевых задач для уравнений эллиптического типа.
Потенциал на внутренней окружности равен 3, а потенциал на внешней равен 5,
Найти U(r, ).
Решение
- Граничные условия
Обозначим:
это задача Дирихле в кольце. Решение представляется в виде ряда Фурье.
где коэффициенты определяются из систем:
Найдем коэффициенты из граничных условий и условий ортогональности.
=>
Т.к. условия не зависят от угла, то все
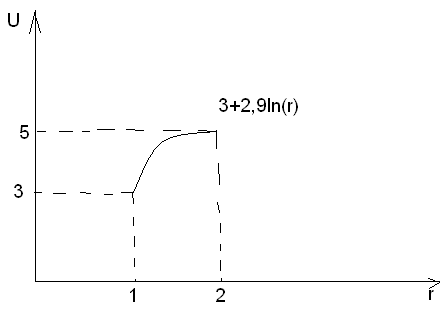
Тогда решение запишется:
,
графически можно представить решение,
см. рис.
БИЛЕТ 17