Тема 1. Задачи, приводящие к уравнениям различных типов.

Поставить краевую задачу для напряжения v(x,t) в проводе длины l, если левый конец этого провода заземлён через сосредоточенное сопротивление R₀ , правый конец заземлён непосредственно.

Решение

Из условия задачи:

• Т.к. правый конец заземлен, то

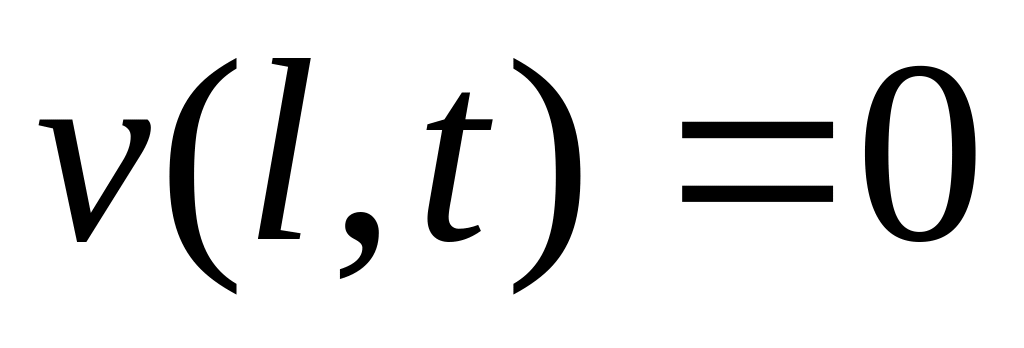
• А если левый конец провода заземлён через сосредоточенное сопротивление R_0, , т.е.

Запишем систему телеграфных уравнений:

Из 1го уравнения получим 2е краевое условие:

Таким образом получили краевые условия 3го типа.

Тема 3. Метод разделения переменных для решения краевых задач.

Решить задачу:

_,

; ;

; .

Решение

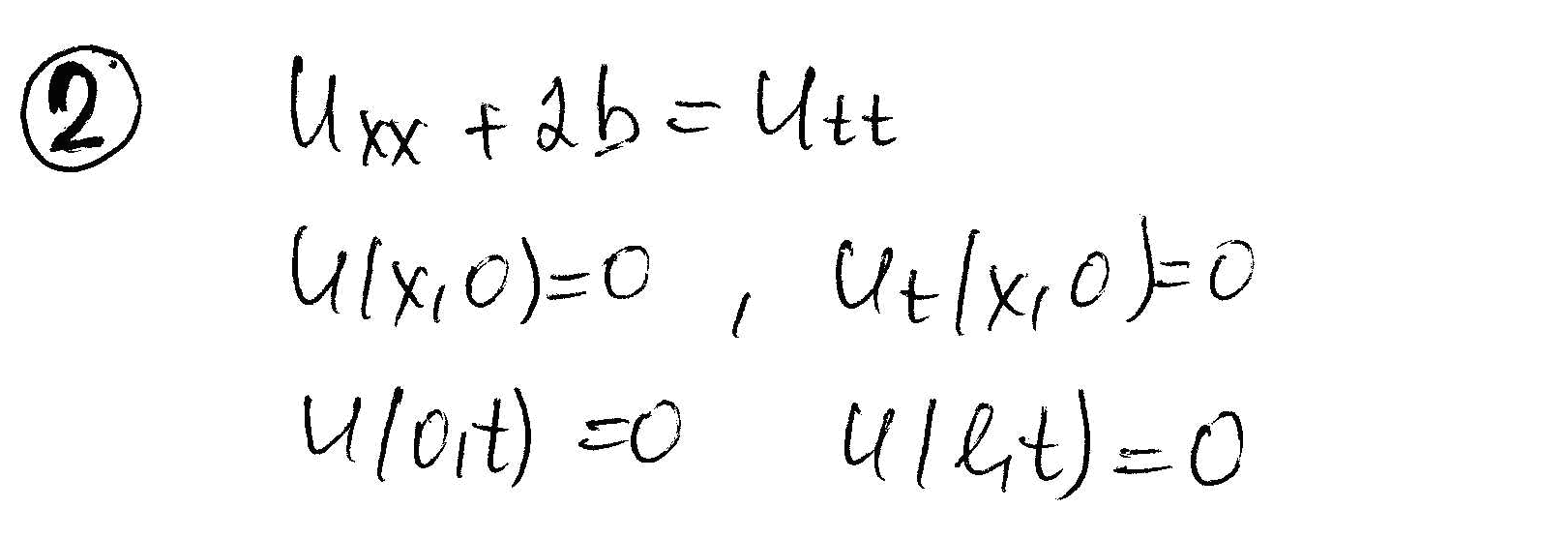
Решаем методом разделения переменных (метод Фурье): .

Второе уравнение:

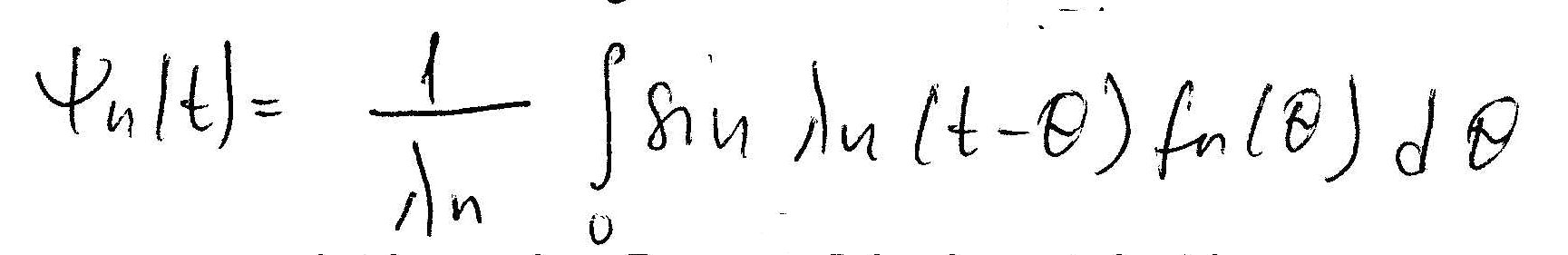
БИЛЕТ 13

Тема 1. Задачи, приводящие к уравнениям различных типов.

Поставить краевую задачу для напряжения v(x,t) в проводе длины l, если левый конец этого провода заземлён через сосредоточенное сопротивление R₀ , правый конец заземлён непосредственно.

Из условия задачи:

• Т.к. правый конец заземлен, то

• А если левый конец провода заземлён через сосредоточенное сопротивление R_0, , т.е.

Запишем систему телеграфных уравнений:

Из 1го уравнения получим 2е краевое условие:

Таким образом получили краевые условия 3го типа.

Тема 3. Метод разделения переменных для решения краевых задач.

Найти закон распределения температуры внутри теплоизолированного стержня длиной l=8, если начальное распределение температуры задано:

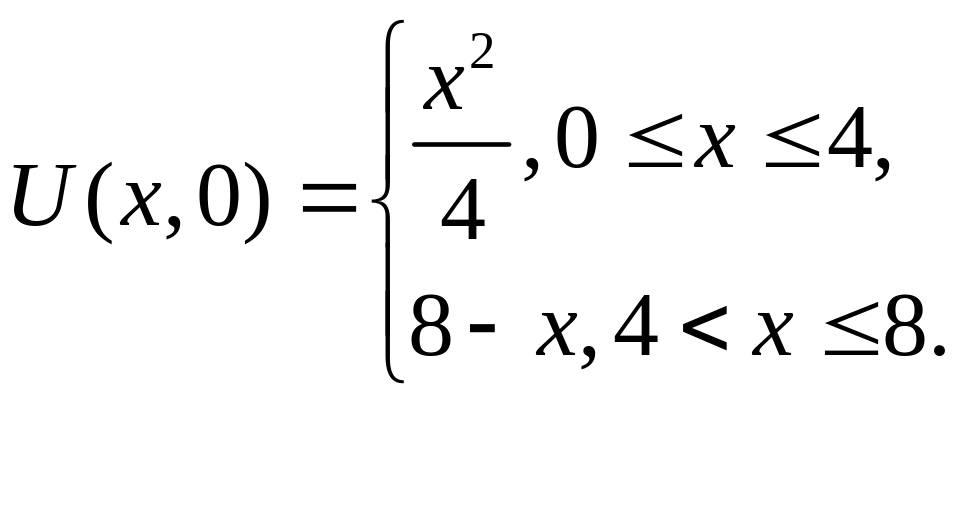
Решение

Имеем уравнение теплопроводности и краевые условия первого типа:

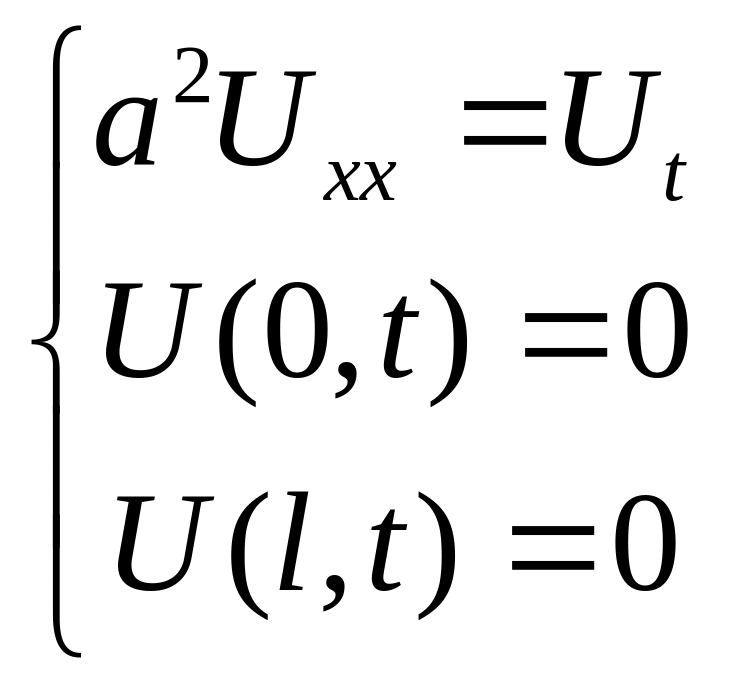
и

Данную задачу будем решать методом Фурье. Решение данной задачи представим в виде произведения: .

Подставляем, преобразуя, разделяем переменные:

, ,

Получаем

- задача Штурма–Лиувилля, где l=8.

Решение этого уравнения в общем виде

Из начальных и краевых условий:

Отсюда собственные функции (с точностью до произвольного постоянного множителя):

.

Из второго уравнения: .

Решение этого ДУ:

Тогда:

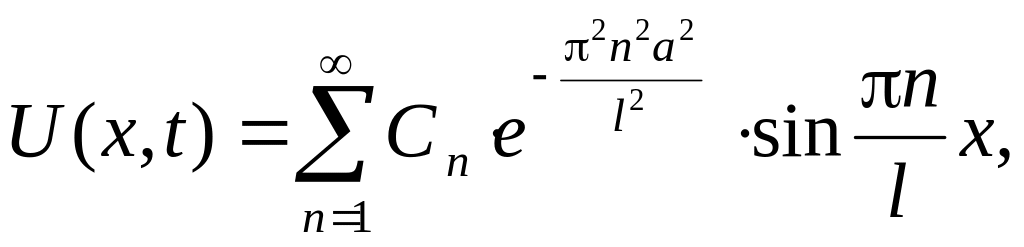
Найдем Cn из начальных условий и принципа ортогональности:

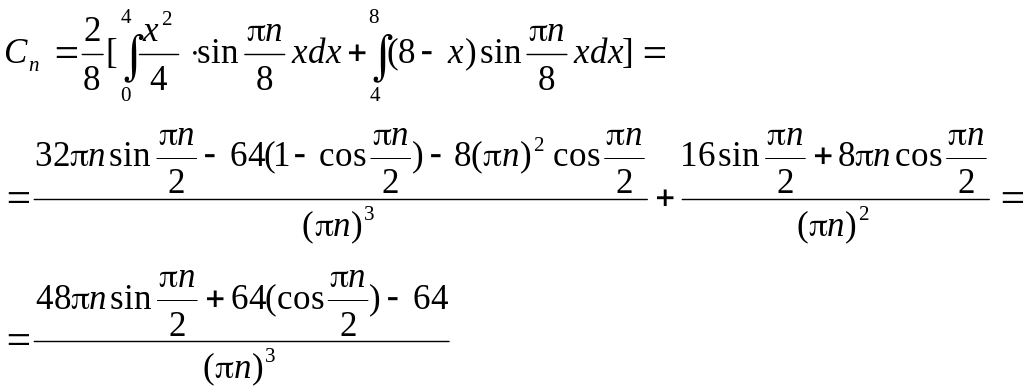
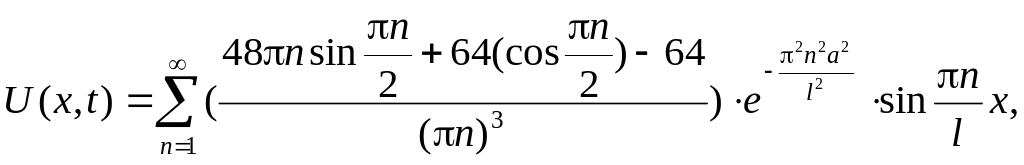
БИЛЕТ 14

Тема 1. Задачи, приводящие к уравнениям различных типов.

Найти и нарисовать область на плоскости (x,y), в которой уравнение

(y²+1)u_xx+xu_xy+u_yy=0 имеет эллиптический тип.

Решение

Для уравнения эллиптического типа необходимо, чтобы

Найдем , известно что: , в нашем случае:

Таким образом:

Область ограничена гиперболой.

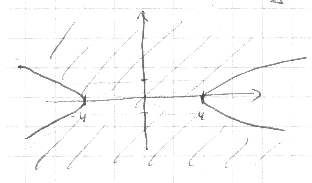
В итоге получим следующую область:

Тема 3. Метод разделения переменных для решения краевых задач.

Концы струны x = 0 и x = L закреплены жестко. Начальное отклонение задано равенством:

Начальные скорости равны нулю. Найти отклонения u(x,t) при t > 0.

Решение

Запишем математическую постановку задачи. Колебания струны можно описать уравнением , это уравнение гиперболического типа. Построим первую краевую задачу:

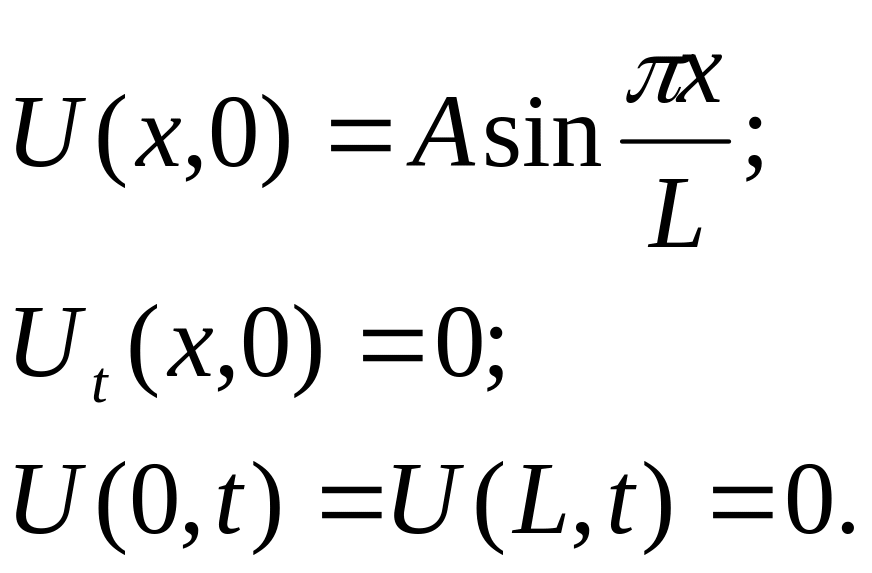
Решаем данную задачу методом Фурье. Решение данной функции представим в виде . Подставив в исходное уравнение, получаем задачу Штурма-Лиувилля

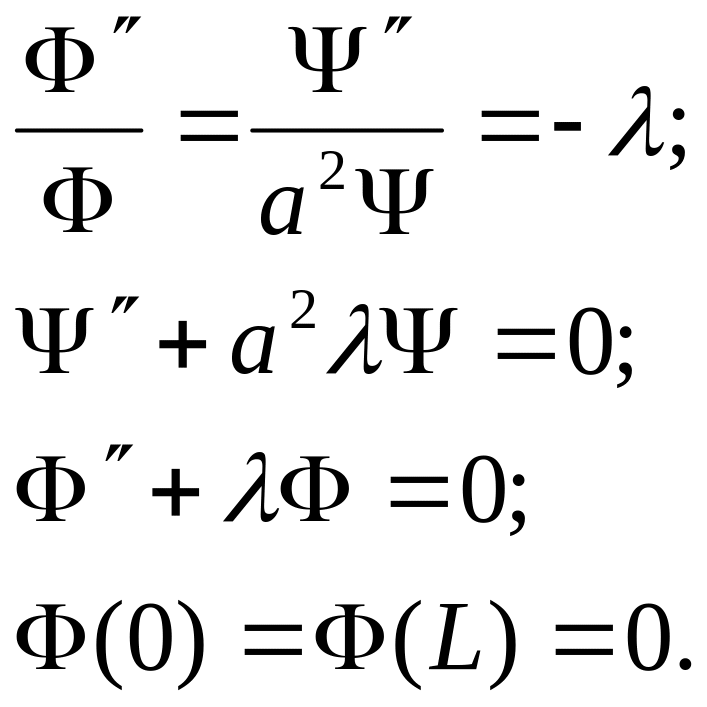
Общее решение задачи можно записать в виде . Подставим численные значения:

Чтобы система имела нетривиальное решение необходимо, чтобы определитель, составленный из коэффициентов при неизвестных значениях:

- собственные значения. Соответствующие им собственные функции: .

Для каждого находим ,

в нашем случае из граничных условий .

Данное выражение в силу свойства ортогональности равно 0 при всех n, кроме n=1, тогда . ,

запишем общее решение

БИЛЕТ 15