Тема 5. Метод функций Грина решения краевых задач для уравнений эллиптического типа.
Решить первую краевую задачу для
уравнения Лапласа
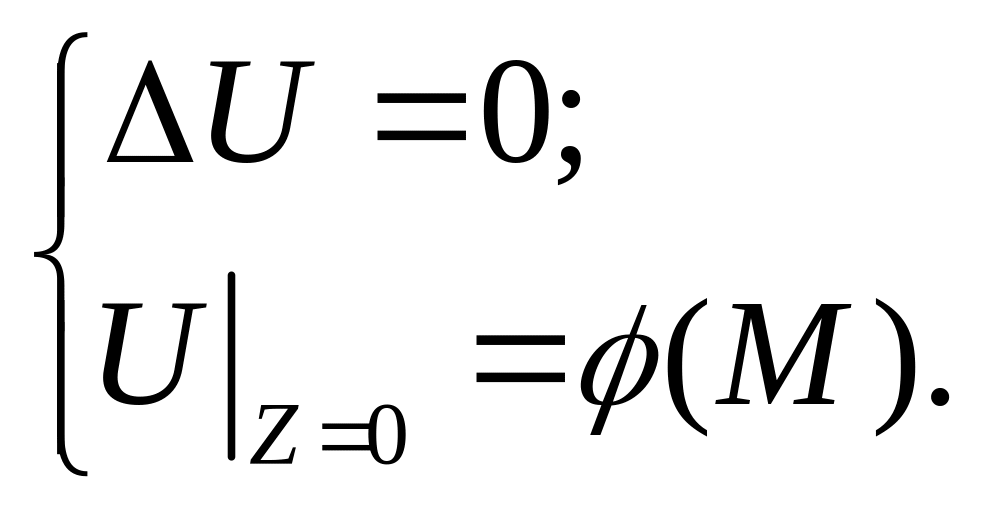
через функцию Грина.
Решение
Решение в общем виде запишем, как
,
с учетом, того, что
=0,
тогда решение примет вид
.
Функция Грина находится из
И она равна
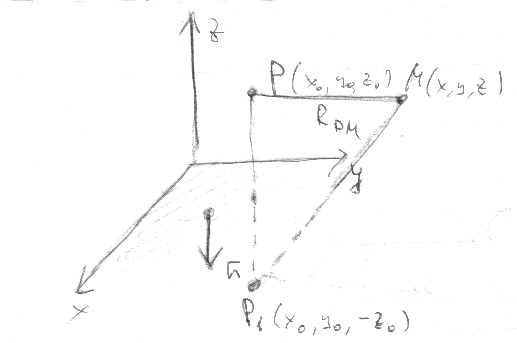
Вычислим
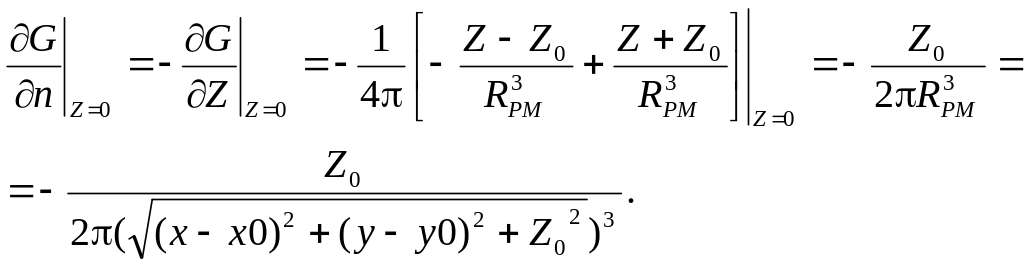
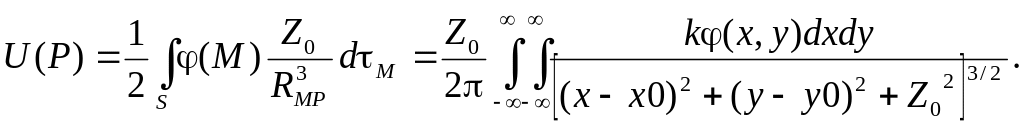
БИЛЕТ 7
Тема 1. Задачи, приводящие к уравнениям различных типов.
Преобразовать уравнение к каноническому виду
Решение
Т.к.
Возможны
3 случая
y=0 – параболический тип. Канонический вид:
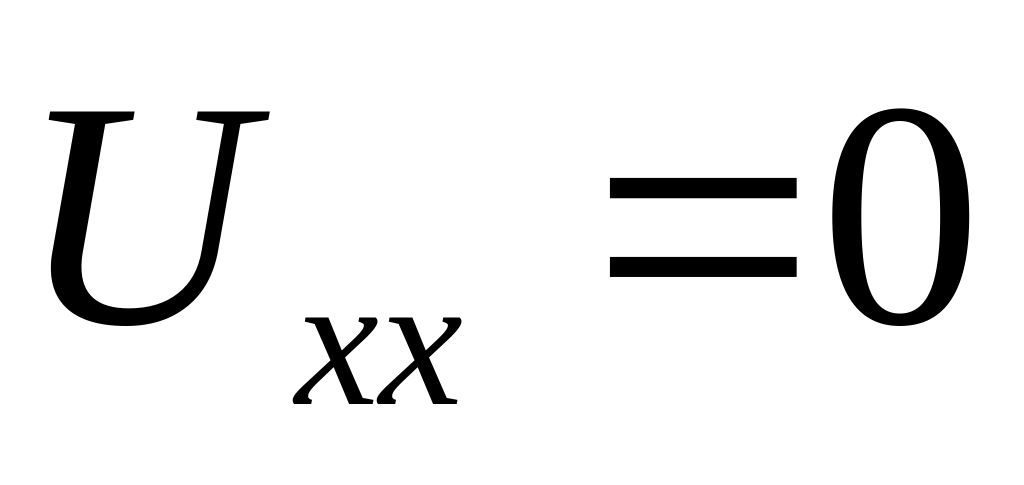
y>0 – гиперболический тип.
Запишем ДУ характеристик:
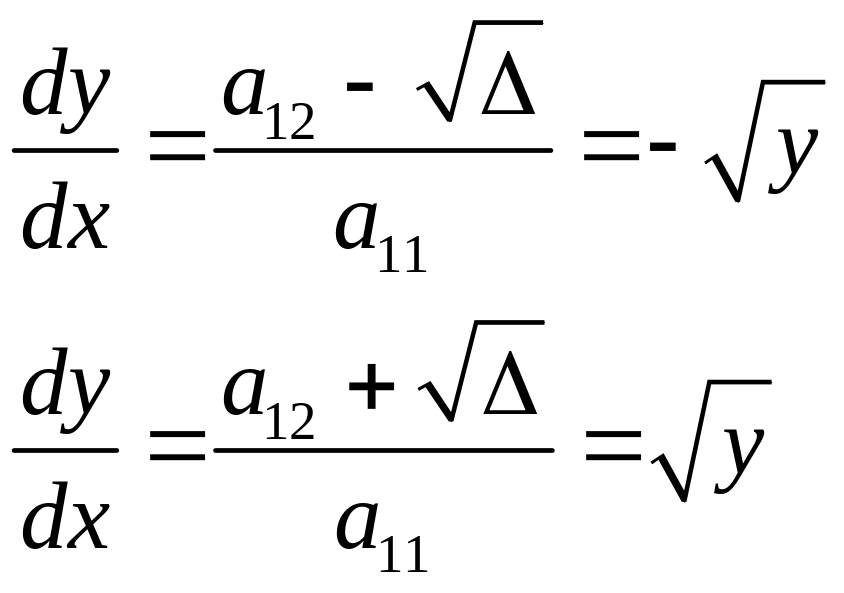
Решение:
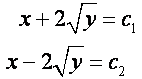
Введем новые переменные:
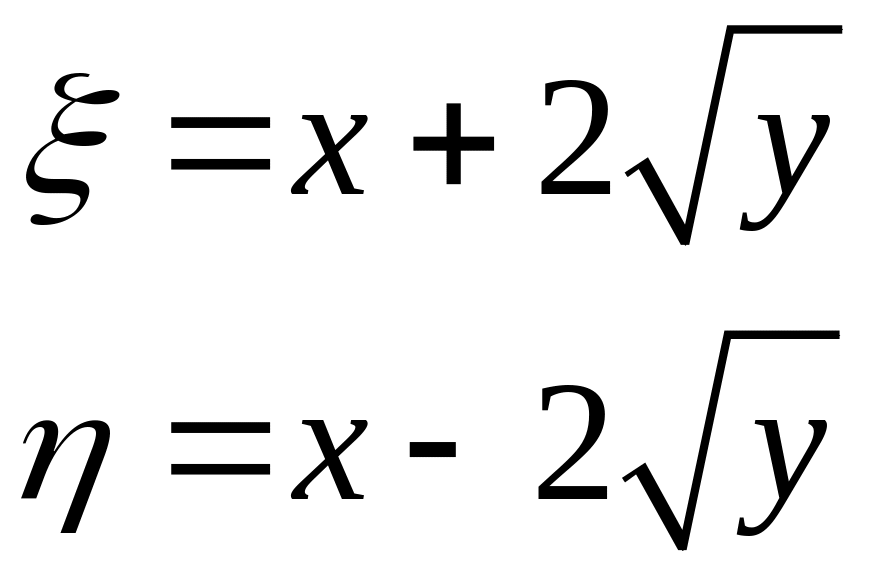
Запишем производные:
Аналогично
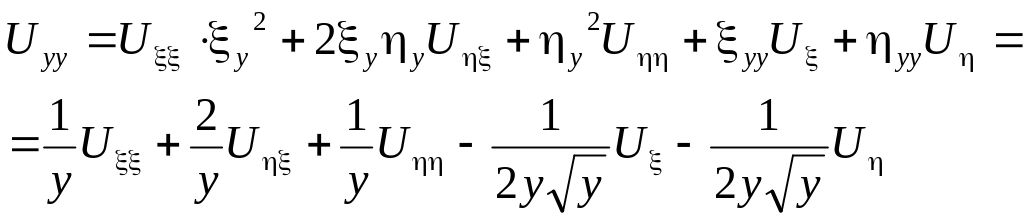
Перепишем левую часть уравнения для новых переменных:
Т.к.
,
то канонический вид уравнения:
y<0 – эллиптический тип.
Запишем ДУ характеристик:
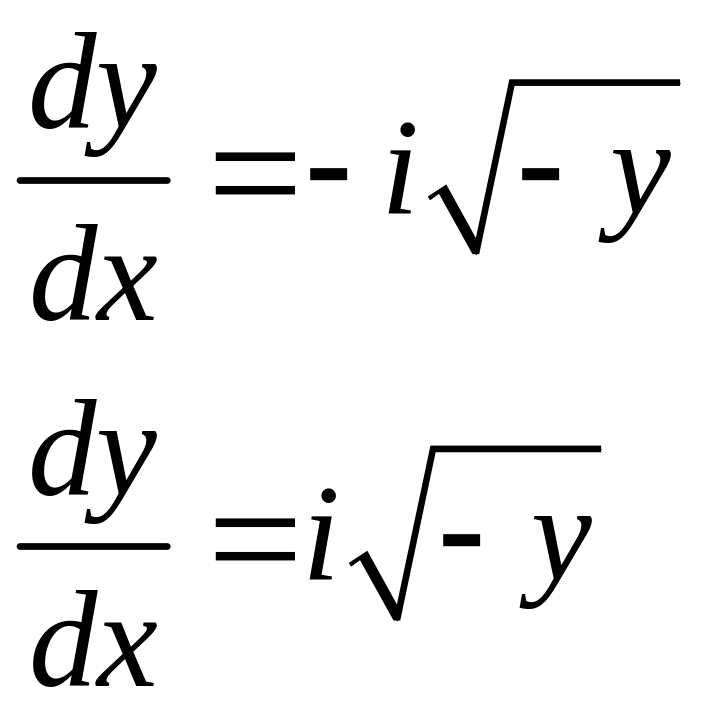
Решение:
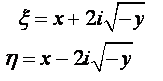
Введем новые переменные:
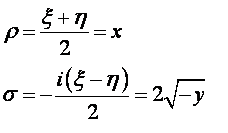
Аналогично запишем производные и уравнение в новых переменных:
-
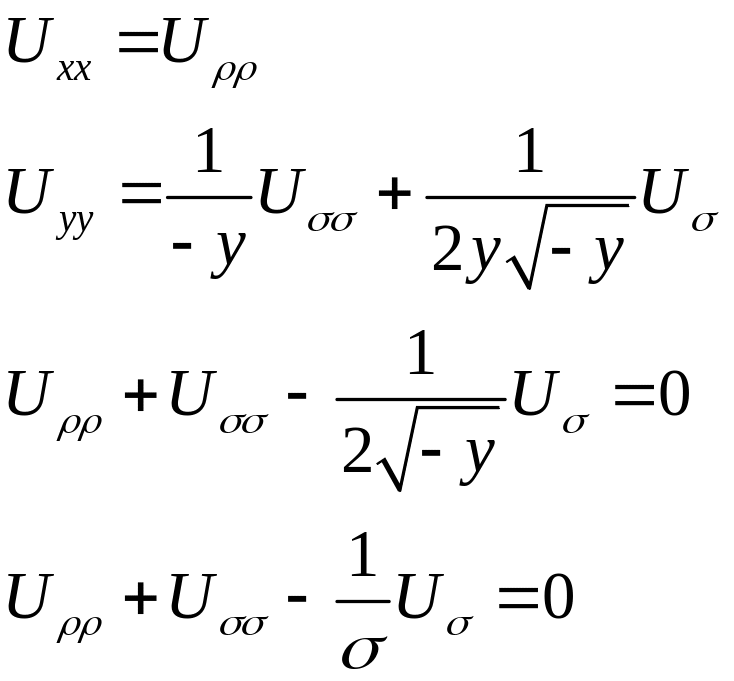канонический вид уравнения:
Тема 3. Метод разделения переменных для решения краевых задач.
Определить форму мыльной пленки между двумя кольцами:
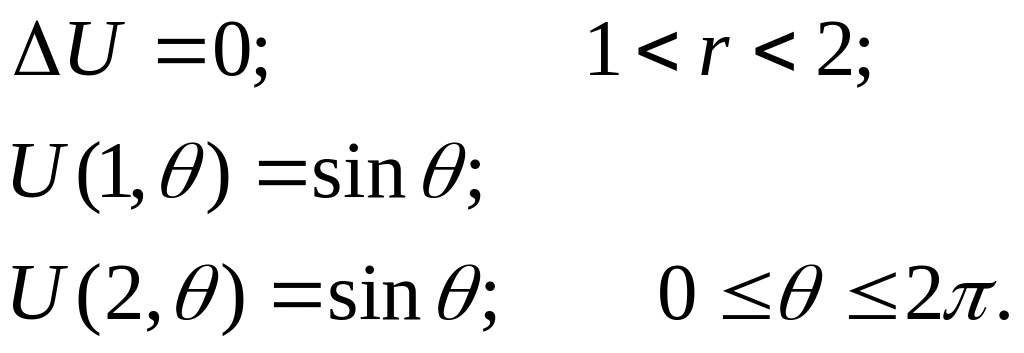
Решение:
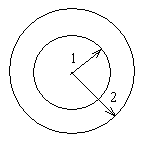
Обозначим:
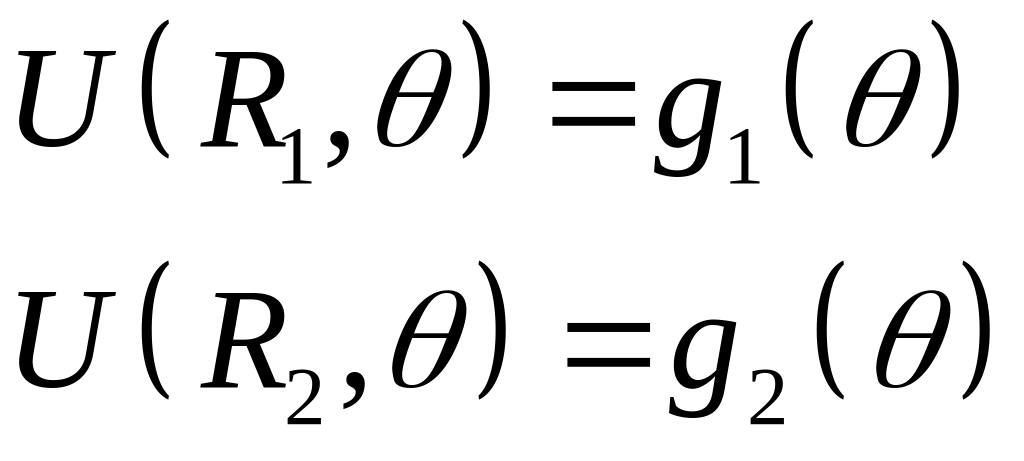
Тогда это задача Дирихле в кольце. Общее решение:
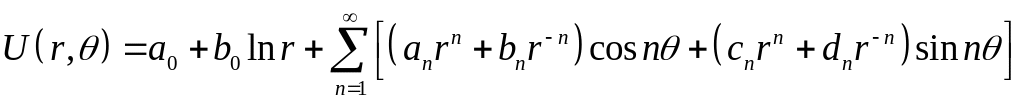
где коэффициенты определяются из систем:
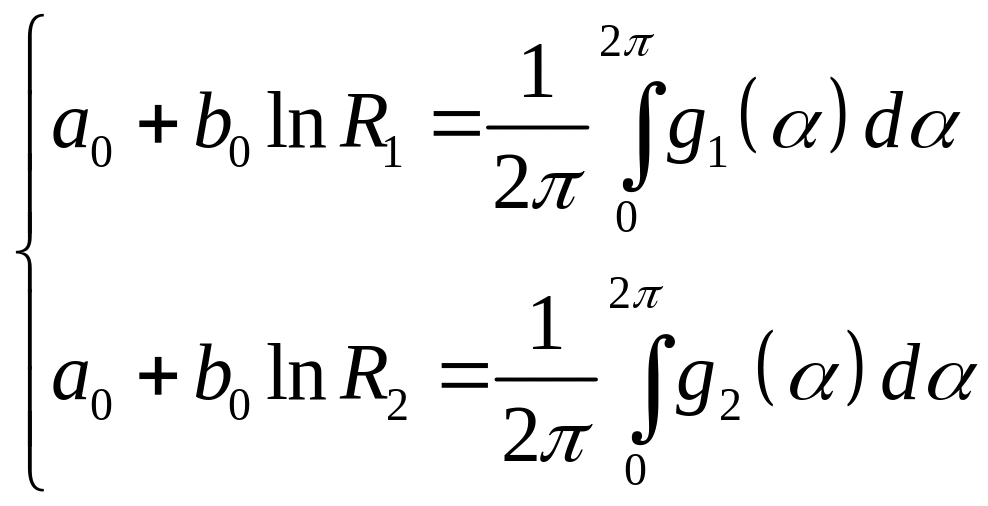
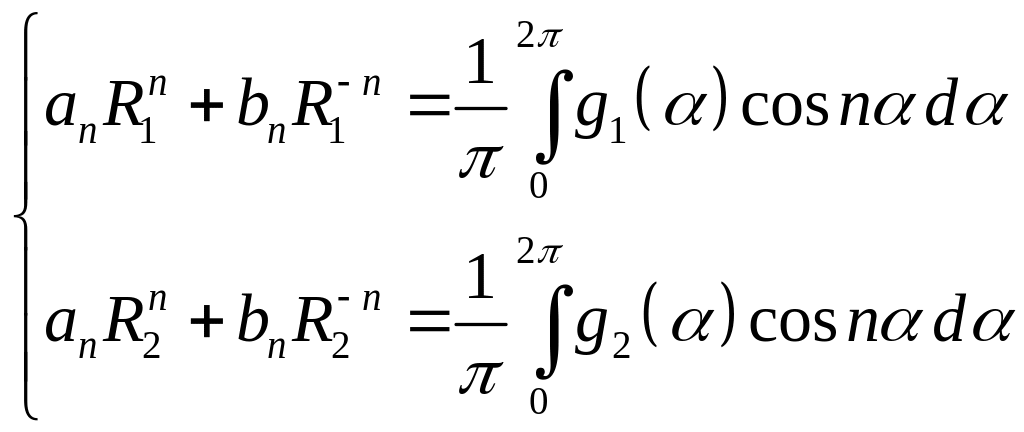
Получаем
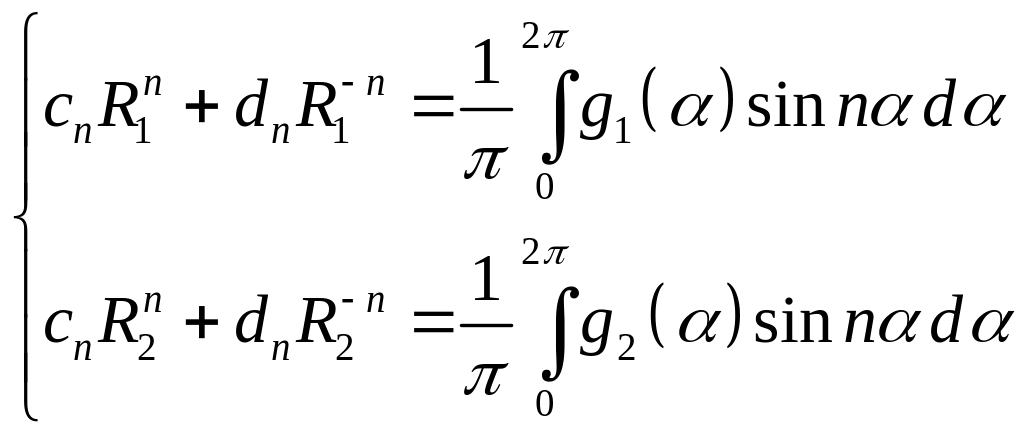
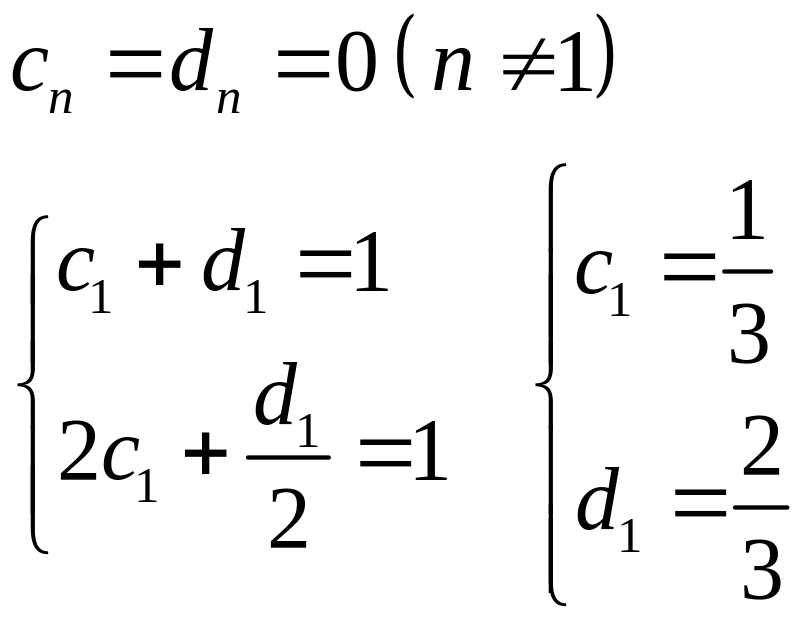
Имеем решение:
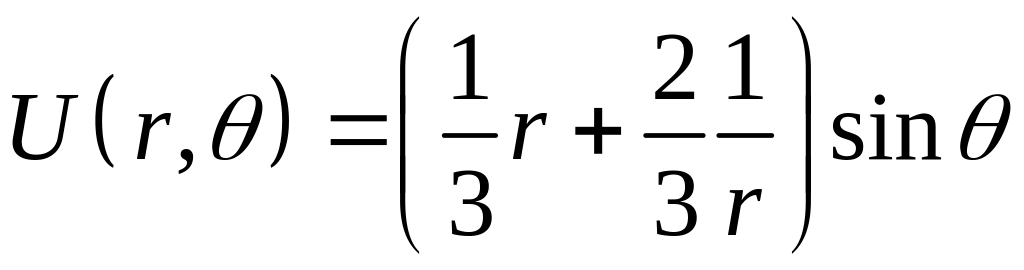
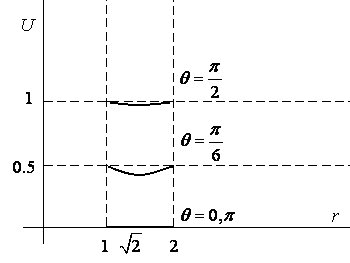
БИЛЕТ 8
Тема 2. Решения задачи Коши для волнового уравнения.
Бесконечная струна возбуждена ударом
так, что начальная скорость отлична от
нуля на отрезке
,
где она принимает постоянное значение
.
Построить профиль струны для моментов
времени
(k = 1,2,3,4,5,6,7,8).
Решение
Уравнение малых поперечных колебаний: .
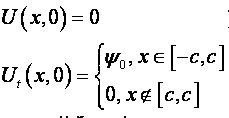
Формула Даламбера:
где
и
Получаем:
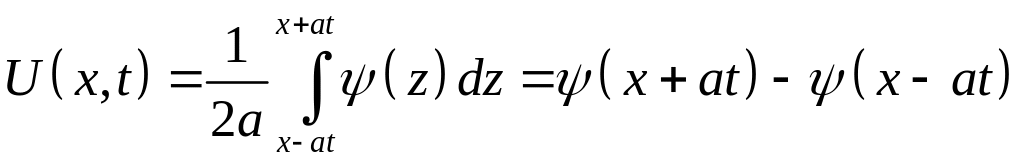
Решение есть суперпозиция 2х волн: прямой и обратной.
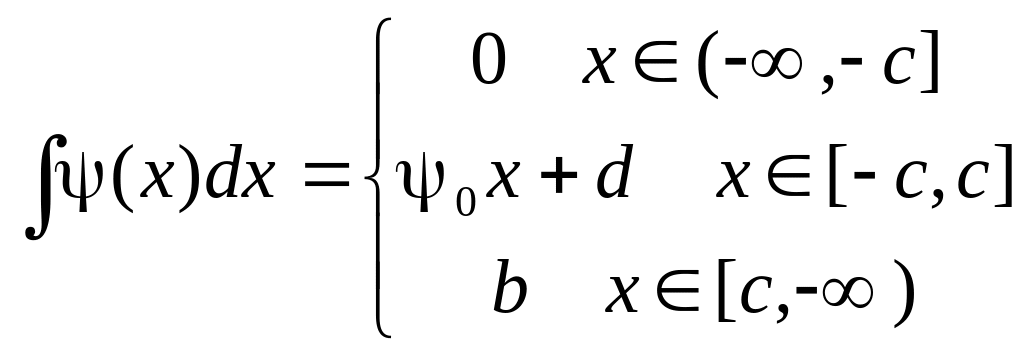
Условия сшивания:
,
в точке x=-c.
,
в точке x=c.
Получаем, что
,
,
в точке x=-c
Тогда решение:
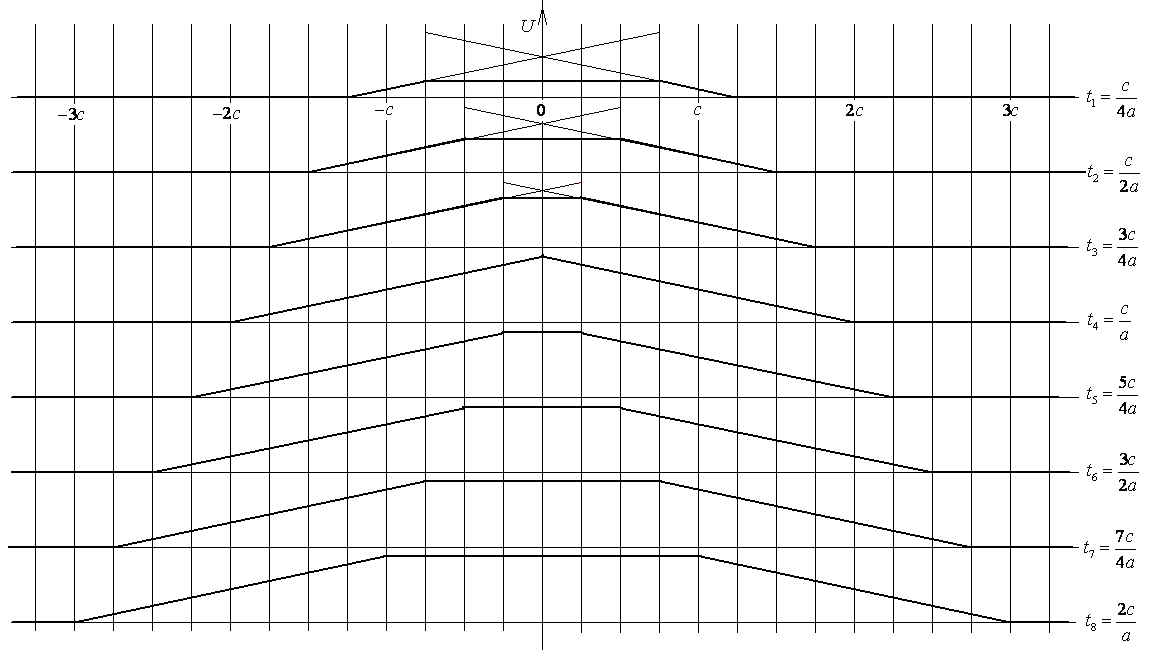
Тема 3. Метод разделения переменных для решения краевых задач.
Струна длины l с закрепленными
концами в начальный момент имеет форму
полуокружности
и
нулевую скорость. Найти зависимость
смещения от координат и времени.
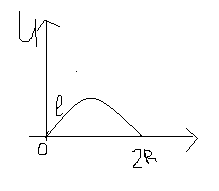
Запишем математическую задачу:
где
Будем искать решение в виде произведения двух функций.
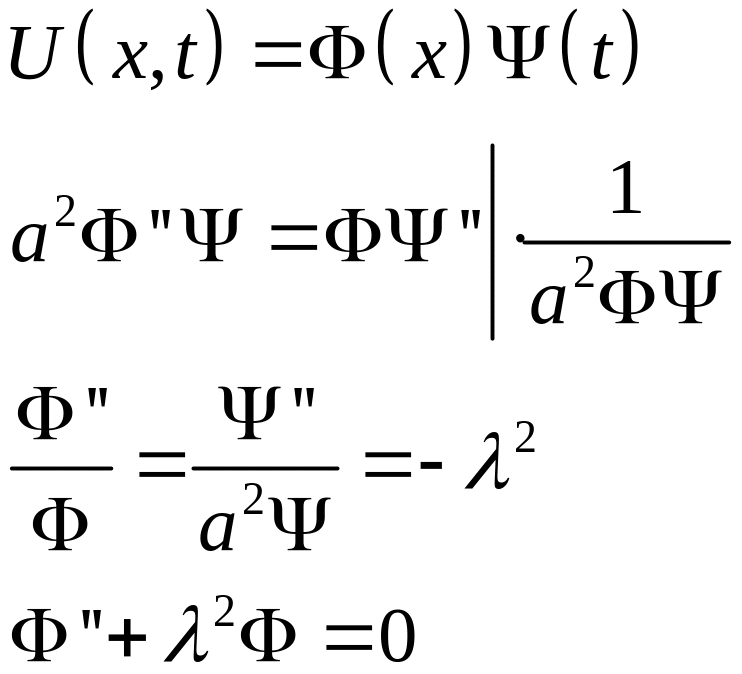
Найдем собственные функции:
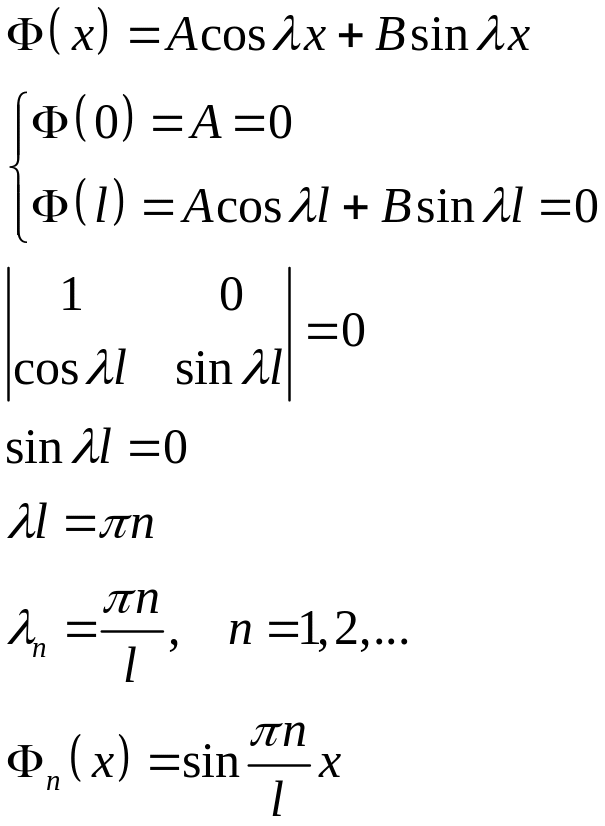
Для второго уравнения:
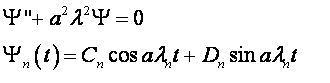
Общее решение:
Из условия ортогональности и граничного условия получаем следующие коэффициенты и
Конечное выражение:
БИЛЕТ 9
Тема 3. Метод разделения переменных для решения краевых задач.
Струна длины l с закрепленными
концами в начальный момент имеет форму
полуокружности
и
нулевую скорость. Найти зависимость
смещения от координат и времени.
Запишем математическую задачу:
где
Будем искать решение в виде произведения двух функций.
Найдем собственные функции:
Для второго уравнения:
Общее решение:
Из условия ортогональности и граничного условия получаем следующие коэффициенты и
Конечное выражение:
Тема 5. Метод функций Грина решения краевых задач для уравнений эллиптического типа.
Решение первой краевой задачи для уравнения Лапласа через функцию Грина.
Решение
Решение в общем виде запишем, как , с учетом, того, что =0, тогда решение примет вид .
Функция Грина находится из
И она равна
Вычислим
БИЛЕТ 10