
- •Вопрос1.Понятие первообразной функции. Неопределенный интеграл. Свойства неопределенного интеграла.
- •Вопрос 4.Определенный интеграл.
- •Вопрос 13. Дифференцируемость функции двух переменных
- •Вопрос 14. Касательная плоскость.
- •Вопрос 15. Дифференциал функции двух переменных. Геометрический смысл дифференциала функции двух переменных.
- •Вопрос 16. Частные производные и дифференциалы функции двух переменных высших порядков.
- •1.Частные производные:
- •2.Дифференциалы высших порядков:
- •Вопрос 17. Локальный экстремум функции двух переменных, необходимые, достаточные условия его существования.
- •Вопрос 18. Производная по направлению. Градиент.
- •Вопрос 19. Понятие числового ряда, его n-ой частичной суммы, сходимости числового ряда и его суммы.
Вопрос1.Понятие первообразной функции. Неопределенный интеграл. Свойства неопределенного интеграла.
1.Функция Ф(х) называется первообразной для функции ф(х) на промежутке Х, если в каждой точке х этого промежутка справедливо равентсво Ф’(x)=f(x). 2.Совокупность всех первообразных для функции ф(х) на промежутке Х называется неопределенным интегралом от функции ф(х) и обозначается ∫f(x)dx = F(x)+C, где С – произвольная постоянная. В записи ∫f(x)dx f(x) подыинтегральной функцией, а f(x)dx – подынтегральным выражением. Нахождение неопределенного интеграла от некоторой функции называется интегрированием этой функции. Операции интегрир. И дифференцирования взаимно обратны. 3.Основные свойства неопределенного интеграла:
(∫f(x)dx)’ = f(x)
d(∫f(x)dx) = f(x)dx
∫dF(x) = F(x)+C
∫αf(x)dx = α∫f(x)dx ,где альфа некоторое число
∫(f(x)±g(x))dx = ∫f(x)dx±∫g(x)dx.
Вопрос 2.Простейшие методы интегрирования. 1.Метод замены переменной. Одним из основных методов интегрирования является метод замены переменной( или метод подстановки), описываемый след формулой: ∫f(x)dx=∫f(φ(t)φ’(t)dt, Где х = - функция, дифференцируемая на рассматриваемом промежутке. Формула показывает, что переходя к новой переменной, достаточно выполнить замену переменной в подынтегральном выражении. По опр. Дифференциала подынтеграл. Выражения левой и правой частей равенства совпадают. Удачная замена переменной позволяет упростить исходный интеграл даже до табличных. 2.Метод интегрирования по частям. Пусть u=u(x) , v=v(x) – дифференцируемые функции. По свойству дифференциала D(uv)=vdu + udv Или Udv=d(uv) _ vdu Интегрируя левую и правую части последнего равенства и учитывая , получаем ∫udv = uv - ∫vdu Формула называется формулой интегрирования по частям для неопределенного интеграла. При ее применении фиксируется разбиение подинтеграл. Выражения искомого интеграла на два сомножителя( и и дв). При переходе к правой части первый из них дифференцируется , второй интегрируется.
Вопрос
3.
Интегрирование
рациональных дробей.
Рациональной
дробью называется отношение двух
многочленов.
Рациональной
дробью называется
выражение вида ![]() ,
где
,
где ![]() ,
,![]() –многочлены
степеней n и m соответственно.
Если
–многочлены
степеней n и m соответственно.
Если ![]() ,
рациональная дробь называется правильной, в
противном случае
,
рациональная дробь называется правильной, в
противном случае ![]() –неправильной.
Если
дробь неправильная, из нее можно выделить
целую часть, разделив числитель на
знаменатель.
Любую
неправильную дробь можно представить
в виде:
–неправильной.
Если
дробь неправильная, из нее можно выделить
целую часть, разделив числитель на
знаменатель.
Любую
неправильную дробь можно представить
в виде:  ,
,
где
P(z) = Q(z) S(z) + R(z),
a R(z) – многочлен, степень которого меньше степени Q(z).
Таким
образом, интегрирование рациональных
дробей сводится к интегрированию
многочленов, то есть степенных функций,
и правильных дробей, так как ![]() является
правильной дробью.
является
правильной дробью.
Простейшими (или элементарными) дробями называются дроби следующих видов:
1) ![]() , 2)
, 2)  , 3)
, 3)  , 4)
, 4) 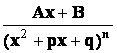
![]() .
.
Каким образом они интегрируются:



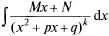 Пусть
Пусть
 правильная :
правильная :


Всякую правильную дробь можно представить в виде суммы простейших дробей (без доказательства).
Следствие
1. Если ![]() -
правильная рациональная дробь, и если
среди корней многочлена
-
правильная рациональная дробь, и если
среди корней многочлена ![]() будут
только простые действительные корни,
то в разложении дроби на сумму простейших
дробей будет присутствовать лишь
простейшие дроби 1-го типа:
будут
только простые действительные корни,
то в разложении дроби на сумму простейших
дробей будет присутствовать лишь
простейшие дроби 1-го типа:

Пример
1. 
Следствие 2. Если - правильная рациональная дробь, и если среди корней многочлена будут только кратные действительные корни, то в разложении дроби на сумму простейших дробей будет присутствовать лишь простейшие дроби 1-го и 2-го типов:


Пример2. 
Следствие 3. Если - правильная рациональная дробь, и если среди корней многочлена будут только простые комплексно - сопряженные корни, то в разложении дроби на сумму простейших дробей будет присутствовать лишь простейшие дроби 3-го типа:

Пример
3. 
Следствие 4. Если - правильная рациональная дробь, и если среди корней многочлена будут только кратные комплексно - сопряженные корни, то в разложении дроби на сумму простейших дробей будет присутствовать лишь простейшие дроби 3-го и 4-го типов:


Пример 4.

Для
определения неизвестных коэффициентов
в приведенных разложениях поступают
следующим образом. Левую и правую часть
разложения ![]() ,
содержащего неизвестные коэффициенты,
умножают на
,
содержащего неизвестные коэффициенты,
умножают на ![]() Получается
равенство двух многочленов. Из него
получают уравнения на искомые коэффициенты,
используя, что:
Получается
равенство двух многочленов. Из него
получают уравнения на искомые коэффициенты,
используя, что:
1. равенство справедливо при любых значениях Х (метод частных значений). В этом случае получается сколько угодно уравнений, любые m из которых позволяют найти неизвестные коэффициенты.
2. совпадают коэффициенты при одинаковых степенях Х (метод неопределенных коэффициентов). В этом случае получается система m – уравнений с m – неизвестными, из которых находят неизвестные коэффициенты.
3. комбинированный метод.
Интегрирование рациональных дробей.
Теорема 6. Неопределенный интеграл от любой рациональной дроби на всяком промежутке, на котором ее знаменатель не равен нулю, существует и выражается через элементарные функции, а именно рациональные дроби, логарифмы и арктангенсы.
Доказательство.
Представим
рациональную дробь
в
виде:  .
При этом последнее слагаемое является
правильной дробью, и по теореме 5 ее
можно представить в виде линейной
комбинации простейших дробей. Таким
образом, интегрирование рациональной
дроби сводится к интегрированию
многочлена S(x) и простейших дробей,
первообразные которых, как было показано,
имеют вид, указанный в теореме.
.
При этом последнее слагаемое является
правильной дробью, и по теореме 5 ее
можно представить в виде линейной
комбинации простейших дробей. Таким
образом, интегрирование рациональной
дроби сводится к интегрированию
многочлена S(x) и простейших дробей,
первообразные которых, как было показано,
имеют вид, указанный в теореме.
Замечание. Основную трудность при этом составляет разложение знаменателя на множители, то есть поиск всех его корней.
