
Распределения непрерывных случайных величин
Равномерное распределение. Непрерывная величина Х распределена равномерно на интервале (a, b), если все ее возможные значения находятся на этом интервале и плотность распределения вероятностей постоянна:
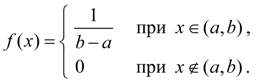 (29)
(29)
Для случайной величины Х , равномерно распределенной в интервале (a, b) (рис. 4), вероятность попадания в любой интервал (x1, x2), лежащий внутри интервала (a, b), равна:
 (30)
(30)
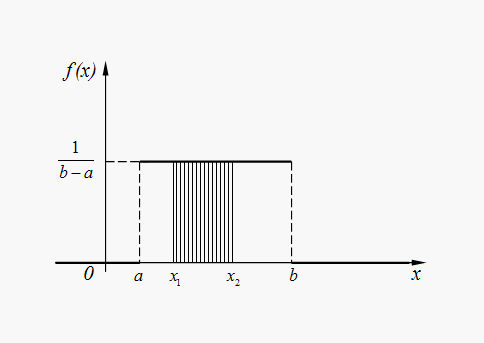 Рис.
4. График плотности равномерного
распределения
Рис.
4. График плотности равномерного
распределения
Примерами
равномерно распределенных величин
являются ошибки округления. Так, если
все табличные значения некоторой функции
округлены до одного и того же разряда
![]() ,
то выбирая наугад табличное значение,
мы считаем, что ошибка округления
выбранного числа есть случайная величина,
равномерно распределенная в интервале
,
то выбирая наугад табличное значение,
мы считаем, что ошибка округления
выбранного числа есть случайная величина,
равномерно распределенная в интервале
![]()
Показательное распределение. Непрерывная случайная величина Х имеет показательное распределение, если плотность распределения ее вероятностей выражается формулой:
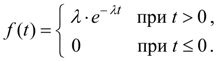 (31)
(31)
График плотности распределения вероятностей (31) представлен на рис. 5.
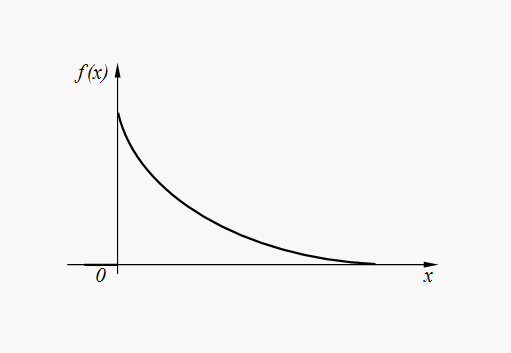 Рис.
5. График плотности показательного
распределения
Рис.
5. График плотности показательного
распределения
Время Т безотказной работы компьютерной системы есть случайная величина, имеющая показательное распределение с параметром λ , физический смысл которого – среднее число отказов в единицу времени, не считая простоев системы для ремонта.
Нормальное (гауссово) распределение. Случайная величина Х имеет нормальное (гауссово) распределение, если плотность распределения ее вероятностей определяется зависимостью:
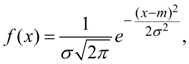 (32)
(32)
где
m
= M(X)
,
![]() .
.
При
![]() нормальное
распределение называется стандартным.
нормальное
распределение называется стандартным.
График плотности нормального распределения (32) представлен на рис. 6.
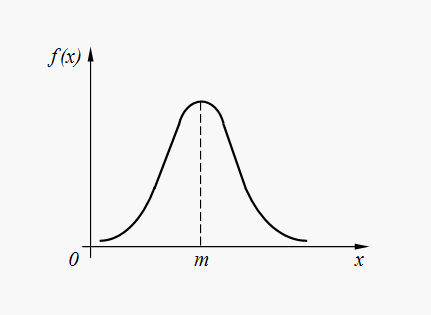 Рис.
6. График плотности нормального
распределения
Рис.
6. График плотности нормального
распределения
Нормальное распределение является наиболее часто встречающимся в различных случайных явлениях природы. Так, ошибки выполнения команд автоматизированным устройством, ошибки вывода космического корабля в заданную точку пространства, ошибки параметров компьютерных систем и т.д. в большинстве случаев имеют нормальное или близкое к нормальному распределение. Более того, случайные величины, образованные суммированием большого количества случайных слагаемых, распределены практически по нормальному закону.
Гамма-распределение. Случайная величина Х имеет гамма-распределение, если плотность распределения ее вероятностей выражается формулой:
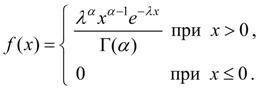 (33)
(33)
где
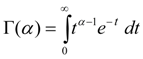 –
гамма-функция Эйлера.
–
гамма-функция Эйлера.
Основные свойства гамма-функции:

Параметры
![]() –
любые положительные числа. Гамма-распределение
является также распределением
Пирсона типа III
[3]. При
–
любые положительные числа. Гамма-распределение
является также распределением
Пирсона типа III
[3]. При
![]() гамма-распределение
превращается в показательное распределение
с параметром λ,
так как Г(1) = 1. Гамма-распределение широко
используется в математической статистике.
Hа рис. 7 представлены графики плотности
гамма-распределения (33) при
гамма-распределение
превращается в показательное распределение
с параметром λ,
так как Г(1) = 1. Гамма-распределение широко
используется в математической статистике.
Hа рис. 7 представлены графики плотности
гамма-распределения (33) при ![]() .
.
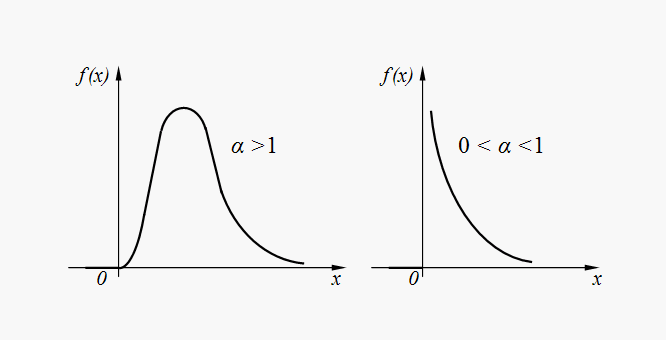 Рис.
7. Графики плотности гамма-распределения
Рис.
7. Графики плотности гамма-распределения
Системы случайных величин
Существенный интерес в математической статистике представляет рассмотрение системы двух и более случайных величин и их статистическая взаимосвязь друг с другом.
По аналогии с рядом распределения одной дискретной величины Х для двух дискретных случайных величин X и Y строится матрица распределения – прямоугольная таблица, в которой записаны все вероятности pi j = P{ X = xi , Y = yj } , i = 1, … , n; j = 1,…, m.
События (или опыты) называются независимыми, если вероятность появления (исхода) каждого из них не зависит от того, какие события (исходы) имели место в других случаях (опытах).
Две случайные величины X и Y называются независимыми, если независимы все связанные с ними события: например, {X < а} и {Y < b} или {X = xi} и {Y = yi} и т.д.
В терминах законов распределения справедливо также следующее определение: две случайные величины X и Y называются независимыми, если закон распределения каждой из них не зависит от принятого значения другой.
Совместной функцией распределения системы двух случайных величин ( X, Y ) называется вероятность совместного выполнения неравенств X < х и Y < у :
![]() (34)
(34)
Событие![]() означает
произведение (совместное выполнение)
событий {X
< х}
и {Y
< у}.
Геометрической интерпретацией
совместной функции распределения F
(
x,
y)
является вероятность попадания случайной
точки (
X,
Y
)
на плоскости внутрь бесконечного
квадранта с вершиной в точке (x,
y)
(заштрихованная область на рис. 8).
означает
произведение (совместное выполнение)
событий {X
< х}
и {Y
< у}.
Геометрической интерпретацией
совместной функции распределения F
(
x,
y)
является вероятность попадания случайной
точки (
X,
Y
)
на плоскости внутрь бесконечного
квадранта с вершиной в точке (x,
y)
(заштрихованная область на рис. 8).
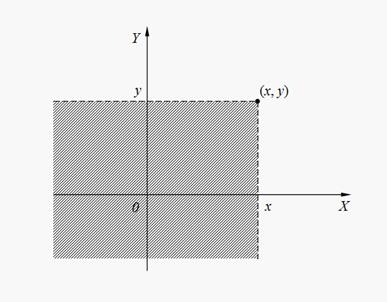
Рис. 8. Геометрическая интерпретация совместной функции распределения F(x, y)
Основные свойства совместной функции распределения:
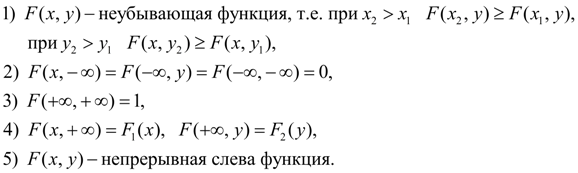 (35)
(35)
Здесь
![]()
Система
двух случайных величин (
X,
Y
)
называется непрерывной,
если ее совместная функция распределения
F
(x,
y)
– непрерывная функция, дифференцируемая
по каждому аргументу, у которой существует
вторая смешанная частная производная
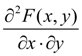 .
Обе случайные величины X
и Y
– непрерывны. Тогда функция
.
Обе случайные величины X
и Y
– непрерывны. Тогда функция
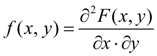 (36)
(36)
называется совместной плотностью распределения системы двух случайных величин ( X, Y ).
Основные свойства совместной плотности распределения:
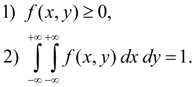 (37)
(37)
В качестве числовых характеристик системы двух случайных величин X и Y обычно рассматриваются начальные и центральные моменты различных порядков. Порядком момента называется сумма его индексов k + s.
Начальным моментом порядка k + s системы двух случайных величин X и Y называется математическое ожидание произведения X k на Y s :
![]() (38)
(38)
Центральным моментом порядка k + s системы двух случайных величин ( X, Y ) называется математическое ожидание произведения (X–mx )k на (Y–my )s :
![]() (39)
(39)
где mx = М (Х), my = М (Y).
Для системы дискретных случайных величин X и Y :
 (40)
(40)
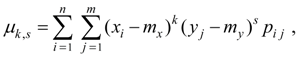 (41)
(41)
где рi j = Р { Х =xi , Y = yj }.
Для системы непрерывных случайных величин X и Y :
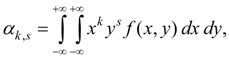 (42)
(42)
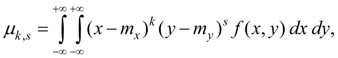 (43)
(43)
где f ( x, y ) – совместная плотность распределения случайных величин X и Y.
В инженерных приложениях математической статистики чаще всего используются моменты первого и второго порядков.
Начальные моменты первого порядка
![]() (44)
(44)
являются математическими ожиданиями случайных величин X и Y.
Центральные моменты первого порядка всегда равны нулю:
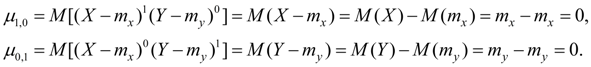 (45)
(45)
Начальные моменты второго порядка:
 (46)
(46)
Центральные моменты второго порядка:
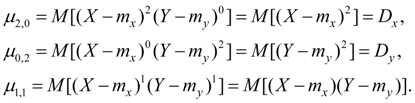 (47)
(47)
Здесь Dx , Dy – дисперсии случайных величин X и Y.
Центральный
момент второго порядка
![]() называется
ковариацией
случайных величин X
и Y.
Обозначим его
называется
ковариацией
случайных величин X
и Y.
Обозначим его
![]() :
:
![]() .
(48)
.
(48)
Из определения ковариации (48) следует:
![]() (49)
(49)
Дисперсия случайной величины является по существу частным случаем ковариации:
![]() (50)
(50)
По определению ковариации (48) получим:
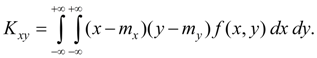 (51)
(51)
Ковариация
двух случайных величин X
и Y
характеризует степень их зависимости
и меру рассеивания вокруг точки
![]() .
Часто бывает удобно выразить ковариацию
в
виде:
.
Часто бывает удобно выразить ковариацию
в
виде:
![]() (52)
(52)
Выражение (52) вытекает из определения ковариации (48).
Размерность ковариации равна произведению размерностей случайных величин X и Y.
Безразмерная величина, характеризующая только зависимость случайных величин X и Y, а не разброс:
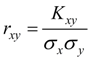 (53)
(53)
называется коэффициентом корреляции случайных величин X и Y. Этот параметр характеризует степень линейной зависимости случайных
величин
X
и Y.
Для любых двух случайных величин X
и Y
коэффициент корреляции
![]() .
Если
.
Если
![]() ,
то линейная зависимость между X
и Y
возрастающая, если
,
то линейная зависимость между X
и Y
возрастающая, если
![]() ,
то линейная зависимость междуX
и Y
убывающая, при
,
то линейная зависимость междуX
и Y
убывающая, при
![]() линейной
зависимости между X
и Y
нет. При
линейной
зависимости между X
и Y
нет. При
![]() случайные
величины X
и Y
называются коррелированными, при
–
некоррелированными. Отсутствие линейной
корреляции не означает отсутствие любой
другой зависимости между X
и Y.
Если имеет место жесткая линейная
зависимость Y
= aX+
b
, то
случайные
величины X
и Y
называются коррелированными, при
–
некоррелированными. Отсутствие линейной
корреляции не означает отсутствие любой
другой зависимости между X
и Y.
Если имеет место жесткая линейная
зависимость Y
= aX+
b
, то
![]() при
а
> 0 и
при
а
> 0 и
![]() при
а
< 0.
при
а
< 0.
