3)Ступенчатый вид и вид Гаусса.

Ступенчатый вид: 1- элементарными преобразованиями строк матрицы называются преобразования след 3 типов: а) перестановка местами 2х строк матрицы

Б) замена строки суммой этой строки и некоторой другой, вспомогательной, предварительно умноженной на какое-либо число Л(альфа).

В) умножение строки на нулевое число Л(альфа). условное обозначение (Л), где множитель (Л) ставится рядом с преобразуемой строкой.

2- опорным элементом строки матрицы называется первый слева нулевой элемент этой строки. Если строка нулевая, то опорного элемента у нее нет.

3- матрица называется ступенчатой, если выполнены след условия: -если какая-то строка матрицы нулевая, то все последующие строки-нулевые -опорный элемент в каждой послед строке расположен правее, чем в пред строке

4- говорят, что ступенчатая матрица имеет вид Гаусса, если: -все опорные элементы=1 -над опорными элементами стоят только 0

5- Матрицы А1 и А2, построенные по матрице А с помощью элементарных преобразований, называются, соответственно, ступенчатым видом матрицыА и видом гаусса матрицы А.

6- у матрицы ступенчатый вид и вид Гаусса не единствен. Набор базисных строк и базисных столбцов матрицы также не явл инвариантом этйо матрицы. Однако кол-во базисных строк и базисных столбцов постоянно.

4)Определение ранга матрицы.

Рангом матрицы А называется число ненулевых строк в ступенчатом виде этой матрицы. обозначение r(A) или rangA.

Ранг матрицы не меняется при применении к матрице А элементарных преобразований, не зависит от способа приведения матрицы к ступенчатому виду.

5)Система линейных алгебраических уравнений. Теорема Кронекера-Канелли.

Система линейных алгебраических уравнений с неизвестными — это система уравнений вида

Здесь  — неизвестные, которые надо определить. Коэффициенты системы и её свободные члены предполагаются известными. Индексы коэффициента системы обозначают номера уравнения  и неизвестного  , при котором стоит этот коэффициент.

Система называется однородной, если все её свободные члены равны нулю, , иначе — неоднородной.

Система называется квадратной, если число  уравнений равно числу  неизвестных.

Решение системы уравнений — совокупность чисел , таких что подстановка каждого  вместо  в систему обращает все её уравнения в тождества.

Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если у нее нет ни одного решения. Совместная система может иметь одно или более решений.

Решения и совместной системы называются различными, если нарушается хотя бы одно из равенств:

Совместная система называется определенной, если она имеет единственное решение; если же у нее есть хотя бы два различных решения, то она называется неопределенной. Если уравнений больше, чем неизвестных, она называется переопределённой.

Пример системы линейных уравнений

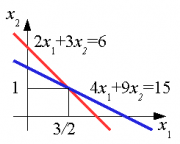
Графическое решение системы линейных уравнений

Система из двух уравнений с двумя неизвестными имеет вид

Чтобы найти неизвестные нужно решить верхнее уравнение относительно  : а затем подставить полученное решение в нижнее уравнение: Получено решение .

Данную систему можно наглядно изобразить на графике в виде двух прямых. Точка с координатами является ее решением.

Методы решения

Прямые (или точные) методы решения СЛАУ позволяют найти решение за определенное количество шагов. К прямым методам относятся метод Гаусса, метод Гаусса — Жордана, метод Крамера, матричный метод и метод прогонки (для трёхдиагональных матриц).

Итерационные методы основаны на использовании повторяющегося процесса. Они позволяют получить решение в результате последовательных приближений. К итерационным методам относятся метод Якоби (метод простой итерации), метод Гаусса — Зейделя, метод релаксации и многосеточный метод.

Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений: Система линейных алгебраических уравненийсовместна тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных. Доказательство (условия совместности системы)

Необходимость

Пусть система совместна. Тогда существуют числа такие, что . Следовательно, столбец является линейной комбинацией столбцов матрицы . Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что .

Достаточность

Пусть . Возьмем в матрице какой-нибудь базисный минор. Так как , то он же и будет базисным минором и матрицы . Тогда согласно теореме о базисном миноре последний столбец матрицы будет линейной комбинацией базисных столбцов, то есть столбцов матрицы . Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы .

Следствия

• Количество главных переменных системы равно рангу системы.

• Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных.