Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Российский государственный социальный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Matematika_Gorodskoy_kadastr_Logistika_1_chas

.pdf

Скачиваний:

Добавлен:

12.06.2015

Размер:

659.01 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Государственное образовательное учреждение высшего профессионального образования

«РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ»

Утверждено на заседании кафедры

прикладной математики и вычислительной техники

20.05.2011 г.

Математика (1-й семестр)

Методические указания для практических работ студентов специальности «Городской кадастр, Логистика»

Ростов-на-Дону

2011

УДК 51(075.8)

Математика (1-й семестр): методические указания для практических работ студентов специальности «Городской кадастр, Логистика». – Ростов н/Д: Рост. гос. строит. ун-т, 2011. – 16 с.

Приводятся в краткой форме основные понятия по разделам математики, которые изучаются в 1-м семестре. Предназначены для практических работ бакалавров специальности «Городской кадастр, Логистика» как очной, так и заочной форм обучения. Направление подготовки 120700 «Землеустройство и кадастр». Профиль подготовки «Городской кадастр, Логистика».

Электронная версия методических указаний находится в библиотеке,

ауд. 224.

УДК 51(075.8)

Составитель: к. ф.-м. н., доц. Н.П. Красий

Редактор Н.Е. Гладких Доп. план 2011 г., поз. 52.

Подписано в печать 20.06.11. Формат 60 84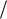16 . Бумага писчая. Ризограф. Уч.-изд.л. 1,7. Тираж 100 экз. Заказ 208

Редакционно-издательский центр Ростовского государственного строительного университета

344022, Ростов-на-Дону, ул. Социалистическая, 162.

Ростовский государственный строительный университет, 2011

МАТРИЦЫ Матрицей называется таблица чисел. Обозначается А или с указанием

размерности Am n , где m n – размерность: m – количество строк матрицы, а п

– количество столбцов.

Элементы матрицы обозначаются aij , где i показывает номер строки, в которой находится элемент, а j – номер столбца.

			a	a	...	a
			11	12		1n
Общий вид матрицы A	:	A	a21	a22	...	a2n	.
Общий вид матрицы A	:	A	... ...			...	.
m n		m n	... ...		...	...

				am2	...
			am1	am2	...	amn

Если количество строк матрицы совпадает с количеством столбцов и равно п, то матрица называется квадратной матрицей п-го порядка.

Элементы квадратной матрицы, индексы которых одинаковы – aii , называются

лежащими на главной диагонали или главной диагональю. Другая диагональ квадратной матрицы называется побочной.

ОПРЕДЕЛИТЕЛИ МАТРИЦ

Определителем матрицы А второго порядка является число, равное разности произведений элементов главной и побочной диагоналей:

					A			a11			a12			a a							a a					,	1 7			1 2 7 3 19 .
					A			a11			a12			a a							a a					,	1 7			1 2 7 3 19 .
								a21			a22				11				22				12	21			3	2
								a21			a22				11				22				12	21			3	2
			Определителем матрицы А третьего порядка называется число,
найденное по формуле разложения определителя по первой строке:
						a11			a12			a13				a				a22			a23		a				a21		a23	a		a21	a22


				A		a			a			a
							21			22			23			11				a32			a33				12		a31		a33		13	a31	a32
							21			22			23			11				a32			a33				12		a31		a33		13	a31	a32
		1	3			a31			a32			a33
					1 5					4	5	3					4		1			2 1 0 5 2 4 0 5 3 3 4 2 1 3 50
	2
	2
	4	1	5	2					1
	3	2	0		2 0					3	0						3	2
	3	2	0			МИНОРЫ И АЛГЕБРАИЧЕСКИЕ ДОПОЛНЕНИЯ
						МИНОРЫ И АЛГЕБРАИЧЕСКИЕ ДОПОЛНЕНИЯ
			Минором						квадратной									матрицы									п-го				порядка			M ij	называется

определитель матрицы п–1-го порядка, полученной вычѐркиванием i-й строки и j-го столбца исходной матрицы.

				2	1	3
										1	3	1,
Пусть дана матрица A				4	1	5		. Тогда M 21		1	3	1,
				3	2	0				2	0
				3	2	0
M 32		3	22		, M 33		2 1		6 .
M 32	2	3	22		, M 33		2 1		6 .
	4	5					4 1

Алгебраическим дополнением элемента aij								квадратной	матрицы
называется число A 1 i j M			ij	.
		ij	ij
Для той же матрицы А:			A		1 2 1 M	21	1,	A 1 3 2 M	32	22 ,
				21		21		32	32
A 1 3 3 M	33	6 .
33	33

ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЯ РАЗЛОЖЕНИЕМ ПО ЛЮБОЙ СТРОКЕ И ЛЮБОМУ СТОЛБЦУ

Определитель матрицы п-го порядка есть число, равное сумме произведений элементов любой выбранной строки или столбца на их

		n	n
алгебраические дополнения.	A	aij Aij		aij Aij .
алгебраические дополнения.	A	aij Aij		aij Aij .
		i 1	j 1

Разложим определитель матрицы А по третьей строке:

		1	3		1	3	2	2	3		2	1	3 5 3 2 10 12 0 50
	2

A	4	1	5	3						0

	3	2	0		1	5		4	5		4	1

ТРАНСПОНИРОВАНИЕ МАТРИЦ

Транспонированной по отношению к матрице А называется матрица AT , полученная из А записыванием элементов строк в столбцы и наоборот:

	1	6		1	2
A			AT		.
	2			6
	2	3		6	3

УМНОЖЕНИЕ МАТРИЦЫ НА ЧИСЛО И СЛОЖЕНИЕ МАТРИЦ Чтобы умножить матрицу на число нужно каждый еѐ элемент

умножить на это число.

Сумма матриц одинаковой размерности есть матрица той же размерности, элементы которой равны суммам соответствующих элементов суммируемых матриц.

2		1	4		2	4		2	12		6	16		8
2			3
	3	0		1	2		6	0		3	6		3	6

УМНОЖЕНИЕ МАТРИЦ Действие выполнимо, если количество столбцов матрицы слева совпадает

с количеством строк матрицы справа: An p Bp m Cn m , в результате

получается матрица, у которой строк столько сколько у матрицы слева, а столбцов столько сколько у матрицы справа. Каждый элемент cij итоговой

матрицы равен сумме произведений одноимѐнных элементов i-й строки матрицы слева и j-го столбца матрицы справа:

									5
1		2	3	2	1	1 2 2 3 3 1 1 1 2 1 3 4				1		15
1		2	3	3		1 2 2 3 3 1 1 1 2 1 3 4				1		15
				3	1			2	5 3 1 1 0 1 5 1 1 4			9
	0	5	1				0	2	5 3 1 1 0 1 5 1 1 4		14	9
				1	4
				1	4

ОБРАТНЫЕ МАТРИЦЫ

Матрица A 1 называется обратной по отношению к квадратной матрице

А если выполняется соотношение A 1 A A A 1 E , где Е – единичная матрица – квадратная матрица на главной диагонали которой 1, а остальные элементы равны 0.

Обратные матрицы есть только у невырожденных матриц (чей определитель не равен 0).

							A	A	A
	1		T		T		11	21	31
A 1	1		A*	, где A*		A12		A22	A32
		A


							A13	A23	A33				3
											2	1	3

Найдѐм обратную			матрицу		по	отношению			к	A	4	1	5	.
											3	2	0
											3	2	0

A	50 0				A 1 существует.
A	50 0				A 1 существует.
A				1		5		10	, A		4	5	15 ,			A					4		1	5 ,				A						1	3			6 ,
A				1		5		10	, A		4	5	15 ,			A					4		1	5 ,				A						1	3			6 ,
11				2 0					12		3 0					13					3		2							21				2 0
				2 0							3 0										3		2											2 0
					3		9 ,			2		1							1				3		2 ,								2		3		22 ,
A		2			3		9 ,		A	2		1	7 ,			A			1				3		2 ,		A						2		3		22 ,
22			3		0				23	3		2				31				1			5						32				4		5
			3		0					3		2								1			5										4		5
																1
												A			2	1		6 .
												33			4	1
															4	1
																													10			6				2

						10 6			2								10					6	2						50			50			50
						10 6			2								10					6	2						50			50			50
				T										1															15			9					22
	A*					15 9			22			A 1		1			15 9						22						15			9					22	.
	A*					15 9			22			A 1					15 9						22															.
						5 7			6					50			5 7						6						50			50				50
						5 7			6								5 7						6							5		7				6

																														50		50				50
																														50		50				50
																			10 6							2		2 1							3
	Проверим по определению: A 1 A																1
																	1					15	9			22					4		1		5
																						15	9			22					4		1		5
																50						5 7				6					3	2			0
																						5 7				6					3	2			0

															6
					10 2 6 4 2 3								10 1 6 1 2 2																	10 3 6 5 2 0
	1			15 2 9 4 22 3								15 1 9 1 22 2																	15 3 9 5 22 0
	1

50				5 2 7 4 6 3								5 1 7 1 6 2																	5 3					7 5 6 0
				5 2 7 4 6 3								5 1 7 1 6 2																	5 3					7 5 6 0
												50	0		0				1		0	0
									1
									1			0 50 0							0 1			0		E .
												0 50 0							0 1			0		E .
									50			0	0		50				0		0	1
												0	0		50				0		0	1
	РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
			Общий вид системы линейных алгебраических уравнений из п уравнений
																		a11x1 a12 x2											... a1n xn					b1
																						a22 x2							... a2n xn b2
																		a21x1				a22 x2							... a2n xn b2
с		п			неизвестными					имеет				вид:				..........................................																	, где

																		a		n1	x	a	n2		x		2		... a		nn	x	n	b
																				n1	1		n2				2				nn		n	n
		a			a		...	a																		b
				11	12			1n																					1
A		a21			a22 ...			a2n		– матрица системы,												B				b2
A			... ... ... ...							– матрица системы,												B						...		– вектор-столбец
			... ... ... ...																									...

					an2 ...
		an1			an2 ...			ann																		bn
															x
															1
свободных						членов		системы,					X		x2			–			вектор-столбец											неизвестных.
свободных						членов		системы,					X					–			вектор-столбец											неизвестных.

															...

															xn
Определитель матрицы системы																A	называется главным определителем
Определитель матрицы системы																A	называется главным определителем
системы. Определитель											j		получается					из			главного								заменой j-го столбца
вектор-столбцом свободных членов системы В ( j 1,2,...,n ).

Для систем линейных алгебраических уравнений возможны следующие ситуации: система имеет единственное решение, система имеет бесконечное множество решений, система не имеет решений.

ПРАВИЛО КРАМЕРА

Если главный определитель

системы

0 , то система имеет

единственное решение, которое находится по формулам:

, x

,…, x

3x 2 y z 5

методом Крамера.

Решим систему x y z

4x y 5z 3

																														7
		,
							2	1						1				1							1 1									1			1			3 4 2 9 1 5 11 0.
			3
			3
			1 1					1			3										2									1
			4				1	5					1				5								4		5							4				1
			4				1	5
							2	1							1			1								0		1							0		1				5 4 2 3 1 3 11;
				5
				5
	1			0 1				1				5										2									1
	1														1		5									3	5								3				1
				3			1	5							1		5									3	5								3				1
				3			1	5
							5	1					0			1							1			1							1			0
						3
						3
2						1 0		1		3										5									1										3 3 5 9 1 3 33;
						4	3	5					3				5						4				5						4			3
						4	3	5
							2	5						1			0							1		0						1				1			3 3 2 3 5 5 22 .
					3				3										2									5
					3
	3				1 1			0
	3												1				3							4	3							4			1
					4		1	3					1				3							4	3							4			1
					4		1	3																												3, z 3
								x 1						11				1,						y			2 33															22 2 .
								x 1										1,						y			2 33															22 2 .
															11																	11										11
																											3 1							2 3 2 5
																	Проверка:													3 2 0
																	Проверка:										1			3 2 0

																											4 1 3 5 2 3
						Если главный определитель системы 0 , то система либо имеет
бесконечное множество решений, если 1																																				2 ... n						0 ; либо не имеет
решений, если хотя бы один из определителей j 0 , j																																										1,2,...,n .

МАТРИЧНЫЙ МЕТОД Матричная форма записи системы линейных алгебраических уравнений

имеет вид: AX B . Если 0 , у матрицы системы А существует обратная A 1

и справедливо равенство: X A 1B . То есть, чтобы решить систему матричным методом нужно найти обратную матрицу к матрице А и умножить еѐ на вектор-столбец свободных членов системы В.

																		3		2	1

Решим	ту		же		систему		матричным				методом.						A	1		1	1 ,	A		11 0
																		4		1
																		4		1	5
A 1		1		A* T .
		A


A		1			4 ,	A		1	1	9	, A	11		5	,	A	2 1		11,		A		3	1	11,
A	1	1			4 ,	A		1	1	9	, A	11		5	,	A	2 1		11,		A		3	1	11,
11	1		5			12		4	5		13	4	1			21	1 5				22		4	5

A	3 2				11, A						2	1		3 ,				A				3 1				4 ,	A		3	2	1.
23	4	1							31		1	1							32				1 1				33		1 1
	4	1									1	1											1 1						1 1
						4			11			3												4		11	3
			T																	1
	A*						9		11			4			A 1					1					9	11	4	.
	A*						9		11			4			A 1					11					9	11	4	.
							5		11			1								11					5	11	1
							5		11			1													5	11	1
								4		11 3 5											4 5					11 0		3 3
X A 1B				1															1					9
				1				9		11			4				0		1							5 11 0		4 3
								9		11			4				0									5 11 0		4 3
			11					5		11		1					3		11					5		5 11 0 1 3
								5		11		1					3							5		5 11 0 1 3
															11				1
												1
												1				33				3	.
																33				3	.
												11				22				2
																22				2

ВЕКТОРНАЯ АЛГЕБРА В R3

Вектором в R3 называется направленный отрезок, характеризующийся длиной и направлением.

z	Вектор	задаѐтся		координатами –			проекциями
	вектора на координатные оси. Пусть вектор a							имеет
a3				a
a			a	1
a	координаты		a	a2	. Его	длина	есть корень
	a2 у
				a3
	квадратный		из	суммы		квадратов	координат:
	квадратный		из	суммы		квадратов	координат:
	a a2	a2	a2	.	Направление		вектора	a
	1	2	3

определяется углами, которые он образует с осями координат. Косинусы этих углов называются направляющими косинусами вектора a и связаны с координатами соотношениями:

cos

, cos

; cos2 cos2 cos2 1.

Два вектора, имеющие одинаковое направление и одинаковую длину

называются равными.

ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ, БАЗИС

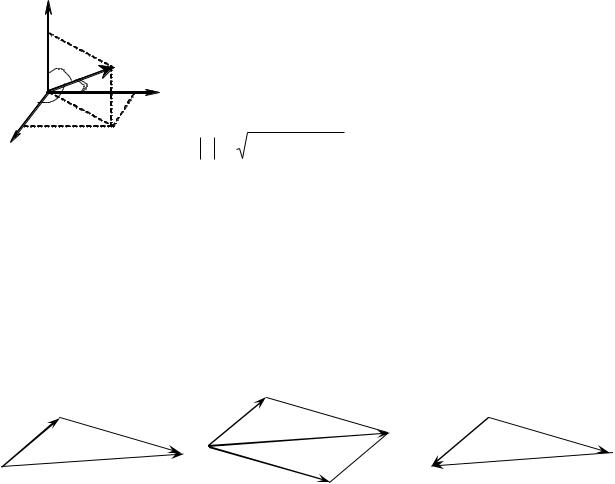
правило параллелограмма

правило треугольника

разность векторов

Векторы, лежащие на параллельных прямых или на одной прямой называются коллинеарными. При умножении вектора на число получаются

коллинеарные векторы: a b a || b .

Условие коллинеарности векторов: a || b a1 a2 a3 . b1 b2 b3

Линейной комбинацией векторов системы называется вектор, полученный в результате линейных операций над векторами системы.

Например, вектор d 1a 2b 3c , где 1 , 2 , 3 R , является линейной комбинацией системы векторов a , b и c .

Если ни один из заданных векторов системы не является линейной комбинацией остальных, то эти векторы называются линейно независимыми

(ЛНЗ).

Система трѐх векторов a , b и c в пространстве R3 линейно независима определитель, составленный из координат векторов системы не равен 0:

	a1	b1	c1
				0 a,		, c ЛНЗ
	a2	b2	c2	0 a,	b	, c ЛНЗ
	a3	b3	c3
Любая линейно независимая система из трѐх векторов образует базис

пространства R3 , то есть любой вектор пространства можно представить в виде линейной комбинации базисных векторов. Это представление называется

разложением вектора по базису, а коэффициенты разложения –

координатами вектора в данном базисе.

Например, если

система векторов a ,

b и c образует базис пространства

R3 , то представление

является разложением вектора d по

базису a , b и c , а 1 , 2 , 3 R – его координаты в этом базисе, определяются

a				b			c			d
	1	1		1	2		1	3			1
из системы уравнений: a2 1 b2 2							c2 3			d2 .
a			1	b		2	c		3	d		3
	3		1	3		2	3		3			3
														1					0
Естественный базис пространства R3
Естественный базис пространства R3													– векторы i		0	,	j	1		и
															0				0
															0				0

k 0 , так как коэффициенты разложения вектора по этому базису совпадают

10
	a
с координатами вектора в пространстве R3 :	1
	1
	a a2	a a1i	a2	j a3k .

	a3

СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

	a
	1
Скалярным произведением векторов	a a2	и

	a3

b b2 называется

число, равное сумме произведений одноимѐнных координат:

a b a1b1 a2b2 a3b3 .

Скалярное произведение векторов численно равно произведению их длин на косинус угла между ними: a b a b cos , где 0 .

Геометрическое приложение: скалярное произведение применяется для

вычисления углов между векторами: cos a b , где – угол между a и b . a b

Свойства скалярного произведения:

a a

2 , a

c a

a c,

;

i 1, j j 1, k k 1, i j 0 , i

k 0 ,

j k 0 .

0 a

Условие ортогональности векторов:

ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

Векторным произведением векторов

b b2

называется

вектор, найденный по формуле:

Векторное произведение векторов a и b есть вектор c : длина которого

численно равна площади параллелограмма,

построенного на векторах a и b

sin ;

как на сторонах

перпендикулярный плоскости векторов a

c a, c

направленный

так,

что

если смотреть

из

его конца

на

a и

плоскость векторов

b ,

то кратчайший поворот от

b происходит

против часовой стрелки.

Геометрическое приложение: векторное произведение применяется при

1 / 21 2 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
18.08.201947.74 Кб4Marketing_innovatsy111.docx
#
29.03.20162.49 Mб25Mark_Salem_Kak_chitat_cheloveka.pdf
#
12.06.2015640.3 Кб5Martynovich_1.pdf
#
12.06.2015443.12 Кб4Maslennikov_TV-524 (10).pdf
#
20.09.2019167.31 Кб10matan.docx
#
12.06.2015659.01 Кб4Matematika_Gorodskoy_kadastr_Logistika_1_chas.pdf
#
20.04.201995.23 Кб1Materialy_k_ekzamenu_1.doc
#
11.06.2015851.46 Кб111Metoda_MG_OBSCHIE_SVEDENIYA_kniga.doc
#
11.06.20151.62 Mб10Metodicheskie_ukazania_k_lab_rab__10.doc
#
11.06.2015229.89 Кб20Metodicheskie_ukazania_k_lab_rab__64.doc
#
11.06.2015159.23 Кб6Metodicheskie_ukazania_k_lab_rab__68-1.doc