
Matematika_Gorodskoy_kadastr_Logistika_1_chas
.pdf
11
вычислении площади параллелограмма и треугольника Sпарал ABCD AB AC ,
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
S ABC |
|
AB AC |
|
и при нахождении вектора ортогонального двум заданным. |
||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Свойства векторного произведения: |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
a a 0, |
|
a |
|
|
|
|
|
a, a |
|
c a |
|
a c, a |
|
a |
|
a |
|
; |
||||||||||||||||||||||||||||||||||||
|
b |
b |
b |
b |
b |
b |
b |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
i 0 , |
j |
|
j |
0, k k 0 , i j k , |
j k i , k i j . |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
a |
|
0 a |
|
|
; |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Признак коллинеарности векторов: |
b |
|
|
b |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
a |
|
|
1 |
|
|
Смешанным произведением векторов a a2 |
|
, |
|
|
|
a3 |
|
|
b1
b b2 иb3
c1 c c2c3
называется число, равное скалярному произведению вектора a |
на векторное |
||||||||||||
|
|
и c : a |
|
c a |
|
c . |
|
|
|
|
|||
произведение векторов |
b |
b |
b |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
a1 |
b1 |
c1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Расчѐтная формула: a |
|
c |
a2 |
|
|
|
|
||||||
b |
b2 |
c2 |
. |
|
|||||||||
|
|
|
|
|
|
|
|
|
a3 |
b3 |
c3 |
|
|
Модуль смешанного произведения векторов |
численно |
равен объѐму |
|||||||||||
параллелепипеда, построенного на векторах a , b и c как на рѐбрах.
Геометрическое приложение: смешанное произведение применяется для вычисления объѐма параллелепипеда и треугольной пирамиды
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
V |
|
AB AC AD |
, V |
ABCD |
|
|
|
AB AC AD |
. |
|||||||||||||
|
||||||||||||||||||||||
парал да |
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Вектора a , b и c компланарны, если они лежат в одной плоскости.
Условие компланарности векторов: a , b и c компланарны a b c 0 .
|
УРАВНЕНИЯ ПЛОСКОСТИ В R3 . |
|
||
|
Пусть |
M x, y, z |
– текущая точка плоскости |
|
n |
α. |
Точка |
A a1, a2 , a3 . |
Вектор |
|
n |
|
|
|
|
|
А |
1 |
|
|
|
|
|
n n2 |
|
называется |
нормалью |
к |
||
М |
||||||
|
|
|
|
|
||
α |
n3 |
|
|
|
|
плоскости α. Тогда плоскость α можно
описать уравнением:
: n1 x a1 n2 y a2 n3 z a3 0 – уравнение плоскости, проходящей через заданную точку с заданным вектором нормали.

12
А |
М
α
Пусть |
M x, y, z – текущая точка плоскости |
||||||
α. Точка A a1, a2 , a3 . |
Векторы |
и |
|||||
неколлинеарны между собой и || , |
|| . |
||||||
Тогда |
плоскость |
α |
можно |
описать |
|||
|
|
x a1 |
1 |
1 |
|
|
|
|
|
|
|
||||
уравнением: : |
y a2 |
3 |
2 |
|
0 – |
|
|
|
|
z a3 |
3 |
3 |
|
|
|
уравнение плоскости, проходящей через заданную точку параллельно двум неколлинеарным векторам.
В частности, уравнение плоскости, проходящей через три точки M1 x1, y1, z1 ,
M 2 x2 , y2 , z2 и M3 x3 , y3 , z3 имеет вид: : |
|
x x1 |
x2 x1 |
x3 x1 |
|
|
|
||||
|
y y2 |
y2 y1 |
y3 y1 |
0 . |
|
|
|
z z3 |
z2 z1 |
z3 z1 |
|
Оба типа уравнений плоскости после преобразований приобретают вид:
: Ax By Cz D 0 – общее уравнение плоскости,
где числа A, B, C – координаты вектора нормали одновременно не равные нулю.
УРАВНЕНИЯ ПРЯМОЙ В R3 .
|
s |
|
Пусть |
M x, y, z |
– текущая точка прямой l. Точка |
||
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
s |
|
М |
|
l |
A a1 |
, a2 , a3 l . |
1 |
|
|
|
Вектор s s 2 |
|| l называется |
|||||
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s3 |
|
направляющим вектором прямой l. Тогда прямую l можно описать
уравнениями: l : |
x a1 |
|
|
y a2 |
|
z a3 |
– канонические уравнения или |
|
||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
s1 |
|
|
|
|
|
|
s2 |
|
|
s3 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
x a1 s1t |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t R – параметрические уравнения. |
|
|||||||||||
|
|
|
|
|
l : y a2 s2t, |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
a3 s3t |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
В |
частности, |
|
|
|
уравнения прямой, |
проходящей |
через две |
точки |
||||||||||||||||||
M |
|
x , y , z |
и M |
|
x |
|
, |
y |
|
, z |
|
имеют вид: l : |
|
x x1 |
|
y y1 |
|
z z1 |
. |
|
||||||||
1 |
2 |
2 |
2 |
2 |
|
|
|
|
|
|||||||||||||||||||
|
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 x1 |
|
y2 y1 |
|
z2 z1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
у |
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
УРАВНЕНИЯ ПРЯМОЙ В R2 . |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
n |
|
|
|
|
|
А |
|
|
|
l |
|
|
|
Пусть M x, y |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– текущая точка прямой l. Точка |
||||||||||||||
|
|
|
|
М |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A a1, a2 l . Тогда |
|
|
|
|
|
|
||||||
|
|
|
|
φ |
|
|
|
|
|
|
|
|
|
|
|
|
прямую |
l можно |
описать |
|||||||||
х
13
уравнениями трѐх типов, в зависимости от других данных.
1. |
Пусть известны координаты вектора |
n |
|
l |
– нормали прямой l. |
|||||
n 1 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n2 |
|
|
x a1 n2 y a2 0 . |
|
|
Тогда соответствующее уравнение имеет вид: l : n1 |
|||||||||
2. |
Если задан вектор |
s |
|
|| l |
– направляющий |
|
вектор прямой l, то |
|||
s 1 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
s2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x a |
y a |
2 |
x a1 |
s1t |
|
||
прямую описывают уравнения: l : |
1 |
|
|
и l : |
|
, t R . |
|||||||||||
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
s1 |
s2 |
|
y a2 |
s2t |
|
||
В частности, уравнение прямой, проходящей через две точки M1 x1, y1 и |
|||||||||||||||||
M |
|
x |
|
, y |
|
имеет вид: l : |
x x1 |
|
|
y y1 |
. |
|
|
|
|
|
|
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
x2 x1 |
y2 y1 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3. Если известен угловой коэффициент прямой k tg , то уравнение прямой с угловым коэффициентом имеет вид: l : y a2 k x a1 .
Нетрудно установить связь между угловым коэффициентом и
координатами векторов нормали и направляющим: k n1 s2 . n2 s1
Все типы уравнений прямой после преобразований приобретают вид: l : Ax By C 0 – общее уравнение прямой,
где числа A, B – координаты вектора нормали одновременно не равные нулю.
КРИВЫЕ ВТОРОГО ПОРЯДКА
|
y |
|
|
|
|
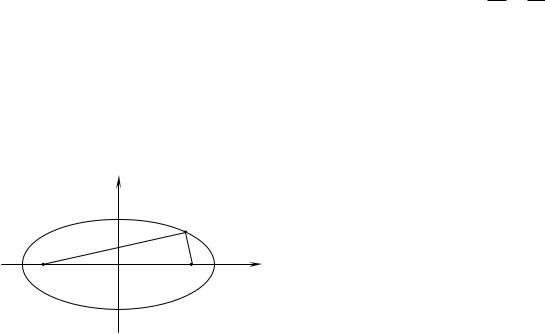
Эллипсом с фокусами F1 и F2 |
называется |
|||||
|
b |
|
|
геометрическое |
место |
точек |
M данной |
|||||
|
M(x,y) |
плоскости, |
отличных от точек F1 и |
F2 , и таких, |
||||||||
|
|
|||||||||||
|
|
|
|
|||||||||
|
|
|
|
что сумма расстояний от |
M до обоих фокусов |
|||||||
F2(-c,0) |
|
F1(c,0) |
a |
x постоянна и равна 2a (a 0) . |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
x2 |
|
y2 |
1 |
– каноническое уравнение эллипса с |
|||
|
|
|
|
|
a2 |
|
||||||
|
|
|
|
|
|
b2 |
|
|
|
|
||
|
|
|
|
полуосями длины |
a и b , |
получаемое в случае, |
||||||
когда фокусы эллипса расположены на оси Ох симметрично относительно начала координат и при этом a b 0 .
Точки пересечения эллипса с координатными осями называются вершинами эллипса, а отрезки, заключѐнные между вершинами, называются осями эллипса: большая (фокальная) ось длиной 2a и малая ось длиной 2b . Оси координат являются осями симметрии эллипса, а начало координат — его центром симметрии. Для такого эллипса справедливы следующие
соотношения: |
c2 a2 b2 ; |
|
c |
1 |
– его эксцентриситет; |
x |
a |
– его |
|
a |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
||
директрисы; r1 |
|
MF1 |
|
a x и r2 |
|
|
MF2 |
|
a x – фокальные радиусы точек |
|
|
|
|
||||||
эллипса. |
|
|
|
|
|
|
|
||
Если b a 0 , |
|
то фокусы |
эллипса лежат на оси Оу симметрично |
||||||
относительно начала координат, а его каноническое уравнение имеет тот же вид, причѐм большая (фокальная) ось длиной 2b и малая ось длиной 2a . При
этом справедливы соотношения: c2 b2 a2 ; bc 1 – его эксцентриситет; y b – его директрисы.
Если a b , то получаем уравнение окружности x2 y2 a2 с центром в начале координат радиусом а. Эксцентриситет окружности 0 .
Из школьного курса известно, что окружность с центром в точке A x0 , y0
и радиусом R можно задать уравнением x x0 2 y y0 2 R2 .
|
y |
|
|
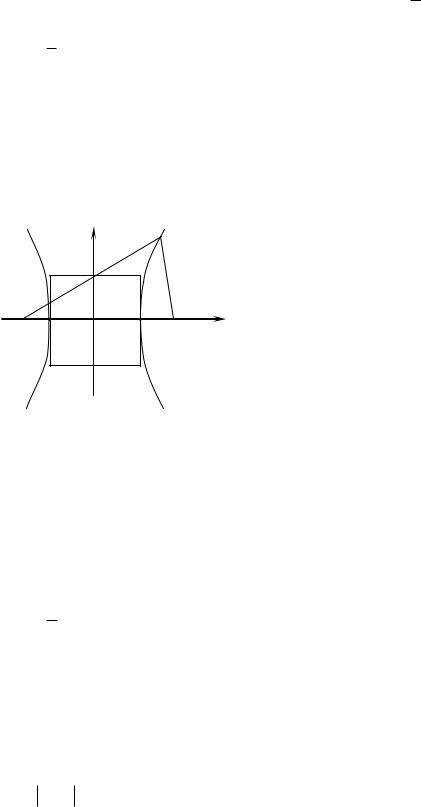
Гиперболой с фокусами F1 и F2 называется |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
b |
геометрическое место точек M данной плоскости, |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
отличных |
от точек |
F1 и |
F2 таких, что |
модуль |
||||
|
|
разности |
расстояний |
от |
M до обоих |
фокусов |
||||
F2(-c,0) |
O |
a F1(c,0) x постоянен и равен 2a (a 0) . |
|
|||||||
|
|
|
x2 |
|
y2 |
1 – каноническое уравнение гиперболы с |
||||
|
|
|
a2 |
|
||||||
|
|
|
|
b2 |
|
|
|
|
||
|
|
полуосями длины a |
и b , получаемое в случае, |
|||||||
когда фокусы эллипса расположены на оси Ох симметрично относительно начала координат.
Точки пересечения ( a,0) и ( a,0) гиперболы с осью Ox называются
вершинами гиперболы, а величина a — действительной полуосью. Точки (0, b) и (0,b) называются мнимыми вершинами гиперболы, а величина b —
мнимой полуосью. Прямоугольник с центром в начале координат и со сторонами, параллельными координатным осям и проходящими через вершины параболы, называется основным прямоугольником гиперболы. Его диагонали
y ba x являются асимптотами гиперболы. Оси координат являются осями
симметрии гиперболы, а начало координат — еѐ центром симметрии. Если a b, то гипербола называется равносторонней. Для такой гиперболы
справедливы следующие соотношения: c2 a2 |
b2 ; |
|
|
c |
1 |
– |
еѐ |
||||||||
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
a |
|
|
|
|||
эксцентриситет; |
x |
a |
– |
еѐ |
директрисы; |
r |
|
MF |
|
|
x a |
и |
|||
|
|
||||||||||||||
|
|||||||||||||||
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
r2 MF2 a x – фокальные радиусы точек правой ветви гиперболы.

15
Если фокусы лежат на оси Оу симметрично относительно начала
координат, то уравнение гиперболы имеет вид |
x2 |
|
|
y2 |
1 . При этом точки |
|
a2 |
b2 |
|||||
|
|
|
||||
пересечения ( a,0) и ( a,0) гиперболы с осью |
Ox называются мнимыми |
|||||
вершинами гиперболы, а величина a — мнимой полуосью; точки (0, b) и (0,b) называются вершинами гиперболы, а величина b — действительной полуосью,
причѐм |
c |
1 |
– еѐ эксцентриситет; y |
b |
– еѐ директрисы. |
|||||||||
b |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Гиперболы |
|
x2 |
|
y2 |
1 и |
x2 |
|
y2 |
1 |
называются сопряжѐнными и |
||||
|
a2 |
b2 |
a2 |
b2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
имеют общий основной прямоугольник и асимптоты.
l |
y |
|
|
|
|
|
Пусть на плоскости задана прямая l и точка F , не |
||||||||
N |
|
M |
|
|
лежащая |
на |
этой |
прямой. |
Параболой |
называется |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
геометрическое |
место |
точек |
M |
плоскости, |
|||||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
равноудалѐнных |
от |
данной |
|
точки |
F (фокуса) и от |
|||||
p |
O |
p |
x |
|
данной прямой l (директрисы). |
|
|
||||||||
2 |
|
F |
, 0 |
|
y |
2 |
2 px ( p 0) |
|
– каноническое уравнение |
параболы, |
|||||
|
2 |
|
|
|
|
||||||||||
если за ось абсцисс принять прямую, проходящую через фокус и перпендикулярную директрисе, а начало координат поместить посередине между фокусом и директрисой. Парабола
имеет одну ось симметрии, которая при указанном выше выборе системы координат совпадает с осью Ox , Точка O является вершиной параболы.
Эксцентриситет параболы 1, еѐ директриса |
x |
p |
, а |
r |
|
MF |
|
x |
p |
– |
|
|
|||||||||
|
|
|
|
|||||||
фокальный радиус еѐ точек. |
2 |
|
|
|
|
|
2 |
|
||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
Ветви параболы, заданной уравнением |
y2 2 px |
|
симметричны |
|||||||
относительно оси Ox , но направлены в отрицательную сторону этой оси. Уравнения x2 2 py и x2 2 py задают параболы, ветви которых симметричны относительно оси Oy и имеют в первом случае положительное, а во втором – отрицательное направления.
Полярное уравнение кривой второго порядка
Если полюс пометить в фокус кривой второго порядка, а полярную ось направить в сторону, противоположную от ближайшей вершины, то все виды
кривых второго порядка имеют полярное уравнение вида |
p |
, где для |
|
||
1 cos |
центральных кривых значение параметра p b2 . a
16
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
1.Самарин Ю.П., Сахабиева Г.А., Сахабиев В.А. Высшая математика: учеб. пособие. – М.: Машиностроение, 2006.
2.Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. – М.: Оникс, Мир и образование, 2005.
3.Сборник задач по математике для втузов. Линейная алгебра и основы математического анализа / под ред. А. В. Ефимова, Б. П. Демидовича. –
М.: Наука, 1979.
4.Проскуряков И.В. Сборник задач по линейной алгебре. – М.: Наука, 1966.
5.Клетеник Д.В. Сборник задач по аналитической геометрии. – М.: Наука,
1998.
6.Линейная алгебра и элементы аналитической геометрии: методические указания для студентов очной и заочной форм обучения / Авторский коллектив кафедры ПМиВТ РГСУ. – Ростов н/Д: РГСУ, 2011.
