
- •Введение.
- •Общее введение в теорию игр.
- •Биматричные игры.
- •Оптимальность по Парето
- •Равновесие по Нэшу
- •6. Решение биматричных игр
- •7. Биматричные игры 2х2 и их решение.
- •7.1. «Семейный спор»
- •7.2. «Два бандита»
- •«Зачет»
- •8. Почти антагонистические игры.
- •8.1. «Борьба за рынки»
- •9. Заключение
- •10. Список литературы
- •16 7. Биматричные игры 2х2 и их решение.
6. Решение биматричных игр
Иногда анализ 2 X 2-матричных игр проводится путем составления точного описания множеств ситуаций, приемлемых для каждо- го из игроков (это описание проводится на геометрическом языке, но, очевидно, может быть представлено и в чисто алгебраическом виде), и нахождения пересечения этих двух множеств. В принципе этот способ описа- ния ситуаций равновесия может быть применен и к матрич- ным играм произвольного формата. Однако он пока еще не нашел достаточ- но наглядных средств выражения, которые сделали бы его конкурентоспо- собным среди других методов анализа матричных игр.
Вместе с тем, как мы сейчас увидим, применение способа описа- ния ситуаций равновесия к анализу биматричных игр и даже к нахождению их решений, правда, весьма неэффективному, представляется вполне целесообразным.
Пусть Г=Г(А,В)- m x n биматричная игра с матрицами выигрышей игроков:
(6)
Множество ζ1(Г) всех ситуаций, приемлемых для игрока 1 в этой игре, состоит из всех ситуаций (X, У), для которых выполняется система неравенств:
(7)
Далее я буду рассматривать случаи, соответствующие тому или иному спектру стратегии12 X.
Пусть .
Тогда в (7) для
.
Тогда в (7) для
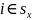 по
свойству дополняющей нежесткости13
должно выполняться точное равенство.
Отсюда следует, что для любых двух
смешанных стратегий X’
и
Х''
обладающих
одним и тем же спектром и дающих в паре
с одной и той же стратегией Y
приемлемые
ситуации
по
свойству дополняющей нежесткости13
должно выполняться точное равенство.
Отсюда следует, что для любых двух
смешанных стратегий X’
и
Х''
обладающих
одним и тем же спектром и дающих в паре
с одной и той же стратегией Y
приемлемые
ситуации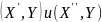 ,
должно быть X'AYT
= X»AYT.
,
должно быть X'AYT
= X»AYT.
Таким образом, на множестве X(sx) всех стратегий игрока 1 со спектром sx величина ХАYT не зависит от X.
Этот факт является для дальнейшего решающим.
Во-первых,
из него следует, что вместе с любой
приемлемой для игрока 1 ситуацией (X,Y)
таковой
же является любая ситуация (X’,
F),
где
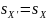 , т.е. ситуации входят (или не входят) в
ζ(Г) целыми «блоками» вида (X(s),
Y).
, т.е. ситуации входят (или не входят) в
ζ(Г) целыми «блоками» вида (X(s),
Y).
Во-вторых, отсюда же следует, что на X(sХ) выражение ХАYТ представляет собой единую линейную форму от Y, и на X(sx) система (7) оказывается системой именно линейных (а не билинейных) неравенств, и множество ее решений составляет выпуклый многогранник, который зависит опять-таки не от конкретной стратегии X, и лишь от ее спектра sx = s. Обозначим этот многогранник через ζ(s).
Попутно обратим внимание на то, что каждый из таких многогранников ζ(s) зависит только от матрицы А (и не зависит от матрицы В ). Значит, ситуации входят (или не входят) в ζ1(Г) целыми произведениями X(s) х ζ1(s). Иными словами,

Очевидно, число произведений в этом объединении не может превосходить 2m — 1 (s может быть любым непустым подмножеством х), а множество ζ1 ( Г ) зависит только от матрицы А. В силу тех же причин

где Y(t) — множество стратегий игрока 2, имеющих данный спектр t, а ζ2(t) - множество решений X системы неравенств
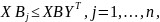 (8)
(8)
где supp Y = t (как и выше, решение зависит здесь не от самой стратегии у, а лишь от ее спектра). Здесь в объединение входит не более 2n — 1 произведений. Множество ζ2 (Г) определяется только матрицей В.
Окончательно мы получаем
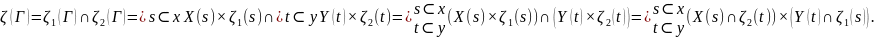 (9)
(9)
При
любом
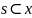 нахождение
многогранника ζ1(s)
состоит в решении системы линейных
неравенств, т.е. в выполнении конечного
числа рациональных (арифметических)
операций над элементами матрицы А.
Точно
так же выполнением конечного числа
рациональных операций над элементами
матрицы В
может
быть найдено множество
ζ2(t)
при
любом
нахождение
многогранника ζ1(s)
состоит в решении системы линейных
неравенств, т.е. в выполнении конечного
числа рациональных (арифметических)
операций над элементами матрицы А.
Точно
так же выполнением конечного числа
рациональных операций над элементами
матрицы В
может
быть найдено множество
ζ2(t)
при
любом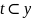 .
.
Следовательно,
таким же конечно-рациональным путем
находится каждое из пересечений
 и
и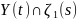 ,
и потому, в силу отмеченной конечности
множества вариантов для спектров s
и t
и согласно формуле (9), - и все множество
ζ(Г).
,
и потому, в силу отмеченной конечности
множества вариантов для спектров s
и t
и согласно формуле (9), - и все множество
ζ(Г).
Хотя при сколько-нибудь больших значениях чисел m и n описанная процедура нахождения приемлемых (а по ним – и равновесных) ситуаций в биматричной игре является весьма громоздкой, при m = n = 2 для спектров стратегий каждого игрока оказывается не более трех вариантов, и приведенный способ представляется реально выполнимым геометрически. Мы займемся этим в следующей части.
